Die Funktionen stellen Brüche dar, bei denen die Funktionsvariable auch im Nenner vorkommt. Das ist bei Polynomfunktionen nicht der Fall.
Die Zähler und Nenner der Funktionen enthalten Polynomfunktionen.
Eine rationale Funktion ist ein Quotient zweier Polynomfunktionen.
Hinweis: Da im Nenner einer rationalen Funktion die Polynomfunktion
Die Menge der rationalen Funktionen stellt also in analoger Weise eine Erweiterung der Menge der Polynomfunktionen dar, wie die Menge der rationalen Zahlen (= Bruchzahlen) eine Erweiterung der Menge der ganzen Zahlen darstellt. Deshalb werden Polynomfunktionen auch als „ganz-rationale Funktionen“ bezeichnet.
achsensymmetrisch, wenn f(–x) = f(x)
punktsymmetrisch, wenn f(–x) = – f(x)
5.
f (–x) =
(–x) =  = –
= –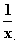 = –f
= –f (x)
(x) 
Der Graf von f ist punktsymmetrisch bzgl. des Koordinatenursprungs.
ist punktsymmetrisch bzgl. des Koordinatenursprungs.
f (–x) =
(–x) =  = –
= –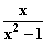 = –f
= –f (x)
(x) 
Der Graf von f ist punktsymmetrisch bzgl. des Koordinatenursprungs.
ist punktsymmetrisch bzgl. des Koordinatenursprungs.
f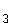 (–x) =
(–x) =  =
= 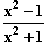 = f
= f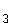 (x)
(x) 
Der Graf von f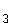 ist achsensymmetrisch bzgl. der y-Achse.
ist achsensymmetrisch bzgl. der y-Achse.
f (–x) =
(–x) =  =
=  = –
= – ≠ ± f
≠ ± f (x)
(x) 
Der Graf von f ist bzgl. des Koordinatensystems nicht symmetrisch.
ist bzgl. des Koordinatensystems nicht symmetrisch.
Eine rationale Funktion hat einen zur y-Achse achsensymmetrischen Grafen, wenn das Zähler- und das Nennerpolynom gleichartiges Symmetrieverhalten zeigen, also beide achsensymmetrische oder beide punktsymmetrische Grafen besitzen.
Eine rationale Funktion hat einen zum Ursprung punktsymmetrischen Grafen, wenn das Zähler- und das Nennerpolynom ungleichartiges Symmetrieverhalten zeigen, also eine von ihnen einen achsensymmetrischen und die andere einen punktsymmetrischen Grafen besitzt.
Umkehrschluss:
Wenn das Zähler- oder das Nennerpolynom einen nicht symmetrischen Grafen hat, ist auch der Graf der rationalen Funktion nicht symmetrisch.
Beurteilung der Gültigkeit dieser Aussage:
Die Aussage gilt nur, wenn das „oder“ im Sinne des strengen „entweder oder“ interpretiert wird; im Falle der toleranteren „oder auch“-Interpretation gilt sie nicht, wie das folgende Gegenbeispiel zeigt:
f(x) =  =
=  = x
= x
Obwohl in diesem Fall weder das Zähler- noch das Nennerpolynom einen symmetrischen Grafen besitzt, ist der Graf der rationalen Funktion f achsensymmetrisch bzgl. der y-Achse.
Die Menge aller z. B. reellen Zahlen, die die Funktionsvariable annehmen kann, so dass sich damit ein definierter Funktionswert ergibt.
Da der Nenner variabel ist, kann er u. U. auch null werden, so dass der Funktionswert dann nicht definiert ist.
10.
f (x) =
(x) = 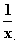
n(x) = 0  x = 0
x = 0  ID
ID = IR \ {0}.
= IR \ {0}.
f (x) =
(x) = 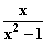
n(x) = 0 
 – 1 = 0
– 1 = 0 


 = ±1
= ±1 
 = IR \ {–1; 1}.
= IR \ {–1; 1}.
f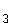 (x) =
(x) = 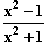
n(x) = 0 
 + 1 = 0
+ 1 = 0 

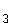 = IR.
= IR.
f (x) =
(x) = 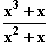
n(x) = 0 
 + x = 0
+ x = 0 

 = 0; x
= 0; x = –1
= –1 
 = IR \ {–1; 0}.
= IR \ {–1; 0}.
11.3
z. B. f(x) = 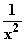
Allgemein muss der Exponent im Nenner gerade sein, d. h.
12.2
z. B. f(x) =  =
= 
Allgemein müssen die Exponenten der Linearfaktoren im Nenner gerade sein, d. h. es müssen Polstellen mit gerader Vielfachheit vorliegen.
13.1
Skizze für den Nenner: 
 –1
–1 
 (x) =
(x) = 

 ∞
∞
x = –1 ist also eine Polstelle von f , und zwar eine mit Vorzeichenwechsel.
, und zwar eine mit Vorzeichenwechsel.
13.3
 (x) =
(x) =  =
= 
 0
0 
 (x) =
(x) = 
 1
1
Wenn der Zähler null, der Nenner jedoch ungleich null ist.
15.
Nullstellen von f (x) =
(x) = 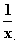 : Keine, da der Zähler nicht null werden kann.
: Keine, da der Zähler nicht null werden kann.
Nullstelle von f (x) =
(x) = 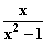 : x = 0
: x = 0
Nullstellen von f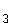 (x) =
(x) = 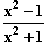 :
:
x – 1 = 0
– 1 = 0  x
x = 1
= 1  x
x

 = ± 1
= ± 1
Nullstellen von f (x) =
(x) = 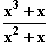 :
:
x + x = 0
+ x = 0  x(x
x(x + 1) = 0
+ 1) = 0  x = 0
x = 0
Da aber der Nenner bei  , sondern eine Definitionslücke, nämlich nach 13.3 eine hebbare Lücke.
, sondern eine Definitionslücke, nämlich nach 13.3 eine hebbare Lücke.
Skizze des Grafen von f1:

Gleichungen der Asymptoten des Grafen von f1:
x = 0 (senkrechte Asymptote)
y = 0 (waagrechte Asymptote)
Skizze des Grafen von f2:

Gleichungen der Asymptoten des Grafen von f2:
x = –1; x = 1 (senkrechte Asymptoten)
y = 0 (waagrechte Asymptote)
Skizze des Grafen von f3:

Gleichungen der Asymptote des Grafen von f3:
empirisch:
y = 1 (waagrechte Asymptote)
Skizze des Grafen von f4:

Gleichungen der Asymptoten des Grafen von f4:
x = –1 (senkrechte Asymptote)
empirisch:
y = x – 1 (schiefe Asymptote)
Bei der Ermittlung der nicht senkrechten Asymptote wird das asymptotische Verhalten (Anschmiegeverhalten) des Grafen für  ± ∞
± ∞
Also liegt eine waagrechte Asymptote mit der Gleichung
18.3
x  ± ∞
± ∞  f
f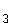 (x) =
(x) = 
 1
1
Polynomdivision von f4:
(Es genügt, den gekürzten Funktionsterm zu verwenden!)

Für x  ± ∞ strebt der echt gebrochen-rationale Anteil gegen null
± ∞ strebt der echt gebrochen-rationale Anteil gegen null
 Gleichung der schiefen Asymptote:
Gleichung der schiefen Asymptote:
Ist der Zählergrad mindestens so groß wie der Nennergrad, so gilt:
| Asymptotengrad = Zählergrad – Nennergrad |
f(x) = x3; g(x) = x2 + 1
Nach der Produktregel ergibt sich die Ableitung
(f(x) · g(x))' = 3x2 · (x2 + 1) + x3 · 2x
= 3x4 + 3x2 + 2x4
= 5x4 + 3x2
Mit elementarer Rechnung ergibt sich
f(x) · g(x) = x5 + x3 
(f(x) · g(x))' = 5x4 + 3x2
Die Produktregel liefert also das selbe Resultat wie eine elementare Rechnung.
f(x) = (x3 – x)2
Nach der Kettenregel ergibt sich die Ableitung
f '(x) = 2(x3 – x) · (3x2 – 1)
= 6x5 – 2x3 – 6x3 + 2x
= 6x5 – 8x3 + 2x
Mit elementarer Rechnung ergibt sich
f(x) = x6 – 2x4 + x2 
f '(x) = 6x5 – 8x3 +2x
Die Kettenregel liefert also das selbe Resultat wie eine elementare Rechnung.
Sei n 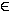 IN. Dann gilt:
IN. Dann gilt:

 , w. z. b. w.
, w. z. b. w.
a) f(x) = 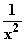 =
= 
 f '(x) = –2
f '(x) = –2 = –
= –
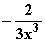 =
= 

 f '(x) = 2
f '(x) = 2 =
=  c) f(x) =
c) f(x) = 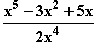 =
= 
 f '(x) =
f '(x) =  =
= 
( =
 )
)
24.
f(x) = 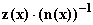

f '(x) = 
=  =
= 
an den Extremstellen, also den Nullstellen der ersten Ableitung mit ungerader Vielfachheit
an den Extremstellen und an den Polstellen mit gerader Vielfachheit
f(x) = 1/x² : f steigt für x < 0 und fällt für x > 0.
an den Wendestellen, also den Nullstellen der zweiten Ableitung mit ungerader Vielfachheit
an den Wendestellen und an den Polstellen mit ungerader Vielfachheit
f(x) = 1/x : der Graf von f ist für x < 0 rechts- und für x > 0 linksgekrümmt.
27.1
27.2
f(x) = 

f '(x) = 
= 
=  , w. z. b. w.
, w. z. b. w.
28.
Monotonieverhalten von f (x) =
(x) = 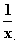 :
:
f '(x) =
'(x) = 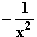 besitzt keine Nullstellen.
besitzt keine Nullstellen.
Für x < 0 wie auch für x > 0 ist f '(x) < 0
'(x) < 0 
Die Funktion f1 fällt in ihrer gesamten Definitionsmenge.
Monotonieverhalten von f (x) =
(x) = 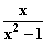 :
:
f '(x) =
'(x) =  =
=  = 0
= 0
 x2 = –1: keine Lösung.
x2 = –1: keine Lösung.
Da der Zähler immer und der Nenner nie negativ ist, ist  '(x)
'(x)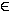 IR \ {–1;1}
IR \ {–1;1} in
in
Monotonieverhalten von f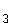 (x) =
(x) = 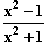 :
:
f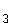 '(x) =
'(x) = 
=  =
=  = 0
= 0
 x = 0
x = 0
Monotonietabelle von f3 :
| x < | 0 | < x | |
|---|---|---|---|
| Zähler der Ableitungsfkt. | – | 0 | + |
| Nenner der Ableitungsfkt. | + | + | + |
| Steigung | – | 0 | + |
| Graf | fällt | TIP(0 | –1) | steigt |
Monotonieverhalten von f (x) =
(x) = 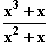 :
:
Wenn man die hebbare Lücke  verwenden.
verwenden.
f '(x) =
'(x) = 
=  =
=  = 0
= 0
 x
x + 2x – 1 = 0
+ 2x – 1 = 0 


 =
=  = –1 ±
= –1 ±
Monotonietabelle von f4 :
| x < | –1 – | < x < | –1 | < x < ≠ 0 | –1 + | < x | |
|---|---|---|---|---|---|---|---|
| Zähler der Ablfkt. | + | 0 | – | – | – | 0 | + |
| Nenner der Ablfkt. | + | + | + | + | + | + | + |
| Steigung | + | 0 | – | # | – | 0 | + |
| Graf | steigt | HOP (–1 –  |–2 – 2 |–2 – 2 ) ) | fällt | # | fällt | TIP (–1 +  |–2 + 2 |–2 + 2 ) ) | steigt |
29.
Krümmungsverhalten von f (x) =
(x) = 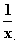 :
:
f '(x) =
'(x) = 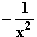 = –
= –
 f
f ''(x) = 2
''(x) = 2 =
=  besitzt keine Nullstellen.
besitzt keine Nullstellen.
Für x < 0 ist f ''(x) < 0 und für x > 0 ist f
''(x) < 0 und für x > 0 ist f ''(x) > 0
''(x) > 0 
Der Graf der Funktion f ist für
ist für
Krümmungsverhalten von f (x) =
(x) = 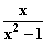 :
:
f '(x) =
'(x) = 
 f
f ''(x) =
''(x) = 
= 
=  =
=  = 0
= 0
 x = 0
x = 0
Krümmungstabelle von f2 :
| x < | –1 | < x < | 0 | < x < | 1 | < x | |
|---|---|---|---|---|---|---|---|
| Zähler von f2'' | – | – | – | 0 | + | + | + |
| Nenner von f2'' | + | 0 | – | – | – | 0 | + |
| f2''(x) | – | # | + | 0 | – | # | + |
| f2'(x) | fällt | # | steigt | Max. | fällt | # | steigt |
| Graf von f2 | Rechts- kurve | # | Links- kurve | WEP(0 | 0) | Rechts- kurve | # | Links- kurve |
Krümmungsverhalten von f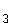 (x) =
(x) = 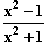 :
:
f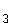 '(x) =
'(x) = 
 f
f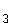 ''(x) =
''(x) = 
 =
=  = 0
= 0
 3x
3x = 1
= 1 


 = ±
= ±
Krümmungstabelle von f3 :
| x < | – | < x < |  | < x | |
|---|---|---|---|---|---|
| Zähler von f3'' | – | 0 | + | 0 | – |
| Nenner von f3'' | + | + | + | + | + |
| f3''(x) | – | 0 | + | 0 | – |
| f3'(x) | fällt | Min. | steigt | Max. | fällt |
| Graf von f3 | Rechts- kurve | WEP(– |–0,5) |–0,5) | Links- kurve | WEP( |–0,5) |–0,5) | Rechts- kurve |
Krümmungsverhalten von f (x) =
(x) = 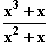 :
:
 '(x) =
'(x) =  , x ≠ 0
, x ≠ 0
 f
f ''(x) =
''(x) = 
= 
 =
= 
f4''(x) = 0  keine Lösung
keine Lösung
Krümmungstabelle von f4 :
| x < | –1 | < x ≠ 0 | |
|---|---|---|---|
| Zähler von f4'' | + | + | + |
| Nenner von f4'' | – | 0 | + |
| f4''(x) | – | # | + |
| f4'(x) | fällt | # | steigt |
| Graf von f4 | Rechts- kurve | # | Links- kurve |
30.
 ; c
; c 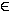 IR
IR  n
n 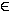
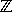 \{–1}
\{–1}
31.
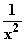 =
= 

 =
=  , c
, c 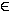 IR.
IR.
b) f(x) = 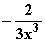 =
= 


 =
=  , c
, c 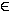 IR.
IR.
c) f(x) = 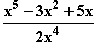 =
= 

 =
= 
=  , c
, c 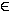 IR
IR
( =  + c, c
+ c, c 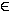 IR.)
IR.)
32.1
32.2
32.3
 ∞
∞ 
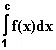 =
= 
 1
1
Der Grenzwert 1 ist die Maßzahl der nach rechts unbegrenzten „trichterförmigen“ Fläche zwischen der
Grafische Veranschaulichung:






 , w. z. b. w.
, w. z. b. w. =
=  =
= 

 =
=