Lösungen zu

6. Berechnung von Schnittpunkten:

Aufgabe 6.1

Der Schnittpunkt mit der y-Achse ist T(0/t).
Schnittpunkt mit x-Achse: y=0 setzen und x-Wert berechnen - der Punkt ist dann N(xo/0).

  1. T(0/3,5)
    , also N(1,75/0)
  2. T(0/-7)
    , also N(1,4/0)
  3. T(0/2)
    , also N(/0)
  4. T(0/2,5)
    , also N(6,25/0)
  5. T(0/)
    , also N(/0)
  6. T(0/
    , also N(/0)

 

Aufgabe 6.2

a)

Funktionsterme gleichsetzen:

||
|

dies ist der x-Wert des Schnittpunktes, diesen in eine der Gleichungen einsetzen:

also

Schnittpunkt: S(2/10)

b)

| |
|

x-Wert in eine der Gleichungen einsetzen

also

Schnittpunkt: S(8/45)

c)

| |
|
,

x-Wert in eine der Gleichungen einsetzen

also

Schnittpunkt: S(/5)

d)

Die Geraden haben gleiche Steigung m=7, sind also parallel.

Setzt man die Funktionsterme gleich, so erhält man eine falsche Aussage, also keinen Schnittpunkt.

7x - 14 = 7x -3 |-7x
-14 = -3 f.A.

e)

| |
 |

x-Wert in eine der Gleichungen einsetzen

also

Schnittpunkt: S(36/2)

f)

wegen Gerade 2:

Schnittpunkt S(-2/0,5)

 

Aufgabe 6.3

Man berechnet zuerst den Schnittpunkt zweier Geraden und setzt diesen dann in die dritte Gerade ein. Wenn er auch auf dieser liegt, ist die Aufgabe erfüllt.

z.B. Funktionsterme von g2 und g3 gleichsetzen:

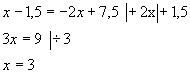
, also ist der Schnittpunkt S(3/1,5)

Dieser wird nun in g1 eingesetzt:
, dies ist eine wahre Aussage, also ist S der gemeinsame Schnittpunkt aller drei Geraden.