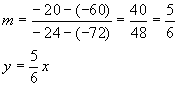Aufgabe 7.1

a) Die Koordinaten des Punktes P in einsetzen:
, also erhält man die Geradengleichung

b) P in
also

c) P in
also

d) P in
also

Aufgabe 7.2

a) parallel zur x-Achse, d.h. m = 0
durch P(-3/4), d.h. t = 4, also y = 4

b) parallel zur Winkelhalbierenden des 2. Quadranten bedeutet m = -1
also Q(2/5) in einsetzen:

c) parallel zur y-Achse, d.h. keine Funktionsgleichung sondern Relation
durch R(-4/2) bedeutet x = -4

d) parallel zur Winkelhalbierenden des 1. Quadranten bedeutet m = 1
also S(2/-3) in einsetzen:

e) durch den Ursprung, d.h. t = 0
parallel zur Geraden AB, also gleiche Steigung: