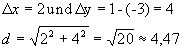
Lösungen zu
9. Abstände und Flächen:
Aufgabe 9.1

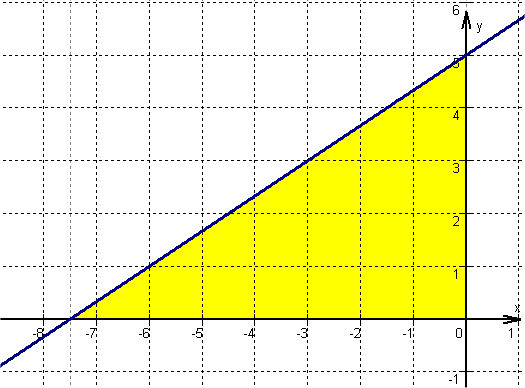
Die Formel für die Fläche
eines Dreiecks lautet ![]() , wobei g für Grundlinie und h für Höhe steht. Da das Dreieck
rechtwinklig ist, können die Seiten auf den Achsen als Grundlinie und Höhe
genommen werden.
, wobei g für Grundlinie und h für Höhe steht. Da das Dreieck
rechtwinklig ist, können die Seiten auf den Achsen als Grundlinie und Höhe
genommen werden.
Die Höhe beträgt 5 LE (t = 5), für die Angabe der Grundlinie
muss der Schnittpunkt mit der x-Achse berechnet werden:
![]() , die Grundlinie beträgt 7,5 LE.
, die Grundlinie beträgt 7,5 LE.
Also erhält man ![]() FE.
FE.
Aufgabe 9.2
a) 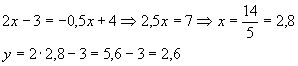
der Schnittpunkt ist also S(2,8/2,6)
b) 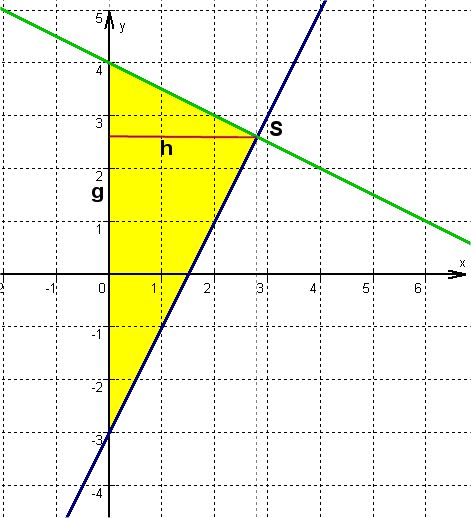
Nimmt man die Seite auf der y-Achse
als Grundlinie (g = 7), so ist der x-Wert des Schnittpunktes S die Länge
der Höhe des Dreiecks: h = 2,8 .
Als Fläche erhält man ![]() .
.
Aufgabe 9.3
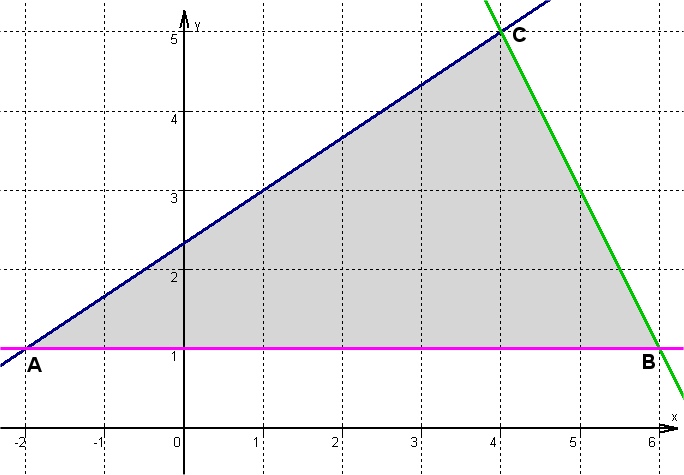
a) Gerade AB: die Gerade verläuft
waagrecht, hat also Steigung m = 0, der y-Wert der Punkte A und B ist 1, die
Gleichung lautet demnach y = 1 . (Auch rechnerisch erhält man Steigung
![]() .)
.)
Gerade AC: 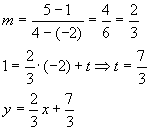
Gerade BC: 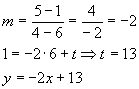
b) Seitenlänge der Seite AB:
![]()
Seite AC: 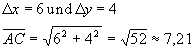
Seite BC: 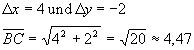
c) Die Grundlinie hat die Länge
g = ![]() . Der Abstand des Punktes C von der Grundlinie ist h = 5 - 1 = 4.
. Der Abstand des Punktes C von der Grundlinie ist h = 5 - 1 = 4.
Die Fläche ist ![]() .
.
Aufgabe 9.4
a) 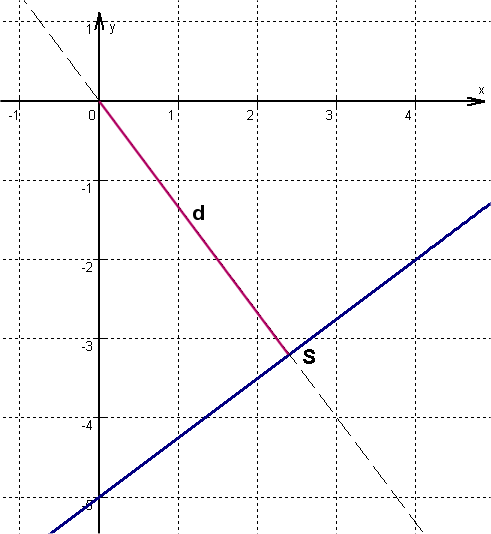
Zuerst wird der Schnittpunkt der Senkrechten durch den Ursprung mit der gegebenen Geraden berechnet, dann der Abstand des Punktes S vom Ursprung.
Steigung der Senkrechten: ![]() (Ursprungsgerade!)
(Ursprungsgerade!)
Schnittpunkt S:
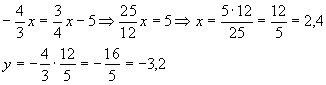
also ist der Schnittpunkt S(2,4/-3,2)
Abstand d:
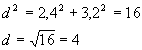
b) Senkrechte durch Ursprung: y =
2x
Schnittpunkt:
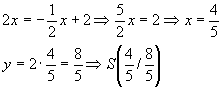
Abstand:
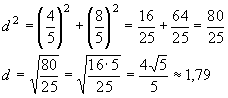
Aufgabe 9.5
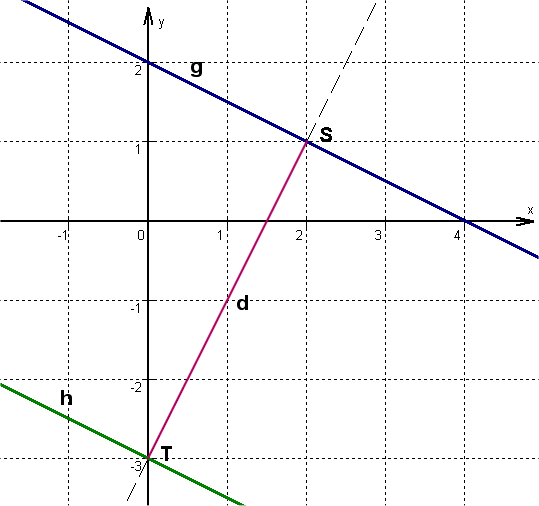
Zuerst stellt man die Gleichung der Senkrechten durch den Punkt T(0/-3) der Geraden h auf (alternativ geht auch der Punkt T(0/2) der Geraden g). Diese schneidet die Gerade g im Punkt S. Die Strecke TS ist der gesuchte Abstand.
Senkrechte durch T(0/-3): y = 2x
- 3
Schnittpunkt S:
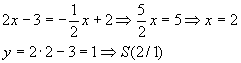
Abstand d: