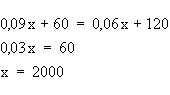Übungsblatt zur linearen Funktion:
Lösungen zu den Aufgaben 10 - 16
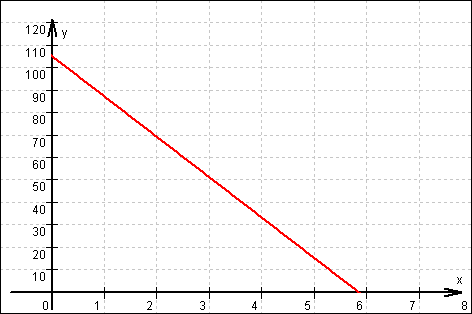
10. (a) Graf:
 (b) Zuordnung Zeit x
(b) Zuordnung Zeit x 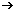 Wassermenge f(x): f(x) = 105 – 18 x
(c) f(x) = 0
Wassermenge f(x): f(x) = 105 – 18 x
(c) f(x) = 0  105 – 18 x = 0
18 x = 105
105 – 18 x = 0
18 x = 105
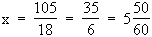 Die Wanne ist nach 5 Minuten und 50 Sekunden leer.
11. (a) Graf:
Die Wanne ist nach 5 Minuten und 50 Sekunden leer.
11. (a) Graf:
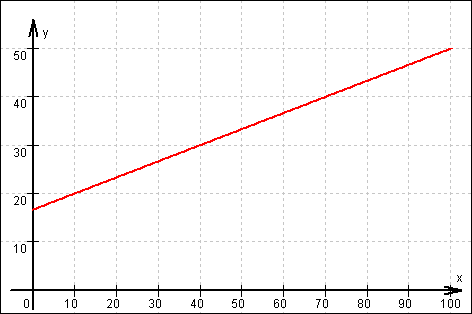 (b) Anfängliche Wassermenge in der Tonne:
(b) Anfängliche Wassermenge in der Tonne: 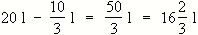 (c) Zuordnung Zeit x
(c) Zuordnung Zeit x 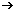 Wassermenge f(x):
Wassermenge f(x): 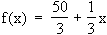 (d) f(x) = 50
(d) f(x) = 50 
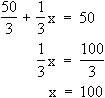 Der Regenschauer müsste 100 Minuten dauern.
12. (a) Graf:
Der Regenschauer müsste 100 Minuten dauern.
12. (a) Graf:
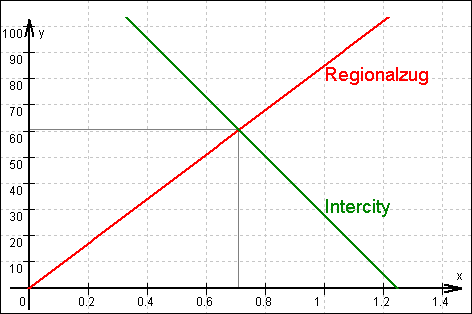 Die Züge begegnen sich etwa nach 0,7 Stunden, also um 9.42 Uhr,
und zwar etwa 61 km vom Bahnhof A entfernt.
(b) Zuordnung Zeit x
Die Züge begegnen sich etwa nach 0,7 Stunden, also um 9.42 Uhr,
und zwar etwa 61 km vom Bahnhof A entfernt.
(b) Zuordnung Zeit x 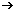 Entfernung f(x) von A:
Regionalzug: fre(x) = 85 x ;
Intercity: fic(x) = -113 x + t
Bestimmung von t:
Entfernung f(x) von A:
Regionalzug: fre(x) = 85 x ;
Intercity: fic(x) = -113 x + t
Bestimmung von t:
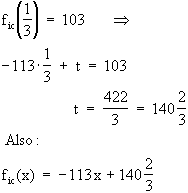 13. (a)
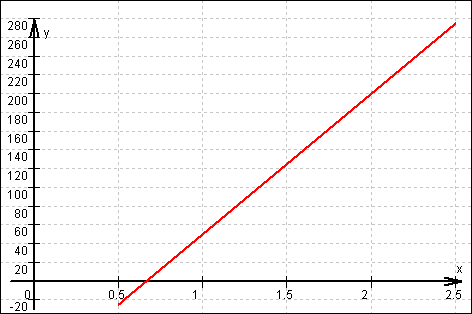
13. (a) 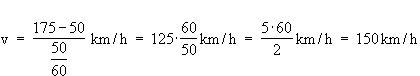 Graf:
Graf:
 (b) Zuordnung Zeit x
(b) Zuordnung Zeit x  gefahrene Autobahnstrecke f(x):
f(x) = 150 x + t
Bestimmung von t:
f(1) = 50
gefahrene Autobahnstrecke f(x):
f(x) = 150 x + t
Bestimmung von t:
f(1) = 50  150 + t = 50
150 + t = 50  t = -100
Also: f(x) = 150 x – 100
Wo befindet sich der Sportwagen um 1.15 Uhr?
f(1,25) = 150 · 1,25 – 100 = 87,5
(c) f(x) = 0
t = -100
Also: f(x) = 150 x – 100
Wo befindet sich der Sportwagen um 1.15 Uhr?
f(1,25) = 150 · 1,25 – 100 = 87,5
(c) f(x) = 0 
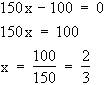 Der Sportwagen fuhr also um 0.40 Uhr auf die Autobahn.
f(x) = 210
Der Sportwagen fuhr also um 0.40 Uhr auf die Autobahn.
f(x) = 210 
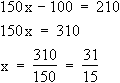 Der Sportwagen passiert den dritten Kontrollpunkt um 2.04 Uhr.
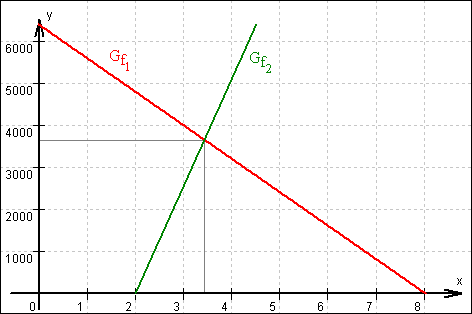
14. (a) f1(x) = –800 x + 6400 ;
f2(x) = 2560 x + t
f2(2) = 0
Der Sportwagen passiert den dritten Kontrollpunkt um 2.04 Uhr.
14. (a) f1(x) = –800 x + 6400 ;
f2(x) = 2560 x + t
f2(2) = 0  5120 + t = 0
5120 + t = 0  t = –5120
t = –5120  f2(x) = 2560 x – 5120
Graf:
f2(x) = 2560 x – 5120
Graf:
 (b) f1(x) und f2(x) gleichsetzen:
(b) f1(x) und f2(x) gleichsetzen:
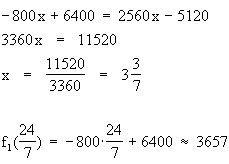 Sie treffen sich also um 3.26 Uhr, und zwar 3657 km von Frankfurt entfernt.
15. (a) f1(x) = 120 x ;
f2(x) = 160 x + t
f2(0,25) = –20
Sie treffen sich also um 3.26 Uhr, und zwar 3657 km von Frankfurt entfernt.
15. (a) f1(x) = 120 x ;
f2(x) = 160 x + t
f2(0,25) = –20  40 + t = –20
40 + t = –20  t = –60
t = –60  f2(x) = 160 x – 60
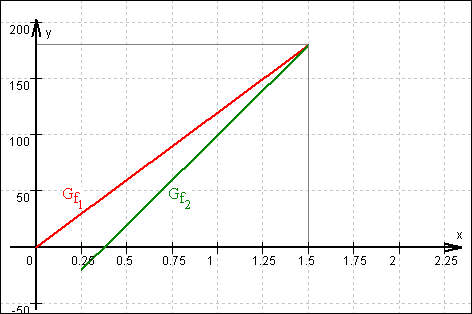
Graf:
f2(x) = 160 x – 60
Graf:
 (b) f1(x) und f2(x) gleichsetzen:
(b) f1(x) und f2(x) gleichsetzen:
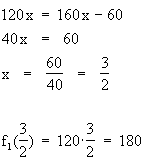 Die Polizei holt den Täter also um 15.45 Uhr ein,
und zwar 180 km nach dem Autobahnbeginn.
16. (a) h1(x) = 0,09 x + 60 ; h2(x) = 0,06 x + 120
(b) Graf:
Die Polizei holt den Täter also um 15.45 Uhr ein,
und zwar 180 km nach dem Autobahnbeginn.
16. (a) h1(x) = 0,09 x + 60 ; h2(x) = 0,06 x + 120
(b) Graf:
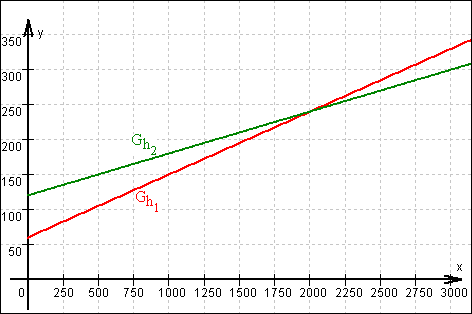 (c) Aus der Grafik ergibt sich schon, dass der Tarif H2
ab 2000 jährlich verbrauchten kWh günstiger ist.
Rechnerische Bestätigung:
(c) Aus der Grafik ergibt sich schon, dass der Tarif H2
ab 2000 jährlich verbrauchten kWh günstiger ist.
Rechnerische Bestätigung:
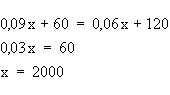
 (b) Zuordnung Zeit x
(b) Zuordnung Zeit x 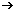 Wassermenge f(x): f(x) = 105 – 18 x
(c) f(x) = 0
Wassermenge f(x): f(x) = 105 – 18 x
(c) f(x) = 0  105 – 18 x = 0
18 x = 105
105 – 18 x = 0
18 x = 105
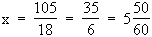 Die Wanne ist nach 5 Minuten und 50 Sekunden leer.
11. (a) Graf:
Die Wanne ist nach 5 Minuten und 50 Sekunden leer.
11. (a) Graf:
 (b) Anfängliche Wassermenge in der Tonne:
(b) Anfängliche Wassermenge in der Tonne: 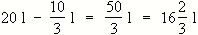 (c) Zuordnung Zeit x
(c) Zuordnung Zeit x 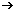 Wassermenge f(x):
Wassermenge f(x): 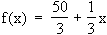 (d) f(x) = 50
(d) f(x) = 50 
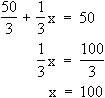 Der Regenschauer müsste 100 Minuten dauern.
12. (a) Graf:
Der Regenschauer müsste 100 Minuten dauern.
12. (a) Graf:
 Die Züge begegnen sich etwa nach 0,7 Stunden, also um 9.42 Uhr,
und zwar etwa 61 km vom Bahnhof A entfernt.
(b) Zuordnung Zeit x
Die Züge begegnen sich etwa nach 0,7 Stunden, also um 9.42 Uhr,
und zwar etwa 61 km vom Bahnhof A entfernt.
(b) Zuordnung Zeit x 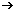 Entfernung f(x) von A:
Regionalzug: fre(x) = 85 x ;
Intercity: fic(x) = -113 x + t
Bestimmung von t:
Entfernung f(x) von A:
Regionalzug: fre(x) = 85 x ;
Intercity: fic(x) = -113 x + t
Bestimmung von t:
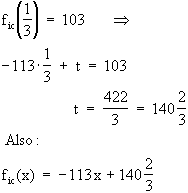 13. (a)
13. (a)  Graf:
Graf:
 (b) Zuordnung Zeit x
(b) Zuordnung Zeit x 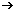 gefahrene Autobahnstrecke f(x):
f(x) = 150 x + t
Bestimmung von t:
f(1) = 50
gefahrene Autobahnstrecke f(x):
f(x) = 150 x + t
Bestimmung von t:
f(1) = 50  150 + t = 50
150 + t = 50  t = -100
Also: f(x) = 150 x – 100
Wo befindet sich der Sportwagen um 1.15 Uhr?
f(1,25) = 150 · 1,25 – 100 = 87,5
(c) f(x) = 0
t = -100
Also: f(x) = 150 x – 100
Wo befindet sich der Sportwagen um 1.15 Uhr?
f(1,25) = 150 · 1,25 – 100 = 87,5
(c) f(x) = 0 
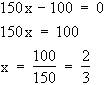 Der Sportwagen fuhr also um 0.40 Uhr auf die Autobahn.
f(x) = 210
Der Sportwagen fuhr also um 0.40 Uhr auf die Autobahn.
f(x) = 210 
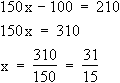 Der Sportwagen passiert den dritten Kontrollpunkt um 2.04 Uhr.
14. (a) f1(x) = –800 x + 6400 ;
f2(x) = 2560 x + t
f2(2) = 0
Der Sportwagen passiert den dritten Kontrollpunkt um 2.04 Uhr.
14. (a) f1(x) = –800 x + 6400 ;
f2(x) = 2560 x + t
f2(2) = 0  5120 + t = 0
5120 + t = 0  t = –5120
t = –5120  f2(x) = 2560 x – 5120
Graf:
f2(x) = 2560 x – 5120
Graf:
 (b) f1(x) und f2(x) gleichsetzen:
(b) f1(x) und f2(x) gleichsetzen:
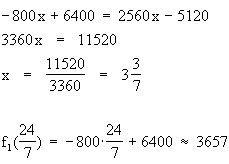 Sie treffen sich also um 3.26 Uhr, und zwar 3657 km von Frankfurt entfernt.
15. (a) f1(x) = 120 x ;
f2(x) = 160 x + t
f2(0,25) = –20
Sie treffen sich also um 3.26 Uhr, und zwar 3657 km von Frankfurt entfernt.
15. (a) f1(x) = 120 x ;
f2(x) = 160 x + t
f2(0,25) = –20  40 + t = –20
40 + t = –20  t = –60
t = –60  f2(x) = 160 x – 60
Graf:
f2(x) = 160 x – 60
Graf:
 (b) f1(x) und f2(x) gleichsetzen:
(b) f1(x) und f2(x) gleichsetzen:
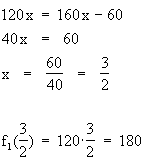 Die Polizei holt den Täter also um 15.45 Uhr ein,
und zwar 180 km nach dem Autobahnbeginn.
16. (a) h1(x) = 0,09 x + 60 ; h2(x) = 0,06 x + 120
(b) Graf:
Die Polizei holt den Täter also um 15.45 Uhr ein,
und zwar 180 km nach dem Autobahnbeginn.
16. (a) h1(x) = 0,09 x + 60 ; h2(x) = 0,06 x + 120
(b) Graf:
 (c) Aus der Grafik ergibt sich schon, dass der Tarif H2
ab 2000 jährlich verbrauchten kWh günstiger ist.
Rechnerische Bestätigung:
(c) Aus der Grafik ergibt sich schon, dass der Tarif H2
ab 2000 jährlich verbrauchten kWh günstiger ist.
Rechnerische Bestätigung: