Beispiele

Diese Seite dient dazu, einige Beispiele für Konstruktionen dokumentarisch zu beschreiben. Für weitere Beispiele sehen Sie bitte die Seiten mit den Demonstrationen an. Diese Seite ist zum Ausdrucken und Nachvollziehen gedacht.

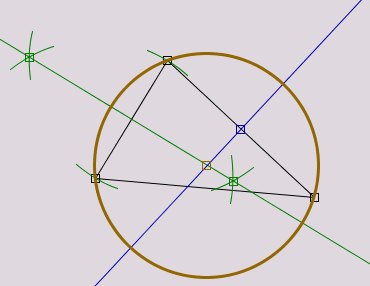
Umkreismittelpunkt

Wir beginnen mit einer einfachen Konstruktion.

• Als Ausgangspunkt wählen Sie das Streckenwerkzeug und erzeugen ein Dreieck. Wie Sie merken werden, braucht man das Punktwerkzeug dazu nicht.
• Nun wählen wir die grüne Farbe als Defaultfarbe durch Umstellen des Werkzeugs für die Farbwahl .
• Konstruieren wir nun die Mittelsenkrechte auf einer Seite. Dazu schlagen wir Kreise um die beiden Endpunkte durch den jeweils anderen Endpunkt.
• Da wir beide Schnittpunkte benötigen, nehmen wir das Schnittwerkzeug und klicken auf beide Kreisschnitte. Falls nicht beide sichtbar sind, so kann man entweder mit der Taste - herauszoomen, oder das Ausgangsdreieck durch Verschieben der Ecken (mit der rechten Maustaste) kleiner machen. Alternativ kann man nacheinander auf die beiden Kreise klicken.
• Mit dem Geradenwerkzeug verbinden wir die beiden Schnittpunkte.
• Wählen wir nun die blaue Farbe als Defaultfarbe.
• Die Mittelsenkrechte auf einer anderen Seite erzeugen wir durch eine Mogelkonstruktion. Wählen Sie das Mittenwerkzeug und klicken Sie die beiden Endpunkte an. Es entsteht der Punkt in der Seitenmitte.
• Wählen Sie das Senkrechten-Werkzeug und erzeugen Sie die Senkrechte zur Seite durch den Punkt.
• Nun wählen Sie die braune Farbe und das Kreiswerkzeug .
• Klicken Sie für den Mittelpunkt direkt in den Schnittpunkt der beiden Mittelsenkrechten. Sie werden gefragt, ob dieser Schnittpunkt erzeugt werden soll. Antworten Sie mit "Ja". Dies ist eine Abkürzung, bei der das Schnittwerkzeug nicht benötigt wird.
• Für den Radiuspunkt klicken Sie auf irgendeinen der Dreieckspunkte.
• Zur Dekoration rufen Sie jetzt den Eigenschaftsdialog der beiden grünen Kreise auf, indem Sie mit der rechten Maustaste auf die Kreise klicken. Stellen Sie die Kreise auf partiell sichtbar, indem Sie das Icon in der letzten Reihe aktivieren.
• Nun machen Sie noch den Umkreis fett , indem Sie im Eigenschaftsdialog des Umkreises wählen.

Fasskreis

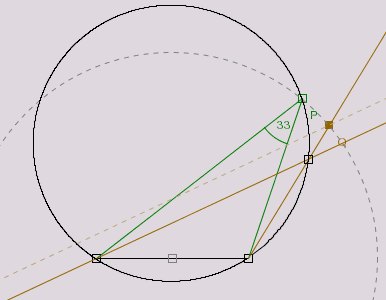
Es ist eines der hübschen geometrischen Tatsachen, dass der Winkel unter dem ein Kreissegment vom Kreis aus erscheint, konstant ist. Wir wollen dies auf zwei Arten demonstrieren. Zuerst konstruieren wir einen Kreis mit Segment und verschiebbarem Punkt und zeichnen die Größe des Winkels ein. Dann erzeugen wir den Fasskreis als Ortslinie.

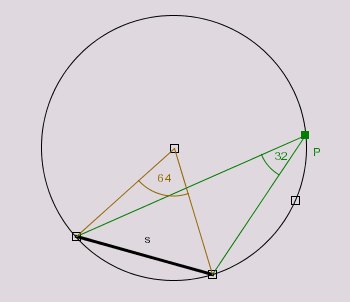
• Wählen Sie das Kreiswerkzeug und erzeugen Sie einen Kreis aus Mittelpunkt und Radiuspunkt.
• Wählen Sie das Werkzeug "Punkt auf Objekt" und erzeugen Sie die Endpunkte der Strecke. Bewegen Sie die Punkte. Sie bleiben immer auf dem Kreis.
• Nun erzeugen Sie die Strecke mit dem Streckenwerkzeug .
• Klicken Sie die Strecke mit der rechten Maustaste an, und machen Sie sie fett () und aktivieren Sie die Anzeige des Namens (), den Sie vorher auf "s" setzen.
• Nun wählen Sie die grüne Farbe, stellen Sie die Namensanzeige für neue Objekte an ( in der Werkzeugleiste) und die fette Darstellung ( in der Werkzeugleiste).
• Erzeugen Sie den Punkt P mit Hilfe des Werkzeugs "Punkt auf Objekt" . Er sollte mit den Default - Einstellungen fett und grün erscheinen. Natürlich können Sie die Einstellungen auch nachträglich an P vornehmen. Um den Namen auf P festzulegen, müssen Sie ohnehin den Eigenschaftendialog des Punktes aufrufen.
• Stellen Sie die fetten Objekte und die Namensanzeige wieder aus.
• Erzeugen Sie die Verbindungen von P zu den Endpunkten der Strecke.
• Erzeugen Sie den Winkel in P. Dazu stellen Sie die automatische Wertanzeige an ( in der Werkzeugleiste) und wählen das Winkelwerkzeug . Nun klicken Sie zuerst auf den linken Endpunkt der Strecke, dann auf P, dann auf den rechten Endpunkt der Strecke. Stellen Sie die automatische Wertanzeige wieder ab.
• Wählen Sie die braune Farbe und wiederholen Sie den letzten Schritt, um den Winkel im Mittelpunkt anzuzeigen.
• Die Anzeige des Mittelpunktswinkels ist nicht immer genau das Doppelte von der Anzeige des Fasskreiswinkels. Dies liegt an der Rundung der Anzeige. Zur Abhilfe könnten Sie die Nachkommastellen für Winkel im Menü heraufsetzen. Zur Demonstration wählen Sie einfach einen geraden Winkel.
• Bewegen Sie nun P, um sich von der Korrektheit der Konstruktion zu überzeugen.

Nun erzeugen wir den Fasskreis als Ortslinie.

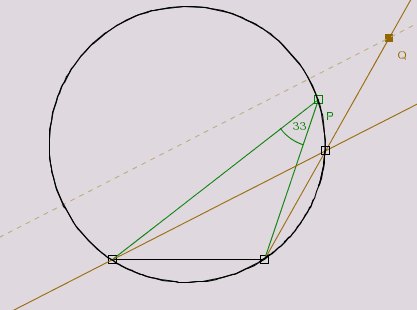
• Beginnen Sie mit der Konstruktion der Strecke in Schwarz ().
• Wählen Sie die Farbe grün, und setzen Sie den Punkt P (), die beiden Verbindungsstrecken () und den Winkel ().
• Mit Hilfe der Eigenschaftsdialoge schalten Sie die Namensanzeige des Punktes P, den Sie auf "P" setzen, ein (), und auch die Wertanzeige des Winkels bei P ().
• Wählen Sie die Farbe braun, und erzeugen Sie einen Strahl vom rechten Endpunkt der Strecke aus (). Klicken Sie dazu auf den Streckenpunkt und dann irgendwo in die freie Fläche rechts oben.
• Mit Hilfe des Eigenschaftsdialogs des Strahlpunktes, den Sie eben erzeugt haben, stellen Sie diesen Punkt auf fett () und nennen ihn "Q" ().
• Nun gilt es den Winkel in P an Q abzutragen. Dazu gibt es eine konstruktive Möglichkeit und eine berechnende Möglichkeit. Wir wählen hier die zweite, weil sie einfacher ist.
• Ermitteln Sie zunächst den Namen des Winkels, indem Sie mit der rechten Maustaste auf den Winkel klicken. Bei einer neuen Konstruktion sollte das "w1" oder "Winkel 1" sein.
• Wählen Sie nun das Winkelwerkzeug für Winkel mit fester Größe .
• Klicken Sie auf den rechten Endpunkt der Strecke, dann auf Q, und schließlich irgendwo in Richtung des gewünschten Winkels. Es öffnet sich ein Eigenschaftsdialog für den Winkel. Geben Sie als Wert -w1 ein. Falls der Name des Winkels ein Leerzeichen enthält, muss der Name in Anführungszeichen stehen, also etwa -"Winkel 1". Beachten Sie, dass der Winkel negativ abgetragen werden muss. Drücken Sie die Eingabetaste. Dies schließt den Dialog.
• Rufen Sie den Dialog für den abgetragenen Winkel nochmals auf, indem Sie auf den Schenkel mit der rechten Maustaste klicken. Machen Sie die Darstellung dünn ().
• Nun zeichnen Sie eine Parallele zu dem dünnen Schenkel durch den anderen Endpunkt der Strecke ().
• Erzeugen Sie den Schnittpunkt des Strahls mit der Parallelen ().
• Wählen Sie das Werkzeug für die Ortslinie . Wählen Sie den Schnittpunkt als Punkt für die Ortslinie aus.
• Bewegen Sie mit der linken Maustaste den Punkt Q einmal um die Strecke herum.

Man kann diese Ortslinie auch automatisch machen.

• Wählen Sie die dünne Darstellung in Schwarz.
• Konstruieren Sie den Mittelpunkt der Strecke ().
• Schlagen Sie einen Kreis um den Mittelpunkt durch P ().
• Wählen Sie das Werkzeug für die automatische Ortslinie .
• Als Punkt wählen Sie wieder den Schnittpunkt. Als Objekt wählen Sie den eben konstruierten dünnen Kreis. Als zu bewegenden Punkt nehmen Sie Q.

Schwerpunkt eines Vierecks

Für diese Konstruktion werden wir ein Makro verwenden. Der Trick ist, das Viereck in zwei Dreiecke aufzuteilen. Der Schwerpunkt liegt dann auf der Verbindungsgeraden der Schwerpunkte der beiden Dreiecke. Indem man das auf zwei verschiedene Arten macht, erhält man den Schwerpunkt als Schnittpunkt von zwei Geraden.

Dabei werden wir viermal das Makro "Schwerpunkt eines Dreiecks" anwenden.

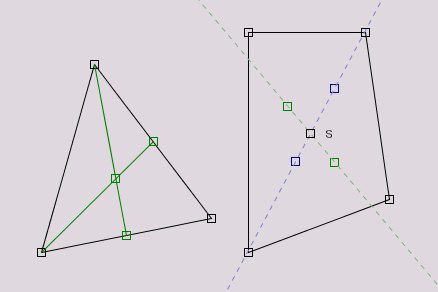
• Konstruieren Sie zunächst ein schwarzes Dreieck und daneben ein schwarzes Viereck ().
• In grün konstruieren Sie zwei Seitenmitten des Dreiecks () und verbinden diese mit den gegenüberliegenden Ecken ().
• Der Schnittpunkt der Verbindungen ist der Schwerpunkt des Dreiecks ().
• Nun müssen wir unser Makro erzeugen. Wählen Sie dazu das Werkzeug zum Erzeugen von Makros . Dieses Werkzeug nimmt dadurch die Gestalt an.
• Wählen Sie als Parameterobjekte die drei Ecken des Dreiecks. Sie müssen dazu im Auswahldialog jeweils den Punkt anwählen. Punkte sind schwarz gezeichnet.
• Klicken Sie erneut auf das Werkzeug , um die Zielobjekte auszuwählen. Das Werkzeug wird dadurch zu . Das Viereck verschwindet, weil es nicht aus den drei Parametern konstruierbar ist.
• Als Zielobjekt wählen Sie den Schwerpunkt des Dreiecks.
• Das Makro muss nun erzeugt werden. Dazu klicken Sie erneut auf . Es öffnet sich ein Dialog, in den Sie einen Namen für das Makro eintragen, z.B. "Schwerpunkt". Bestätigen Sie mit dem Knopf OK.
• Nun lassen wir das Makro viermal ablaufen.
• Zuerst wählen wir als Farbe grün und starten das Makro mit dem Werkzeug . Im Dialog wählen wir das einzig vorhandene Makro "Schwerpunkt" aus, z.B. durch Doppelklick.
• In der Statuszeile steht nun, dass ein Punkt verlangt wird. Wählen Sie also drei Punkte des Vierecks aus. Es müsste automatisch ein grüner Schwerpunkt erscheinen.
• Das Makro startet immer von neuem durch, wenn es einmal abgelaufen ist. Sie können also sofort den Schwerpunkt der anderen Hälfte des Vierecks berechnen.
• Verbinden Sie die beiden Schwerpunkte durch eine dünne grüne Gerade ().
• Schalten Sie auf blau, und erzeugen Sie auf die gleich Art und Weise die Schwerpunkte der beiden Dreiecke, die die andere Aufteilung des Vierecks ergeben, und eine dünne blaue Verbindungsgerade.
• Der Schnittpunkt () der beiden Geraden ist der Gesamtschwerpunkt.

Berechnete Konstruktionen

Als nächstes versuchen wir eine Konstruktion, die sich nur für gewisse Werte mit Zirkel und Lineal konstruieren lässt. Im Bild rollt der kleine grüne Kreis innen am großen schwarzen Kreis ab. Der Punkt A bewegt sich dabei längs der Ortslinie zum Punkt A*. Wenn K der Radius des großen und K-k der Radius des kleinen Kreises ist, so folgt

alpha*K = beta*(K-k),

weil ja die abgerollten Strecken gleich sein müssen. Dies ergibt eine Formel für beta, die sich allerdings nur dann konstruieren lässt, wenn K/(K-k) ganzzahlig ist. Wir verwenden daher arithmetische Ausdrücke, um beta zu definieren.

Beachten Sie dass die Ortslinie, die der Punkt A* beim Abrollen verursacht, nur für rationale Verhältnisse K/k periodisch ist, und nur für ganze Verhältnisse K/(K-k) einfach geschlossen. In der Abbildung wird dies nicht ganz genau realisiert (S ist frei verschiebbar).

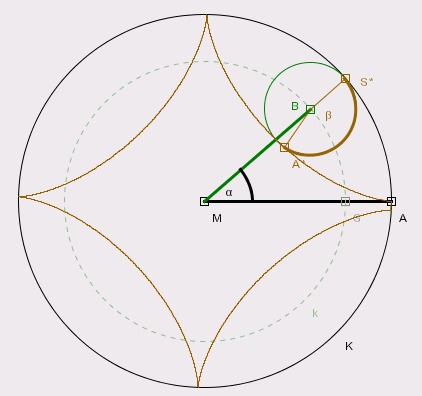
Die Konstruktion ist schon recht umfangreich, und es sind auch einige Details im obigen Bild versteckt.

• Zuerst wird der schwarze Kreis MA festgelegt, und K genannt.
• Auf der Strecke MA wählen wir einen Punkt (Punkt auf Objekt), den wir S nennen.
• Dies definiert den Kreis MS, den wir k nennen und dünn darstellen.
• Auf diesem Kreis legen wir B fest (Punkt auf Objekt), und dadurch die Strecke MB.
• Nun definieren wir den Winkel alpha als AMB (). Um den Winkel so zu nennen, geben wir "\a" als Namen ein.
• Aktivieren Sie für diesen Winkel die Option , damit der Winkel auch stumpf werden kann.
• Nun wird eine Gerade durch MB gelegt, die wir später verstecken.
• Diese Gerade wird mit dem Kreis K geschnitten.
• Den Schnittpunkt nennen wir S. Er wird dadurch automatisch zu S* umbenannt, weil S schon existiert.
• Wir zeichnen den grünen Kreis BS*.
• Jetzt kommt die Konstruktion (Berechnung) von Beta. Dazu aktivieren wir das Winkelwerkzeug und wählen S* und B. Bei der Wahl des dritten Punktes halten wir die Umschalttaste gedrückt und klicken irgendwo unten in das Bild. Es öffnet sich ein Dialog, wo man für den Winkel den Ausdruck -"\a"*K/(K-k) eingeben kann. Der Winkel "\a" muss in Anführungszeichen stehen, weil der Name ein Sonderzeichen enthält.
• Es entsteht ein Strahl durch B, den man mit dem Kreis schneidet. Dadurch entsteht der Schnittpunkt A*.
• Nun verstecken wir einige Zwischenschritte, insbesondere die Winkelgerade bei Beta, die wir durch eine Strecke BA* ersetzen.
• Schließlich kann man noch den Winkel Beta einzeichnen (als neuen Winkel A*BS*). Damit dieser Winkel den Kreis überdeckt, wählen wir eine große, dicke Darstellung (). Dadurch wird er immer in der Entfernung A*B von B gezeichnet.
• Nun wählen wir das Werkzeug für die automatische Ortslinie. Gezeichnet wird die Ortslinie von A*, wenn B auf k wandert.

Die Ortslinie ist nur dann ganz geschlossen, wenn S in spezieller Weise gewählt wird. Probieren Sie, S so zu fixieren, dass SA = MA/4 wird.

Eine angenäherte Winkeldreiteilung

Dieses Beispiel ist für mich nützlich, weil es mir die Gelegenheit gibt zu betonen, dass man einen beliebigen Winkel nicht mit Zirkel und Lineal dreiteilen kann. Selbstverständlich geht das aber mit berechneten Ausdrücken. Wir wollen aber hier eine Approximation gewinnen, die sehr einfach zu erklären ist, aber konstruktiv nicht das Einfachste, was man tun kann.

Unser erster Versuch ist einfach die Dreiteilung der Winkelsehne.

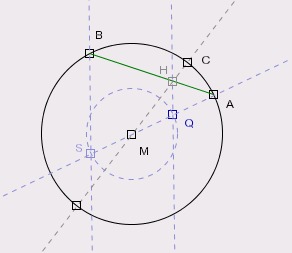
Dies ist eine sehr grobe Approximation.

• Erzeugen Sie den Kreis mit Mittelpunkt M und Radiuspunkt A.
• Setzen Sie B als Punkt auf dem Kreis ().
• Um die Sehne BA dreiteilen zu können, konstruieren wir die Mitte zwischen dem Kreismittelpunkt M und A ().
• Dann schlagen wir einen Kreis um M durch diesen Mittelpunkt und schneiden ihn mit der Geraden AM. Dies ergibt einen Schnittpunkt S.
• Nun erhalten wir den Drittelpunkt H der Sehne als Schnittpunkt der Parallelen zu BS durch Q und der Sehne AB.
• Als Approximation für die Winkeldreiteilung nehmen wir den Schnittpunkt C der Geraden MH mit dem Kreis.

Man kann nun sehen oder nachmessen, dass dieser Punkt nicht sehr gut dreiteilt, selbst dann wenn der Winkel AMB 90 Grad nicht übersteigt. Wir erzeugen nun ein Makro, dass diese grobe Dreiteilung durchführt.

• Dazu wählen wir das Werkzeug zum Erzeugen von Makros .
• Als Parameter für das Makro wählen wir den Kreis (und damit automatisch auch den Mittelpunkt M als sekundären Parameter), sowie die Punkte A und B.
• Nach erneutem Klick auf geben wir den Punkt C als Zielobjekt für das Makro ein.
• Als Name wählen wir "Grobe Dreiteilung".

Nun sollte man die Konstruktion abspeichern, und zwar mit dem Makro. Dazu muss die Option "Mit Makros Speichern" aktiv sein. Anschließend wählen wir "Neue Konstruktion". Das Makro bleibt dabei erhalten. Wir testen zunächst die Konstruktion.

• Erzeugen Sie den Kreis MA und den Objektpunkt B auf dem Kreis.
• Nun rufen Sie das Makro "Grobe Dreiteilung" auf ().
• Als Parameter ist der Kreis einzugeben und die Punkte A und B. Es sollte der Punkt C erscheinen. Hierbei erweist es sich als sinnvoll, die Eingabe-Prompts für das Makro, die bei der Definition des Makros im Dialog geändert werden können, aussagekräftig zu machen.
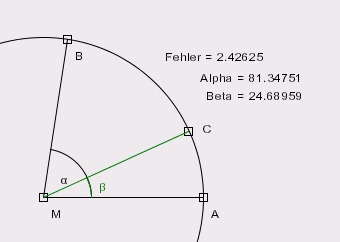
• Nun zeichnen wir die beiden Winkel AMB und AMC ein, die wir "\a" und "\b" nennen.
• Die Ausgaben rechts oben sind arithmetische Ausdrücke. Wählen Sie das Werkzeug , und klicken Sie an die entsprechenden Stellen, um die Ausdrücke zu erzeugen.
• Der oberste Ausdruck für den Fehler hat den Wert "\a"/3-"\b". Als Beschreibung wird "Fehler" eingegeben. Die Anzeige der Beschreibung muss dann noch aktiviert werden ().

Der Fehler (Alpha/3-Beta) wird umso kleiner, je kleiner Alpha wird. Im Viertelkreis wird er maximal 3.5 Grad. Bei 3.5 Grad ist er allerdings nur noch ein Tausendstel Grad. Dies bringt uns auf den Gedanken den Fehler einfach wieder zu dreiteilen und dadurch eine bessere Approximation zu erhalten.

Zur Verbesserung unserer Approximation verdreifachen wir Beta und dreiteilen Alpha-3*Beta grob. Diese Teilung addieren wir zu Beta.

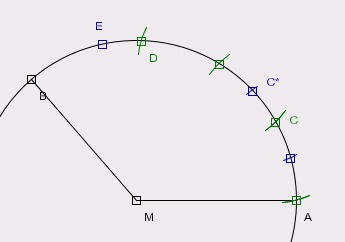
• Löschen wir zunächst die Winkel und die Strecken.
• Dann ziehen wir B nach links, damit ein großer Fehler entsteht.
• Nun schlagen wir einen Kreis um C durch A und erhalten damit den verdoppelten Winkel AMC. Dann noch einen Kreis um diesen neuen Punkt, und wir erhalten D. Der Winkel AMD ist das Dreifache von AMC.
• Nun rufen wir unser Makro "Grobe Dreiteilung" auf (), und teilen den Winkel DMB. Als Parameter sind der Kreis und die Punkte D, B anzugeben. Es entsteht der Punkt E.
• Den Bogen DE tragen wir nun von C aus ab. Dazu schlagen wir einen Kreis um C mit Radius DE mit dem Werkzeug für Kreise aus drei Punkten . Dadurch erhalten wir C*. Dies sollte eine bessere Approximation sein.
• Die Kreise machen wir nun noch partiell, um die Übersicht zu erhöhen.

Nun werden alle Details versteckt, und eine Testumgebung wie oben erzeugt. Der Fehler ist wie erwartet sehr klein.

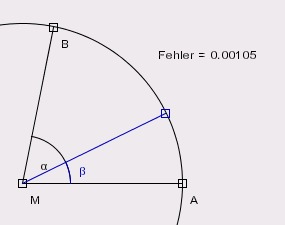
Damit die Approximation auf dem gesamten Kreis funktioniert, kann man den Winkel zunächst vierteln, dann approximativ dreiteilen, dann vervierfachen. Eine entsprechende Konstruktion finden Sie hier.