
Eine Pizzeria bietet zwei runde Pizzas mit derselben Dicke in verschiedenen Größen an. Die kleinere hat einen Durchmesser von 30 cm und kostet 30 Zeds. Die größere hat einen Durchmesser von 40 cm und kostet 40 Zeds.
Beispielaufgabe 1: Mathematische Grundbildung
Bei welcher Pizza bekommt man mehr für sein Geld? Gib eine Begründung an.
Du wirst beauftragt, einen neuen Satz von Münzen zu entwerfen. Alle Münzen sollen
rund und silberfarbig sein, aber verschiedene Durchmesser haben.
Forscher haben herausgefunden, dass ein idealer Satz von Münzen folgende
Anforderungen erfüllt:

Der Durchmesser der Münzen sollte nicht kleiner als 15 mm und nicht größer als 45 mm sein.
Beispielaufgabe 2: Mathematische Grundbildung
Entwirf einen Satz von Münzen, der die oben genannten Anforderungen erfüllt. Beginne mit einer 15-Millimeter-Münze. Dein Satz sollte so viele Münzen wie möglich enthalten.
Die weltweite Erwärmung hat zur Folge, dass das Eis einiger Gletscher schmilzt. Zwölf Jahre nach dem Wegschmelzen des Eises beginnen auf den Felsen winzige Pflanzen zu wachsen, die sogenannten Flechten.
Jede Flechte wächst ungefähr kreisförmig.
Der Zusammenhang zwischen dem Durchmesser dieses Kreises und dem Alter der Flechten kann mit folgender Formel angenähert bestimmt werden:
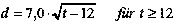
wobei d den Durchmesser der Flechte in Millimeter angibt und t die Zahl der Jahre, nach dem Wegschmelzen des Eises.
Beispielaufgabe 3: Mathematische Grundbildung
Berechne anhand der Formel den Durchmesser der Flechten 16 Jahre nach dem Wegschmelzen des Eises.
Gib deine Berechnung an.
Beispielaufgabe 4: Mathematische Grundbildung
Anne hat den Durchmesser einer Flechte gemessen und festgestellt, dass er
35 Millimeter beträgt.
Vor wie vielen Jahren ist das Eis an dieser Stelle verschwunden?
Gib deine Berechnung an.
Beispielaufgabe 5: Mathematische Grundbildung
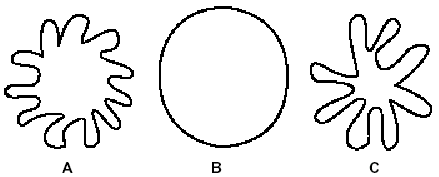
Welche der Figuren hat die größte Fläche? Begründe deine Antwort.
Beispielaufgabe 6: Mathematische Grundbildung
Gib eine Methode an, wie der Flächeninhalt von Figur C bestimmt werden kann.
Beispielaufgabe 7: Mathematische Grundbildung
Gib eine Methode an, wie der Umfang der Figur C bestimmt werden kann.
Die in etwa benötigte Strecke, um ein Fahrzeug zum Stillstand zu bringen, setzt sich zusammen aus:
Das unten abgebildete "Schneckendiagramm" gibt den theoretischen Anhalteweg für ein Fahrzeug unter guten Bremsbedingungen an (ein besonders aufmerksamer Fahrer, Bremsen und Reifen in tadellosem Zustand, trockene Straße mit einer guten Oberfläche) und zeigt, inwiefern der Anhalteweg von der Geschwindigkeit abhängt.
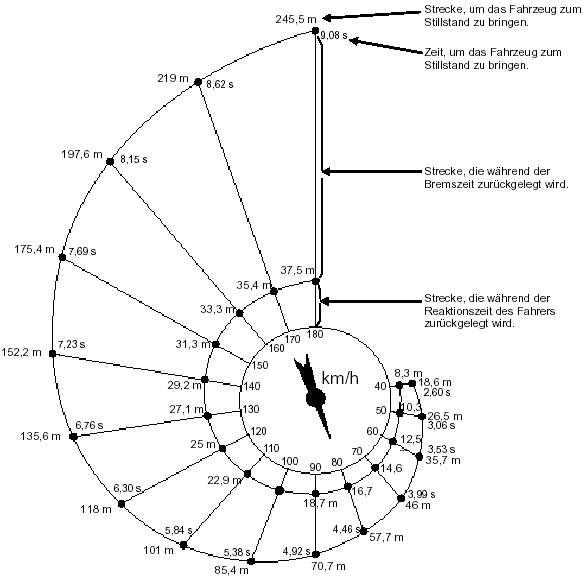
Beispielaufgabe 8: Mathematische Grundbildung
Ein Fahrzeug fährt mit einer Geschwindigkeit von 110 km/h. Welche Strecke legt es während der Reaktionszeit des Fahrers zurück?
Beispielaufgabe 9: Mathematische Grundbildung
Ein Fahrzeug fährt mit einer Geschwindigkeit von 110 km/h. Welche Strecke wird insgesamt zurückgelegt, bis das Fahrzeug zum Stillstand kommt?
Beispielaufgabe 10: Mathematische Grundbildung
Ein Fahrzeug fährt mit einer Geschwindigkeit von 110 km/h. Wie lange dauert es, um das Fahrzeug vollkommen zum Stillstand zu bringen?
Beispielaufgabe 11: Mathematische Grundbildung
Ein Fahrzeug fährt mit einer Geschwindigkeit von 110 km/h. Welche Strecke wird während der Betätigung der Bremsen zurückgelegt?
Beispielaufgabe 12: Mathematische Grundbildung
Eine zweite Fahrerin, die bei guten Fahrbedingungen unterwegs ist, bringt ihr Fahrzeug nach einer Gesamtstrecke von 70,7 Metern zum Stehen. Mit welcher Geschwindigkeit fuhr das Fahrzeug vor dem Betätigen der Bremsen?
Beispielaufgabe 13: Mathematische Grundbildung
Nick möchte die rechteckige Terrasse seines neuen Hauses pflastern. Die Terrasse ist 5,25 Meter lang und 3,00 Meter breit. Er benötigt 81 Pflastersteine pro Quadratmeter.
Berechne, wie viele Pflastersteine Nick für die ganze Terrasse braucht.
Eine Robbe muss atmen, auch wenn sie schläft. Martin hat eine Robbe eine Stunde lang beobachtet. Zu Beginn seiner Beobachtung befand sich die Robbe an der Wasseroberfläche und holte Atem. Anschließend tauchte sie zum Meeresboden und begann zu schlafen. Innerhalb von 8 Minuten trieb sie langsam zurück an die Oberfläche und holte Atem. Drei Minuten später war sie wieder auf dem Meeresboden, und der ganze Prozess fing von vorne an.
Beispielaufgabe 14: Mathematische Grundbildung
Nach einer Stunde war die Robbe: