|
|
f o r m i m e T e X Click for: mimeTeX quickstart full mimeTeX manual download mimeTeX |
|
|
|
f o r m i m e T e X Click for: mimeTeX quickstart full mimeTeX manual download mimeTeX |
|
| L a T e X P r a c t i c e B o x |
|
Enter any LaTeX math markup you like in the top box. Then press Submit to see it rendered. I've started you out with a little example already in the box. Or you can Click any example image in this tutorial to place its corresponding markup in the box. |
|
Now click "Submit" to see your expression
rendered below... |
LaTeX is a word processing program that lets you easily write documents containing complicated math. It's the math fragment of LaTeX's markup syntax that we'll briefly review here. Only the most basic features are discussed. And to keep the discussion short, examples sometimes illustrate features not explicitly explained in the text. Use the practice box above to try out anything you think I'm trying to tell you. The references below provide more complete information.
This tutorial accompanies mimeTeX, a LaTeX-like program that facilitates writing
math on the web. You write familiar html markup to format
your text, and you write <img> tags containing LaTeX
markup in query strings to format your math. For example,
<img src="http://www.bos-sozial.musin.de/cgi-bin/mimetex.cgi?\sqrt{a^2+b^2}">
displays
wherever you put that tag. To accommodate its web-centric focus,
mimeTeX has several syntax extensions not recognized by standard
LaTeX. Red text warns you when we're
discussing such mimeTeX extensions. Math markup containing them
won't be correctly processed by standard LaTeX.
Many ordinary keyboard characters are rendered just like you'd expect.
For example, typing
a...z,0...9,+-*/=()[] renders
.
But some characters have special LaTeX significance. For example,
underscore b_i introduces a subscript,
rendering
,
and carat a^n introduces a superscript,
rendering
.
These and some other special LaTeX characters are discussed
in more detail below.
In particular, the backslash character \ always
introduces special LaTeX symbols like
\alpha,\beta,\gamma...\omega (which renders
),
or introduces special Latex commands like
\frac 12 \sqrt \pi (which renders
).
When you want to see a displayed backslash, type either
\backslash or \setminus.
LaTeX special symbols and commands always begin with a backslash
\, almost always followed by one or more
alphabetic characters a-z,A-Z. The symbol or command
is always terminated by a space or by any non-alphabetic character.
For example, \frac2x can be typed without
a space between the \frac and the 2,
correctly rendering
.
And \frac\pi2 correctly renders
.
But \fracx2 is incorrectly interpreted as the
non-existent command \fracx followed by 2, so a space
is mandatory and you must type \frac x2
to render
.
There's one occasional exception to the preceding rules. A few LaTeX
symbols consist of a backslash followed by a single non-alphabetic
character. Among other keyboard characters, $,%,&
have special LaTeX significance, so to display them you have to type
\$,\%,\& instead, which renders
.
As illustrated above, \frac takes two arguments,
and \sqrt takes one. Similarly, subscripts
b_i and superscripts a^n
each take one argument. Some commands take no arguments. When needed,
each LaTeX argument is always the next single character following
the command. But any expression enclosed in curly braces is treated
as a single character, and the curly braces are not displayed.
For example, \frac1{\sqrt{a^2+b^2}} renders
.
Curly braces must always appear in properly balanced pairs.
Unnecessary pairs of curly braces usually do no harm, so use
them when in doubt. For example, \sqrt{\frac12}
renders
.
To display curly braces, type \lbrace...\rbrace
which renders
.
Besides our preceding examples, note that symbols may be
simultaneously subscripted and superscripted. For example,
A_{u,v}^k renders
.
Also note that sub/superscripts may themselves be
sub/superscripted to any level (though you may want
to reconsider your notation after two levels). For example,
A_{u_i,v_j}^{k_m^n} renders
.
Limits (lower and upper bounds) are written just like subscripts and superscripts. For example,
To make sure limits are displayed directly below and above the operator, begin your expression with \displaystyle. For example,
Enclosing terms in ordinary parentheses doesn't always look good. For example,
Instead, the LaTeX commands \left( ... \right) automatically size parentheses, and other delimiters, to match the enclosed term. For example,
Ordinary parentheses (...) don't have to be balanced, but \left(...\right) must always appear in properly balanced pairs. And any number of \middle| commands may appear between a \left(...\right) pair, to size contained delimiters similarly (see the third and fourth examples below). Besides \left(...\middle|...\right), the following delimiters can also be automatically sized:
| Delimiter | example... | ...renders |
| \left( ... \right) | \left( \frac1{1-x^2} \right)^2 |
|
| \left[ ... \right] | \left[ \frac1{\sqrt2}x-y \right]^2 |
|
| \left\{ ... \right\} | \left\{ x \in \mathbb{R} \middle| x \geq \frac12 \right\} |
|
| \left\langle ... ... \right\rangle |
\left\langle \varphi \middle| \hat{H} \middle| \phi \right\rangle |
|
| \left| ... \right| | \left| \begin{matrix} a_1 & a_2 \\
b_1 & b_2 \end{matrix} \right| |
|
| \left\| ... \right\| | \left\| x^2-y^2 \right\| |
|
| \left\{ ... \right. | y = \left\{ \text{this\\that} \right. |
|
| \left. ... \right\} | \left. \text{this\\that} \right\} = y |
|
Note the last two examples. Any left delimiter can be balanced with a matching \right. and any right delimiter can be balanced with a preceding \left. The . delimiter balances its mate but displays nothing, which lets you format math expressions like the last two illustrated above. The \text{ } and \\ commands from those examples are discussed below.
Use the LaTeX "math accent" \vec{ }
to write vectors. For example, \vec{v}
renders
,
and \widevec{ABC} renders
.
Each accent has a wide counterpart, used when its argument contains
more than a single character.
Among the accents LaTeX recognizes are the following:
| Accent | example... | ...renders |
| \vec{ } | \widevec{ABC} |
|
| \hat{ } | \widehat{ABC} |
|
| \tilde{ } | \widetilde{ABC} |
|
| \dot{ } | \dot{\omega} |
|
| \ddot{ } | \ddot{\omega} |
|
While not strictly accents, the following one-argument commands are also very useful. They have no wide counterparts: \not{ } accepts only a single-character argument, whereas \cancel{ }, \sout{ }, \overline{ } and \underline{ } all accept one or more characters.
| Command | example... | ...renders |
| \not{ } | a \not= b |
|
| a \not\in \mathbb{Q} |
| |
| \cancel{ } | \cancel{ABC} |
|
| \sout{ } | \sout{ABC} |
|
| \overline{ } | \overline{ABC} |
|
| \underline{ } | \underline{ABC} |
|
While also not accents, the following two-argument commands are similarly useful. Note that \overbrace{ }^{ } requires a carat ^ between its two arguments, whereas \overset{ }{ } doesn't. Similarly, \underbrace{ }_{ } requires an underscore _, whereas \underset{ }{ } doesn't.
| Command | example... | ...renders |
| \overbrace{ }^{ } | \overbrace{a,...,a}^{\text{k a's}} |
|
| \underbrace{ }_{ } | \underbrace{b,...,b}_{\text{l b's}} |
|
| \overset{ }{ } | a \overset{\text{def}}{=} b |
|
| \underset{ }{ } | c \underset{\text{def}}{=} d |
|
You can usefully combine
\overbrace{ }^{ } and
\underbrace{ }_{ } so that, for example,
\underbrace{\overbrace{a...a}^{\text{k a's}},
\overbrace{b...b}^{\text{l b's}}}_{\text{k+l elements}}
renders
.
Writing sin^2\theta+cos^2\theta renders
,
whereas \sin^2\theta+\cos^2\theta renders
.
Several dozen common function names are recognized by LaTeX as
backslashed commands, and rendered in a roman font that's more
typical mathematical notation. And some of these function name
commands like \lim render subscripts more
typically, too. For example, \lim_{x\to\infty}\frac1x=0
renders
.
The most common LaTeX function name commands are listed below.
Those that treat subscripts like \lim are
followed by an underscore, e.g., \lim_.
| \arccos | \arcsin | \arctan | \arg | \cos |
| \cosh | \cot | \coth | \csc | \deg |
| \det_ | \dim | \exp | \gcd_ | \hom |
| \inf_ | \ker | \lg | \lim_ | \liminf_ |
| \limsup_ | \ln | \log | \max_ | \min_ |
| \Pr_ | \sec | \sin | \sinh | \sup_ |
| \tan | \tanh |
The easiest way to write a matrix in LaTeX is
\begin{matrix} a&b\\c&d \end{matrix}
which renders
.
Surround it with \left( ... \right)
to obtain
.
Alternatively, \begin{pmatrix} ... \end{pmatrix}
automatically surounds the rendered matrix with parentheses.
Matrices are written row-wise, with \\ at the end of each row. Within a row, columns are separated by &. A general m x n matrix is therefore written in the form
| \begin{matrix} | |||||||
| a1,1 | & | a1,2 | & | . . . | & | a1,n | \\ |
| a2,1 | & | a2,2 | & | . . . | & | a2,n | \\ |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | \\ |
| am,1 | & | am,2 | & | . . . | & | am,n | |
| \end{matrix} |
Each component ai,j can contain
any valid LaTeX markup whatsoever, even another matrix.
If you write & &,
the corresponding component is left blank. For example,
\begin{pmatrix} a&\\&b \end{pmatrix}
renders the diagonal 2 x 2 matrix
.
You can terminate a row with \\ anytime,
so the preceding a&\\&b can
been written a\\&b.
And you can write (lower left) triangular matrices without
strings of empty & & &'s.
LaTeX does its own spacing, and spaces that you type yourself
are never displayed. For example, (abcd),
(a bcd), (a b cd)
and (a b c d)
all render the same
.
To explicitly embed displayed space, LaTeX provides several commands
including
\, \: \; \quad \qquad,
and also a backslashed blank
(i.e., a \ followed by a blank).
These commands take no arguments. For example,
(a\,b\:c\;d\ e\quad f\qquad g)
renders
.
For arbitrary embedded space, mimeTeX provides the
command \hspace{ } which takes a single
numerical argument that specifies the width of the embedded space in
pixels. For example, \hspace9 embeds 9 pixels
and \hspace{25} embeds 25 pixels, so
(ab\hspace9cd\hspace{25}ef) renders
.
To begin a new line, mimeTeX provides the command
\\. For example,
x=1\\y=2\\z=3 renders
.
Typing abcdef renders
in LaTeX's default math font. To intersperse explanatory text,
\text{abc def} renders
in non-mathematical roman font. Note that embedded spaces in
\text{ } are respected. For example,
Standard LaTeX provides many font sizes. A few examples of commands that select font size are \tiny, \small, \normalsize (the usual default), \large, \Large, \LARGE, \huge and \Huge. These commands take no arguments. But they're not permitted within math markup by standard LaTeX.
MimeTeX permits the above eight font size commands within math markup. For example,
| \tiny\sqrt{a^2+b^2} | renders |
|
| \small\sqrt{a^2+b^2} |
| |
| \normalsize\sqrt{a^2+b^2} |
| |
| \large\sqrt{a^2+b^2} |
| |
| \Large\sqrt{a^2+b^2} |
| |
| \LARGE\sqrt{a^2+b^2} |
| |
| \huge\sqrt{a^2+b^2} |
| |
| \Huge\sqrt{a^2+b^2} |
|
A font size command applies to everything to its
right, unless a subsequent command changes the font size again.
For example,
\small abc\large def\LARGE ghi
renders
.
But the scope of a font size command is limited to the
{...}-enclosed subexpression in which it occurs.
For example, abc{\LARGE def}ghi
renders
.
MimeTeX default-renders expressions
\displaystyle
at sizes \large and larger,
and default-renders them
at sizes \normalsize and smaller.
To override the \large default,
begin your expression with \textstyle
Here are several examples further demonstrating LaTeX features and usage. Some of the illustrated features haven't been discussed in this tutorial, and you'll have to consult the references for an explanation. To see how the examples are done, Click any one of them to place its corresponding markup in the Practice Box above. Then press Submit to re-render it, or you can edit the markup first to suit your own purposes.
| (1) |
|
|||
| (2) |
|
|||
| (3) |
|
solution for quadratic | ||
| (4) |
|
definition of derivative | ||
| (5) |
|
continued fraction | ||
| (6) |
|
illustrating \left\{...\right. and note the accents |
||
| (7) |
|
\overbrace{}^{} and \underbrace{}_{} (TeXbook page 181, Exercise 18.41) |
||
| (8) |
|
illustrating \begin{array}...\end{array} | ||
| (9) |
|
using \begin{eqnarray} to align equations | ||
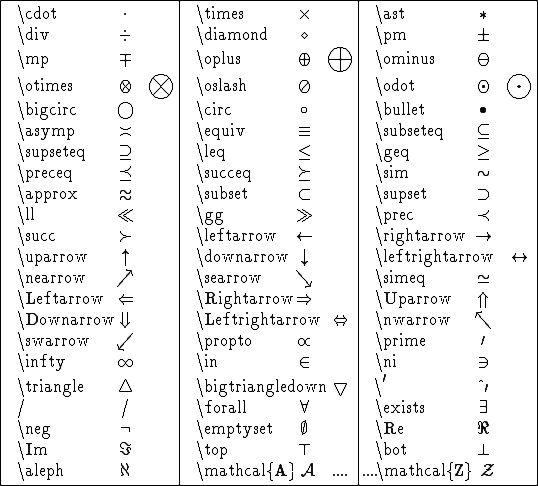
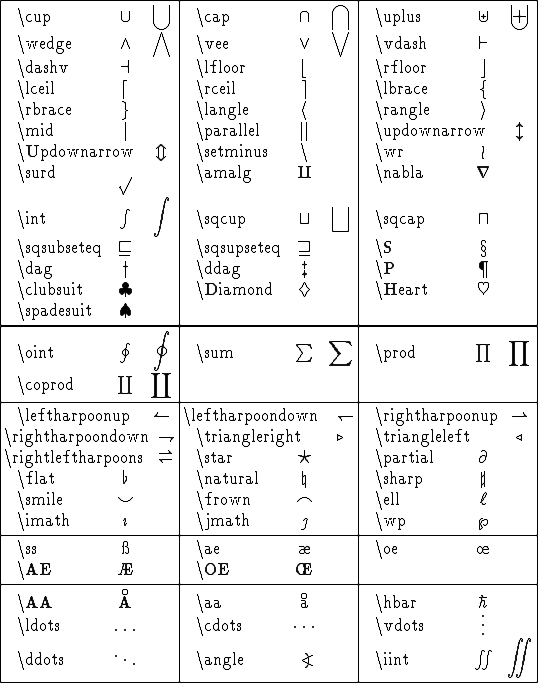
You've already seen several LaTeX symbols like \alpha, \beta and \omega, and several LaTeX commands like \frac, \sqrt and \sum. The Comprehensive LaTeX Symbol List illustrates over 2,500 symbols supported by LaTeX. Some of the basic symbols and commands are illustrated in the following tables.
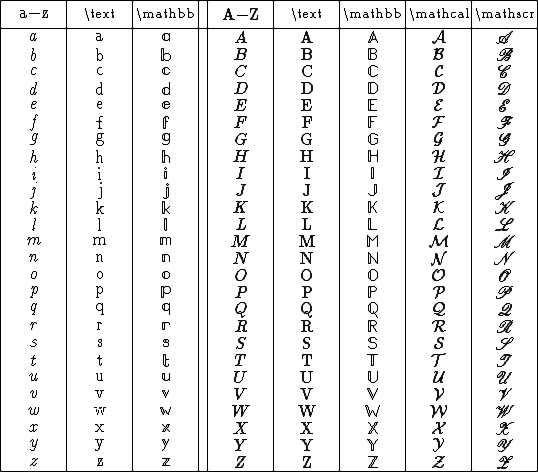
Simply typing a-z,A-Z renders characters
in LaTeX's default math font, while typing
\mathbf{a-z,A-Z} renders
in bold math font. And
typing \text{a-z,A-Z} renders characters
in roman font. Spaces inside \text{ }
are rendered exactly as typed, for example,
\text{this is a test} renders
.
LaTeX supports many useful fonts besides math and roman. Among these are
| Blackboard bold: | \mathbb{a-z,A-Z} | renders |
|
| Calligraphic: | \mathcal{A-Z} |
| |
| Script: | \mathscr{A-Z} |
|
The blackboard bold font contains many characters besides
a-z,A-Z. Calligraphic and script fonts contain
uppercase A-Z only. You'd typically type
only one character at a time in these fonts. For example,
x\in\mathbb{R}_+ renders
.
But, just like \text{ }, any number of
characters is permitted between the { }'s.
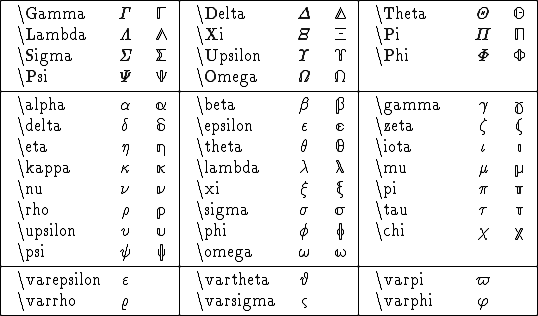
Characters from the Greek alphabet supported by LaTeX.
The \mathbb{ } versions are
also illustrated. For example, \mathbb{\lambda}
renders
.
The operators shown in two sizes below are automatically
"promoted" to the larger size in LaTeX's \displaystyle
mode. For example,
f(x)=\int_{-\infty}^x e^{-t^2}dt renders
, whereas
\displaystyle f(x)=\int_{-\infty}^x e^{-t^2}dt
renders
.
The arrangement of symbols in the tables will be improved in a future version of this tutorial.
This tutorial discusses LaTeX's mathematical markup capabilities, ignoring the preparation of documents containing formatted text. Most references explain LaTeX's mathematical markup, but emphasize the preparation of complete documents. The TeX Users Group provides lists of online resources and book resources that you may find useful.
Among the online resources, the two pages Latex Math I and Latex Math II comprise another short LaTeX math tutorial. And The not so Short Introduction to LaTeX is a good general online LaTeX reference.
If you're only interested in LaTeX for online mathematical markup (and not for document preparation), then you may not want to invest the time and money that books entail. But in case you do want a book, try to browse as many as you can, and then choose the one or two you personally like best. Among the book resources, here are a few you might want to look at:
Intermediate: A Guide to LaTeX2e, 4th ed. is authoritative and easy to read, with a good math discussion.
Advanced: at 1100 pages it's not a suitable tutorial or first book, but the most comprehensive LaTeX reference available is, The LaTeX Companion, 2nd ed., Frank Mittelbach and Michel Goossens, Addison-Wesley 2004, ISBN 0-201-36299-6 ($59.99).
Math: Math into LaTeX, 3rd ed., George Gratzer, Birkhauser Boston 2000, ISBN: 0-8176-4131-9 emphasizes math. Portions of the first edition are available online.
|
email: john@forkosh.com |
|
|