Der Funktionswert f(x0) einer reellen Funktion f mit der Definitionsmenge ID heißt lokales Maximum, wenn es eine Umgebung U(x0) gibt, so dass für alle x
U(x0) 
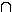ID gilt f(x) ≤ f(x0).Was versteht man unter relativen bzw. lokalen Extrema?
Definition:
Der Funktionswert f(x0) einer reellen Funktion f mit der Definitionsmenge ID heißt lokales Maximum, wenn es eine Umgebung U(x0) gibt, so dass für alle xU(x0) 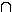ID gilt f(x) ≤ f(x0).
Der Funktionswert f(x0) einer reellen Funktion f mit der Definitionsmenge ID heißt lokales Minimum, wenn es eine Umgebung U(x0) gibt, so dass für alle xU(x0)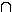ID gilt f(x) ≥ f(x0).
Ein lokales Extremum wird im allgemeinen mit Hilfe der Differentialrechnung bestimmt. (Nullstellen der 1. Ableitung!).
Was ist nun ein "Globales Maximum"?
Unter einem globalen oder absoluten Maximum/Minimum versteht man die Stelle x0, an der die Funktion den größten/kleinsten Wert in ID annimmt.
Bei den Extremwertaufgaben ist meist das lokale Extremum gleichzeitig auch das globale Extremum und damit die gesuchte Lösung.
Mit Zielfunktion soll im Folgenden immer die Funktion bezeichnet werden, deren Extremwerte berechnet werden müssen. Die unabhängige Variable der Zielfunktion muss nicht x sein. Häufig wird eine für das Problem günstige Variable gewählt.