Krummlinig begrenzte Flächen werden zunächst näherungsweise in elementargeometrische Figuren wie z.B. Dreiecke, Quadrate, Rechtecke, Trapeze usw. unterteilt, deren Gesamtfläche dann mit ihrer jeweiligen Formel berechnet wird.
Am bekanntesten ist die „Streifenmethode“, bei der die zu berechnende Fläche mit Hilfe von Rechtecken gleicher Breite unterteilt wird:
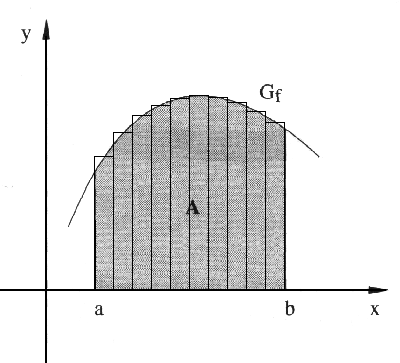
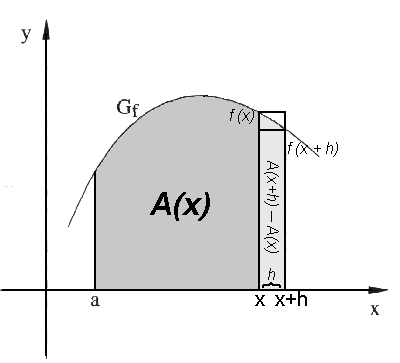
Versuchen wir nun, wie in der Skizze dargestellt, diesen Flächenzuwachs durch zwei Rechtecke, eines, das etwas zu groß, und eines, das etwas zu klein geraten ist, anzunähern. Beide Rechtecke haben die Breite h. Das zu große Rechteck hat die Höhe f(x), das zu kleine die Höhe f(x+h). Es gilt also:
Fläche des kleinen Rechtecks < hellgrauer Streifen < Fläche des großen Rechtecks
Also: h · f(x+h) < A(x+h)– A(x) < h · f(x)
Diese Ungleichungskette besagt, dass der mittlere Term von den beiden Außentermen „eingeklemmt“ wird. Daran ändert sich nichts, wenn man die Ungleichung durch h dividiert:
f(x+h) <
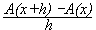< f(x)Ziehen wir nun die „Klemmschraube“ an und lassen h gegen 0 streben. Dann wandert wegen der Stetigkeit von f die linke Seite auf die rechte Seite zu, so dass der mittlere Term dann gleich dem rechten Term wird:
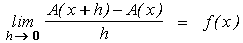
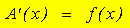
| Die Ableitungsfunktion der Flächenfunktion A ist gleich der Ausgangsfunktion f. |
Eine Funktion, deren Ableitungsfunktion f bekannt ist, heißt „Stammfunktion“ von f. Nun gibt es aber unendlich viele Stammfunktionen von f, denn wenn beispielsweise F(x) eine bestimmte Stammfunktion von f(x) ist, dann ist auch die Funktion
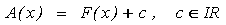
Gott sei Dank lässt sich die Konstante c sogar bestimmen, denn schließlich ist ja bekannt, dass A(a) den Wert Null haben muss. Die Flächenfunktion A misst nämlich die Fläche unter dem Graphen von f ab a, und wenn die Fläche dort auch schon wieder aufhört, entartet sie zur Ordinatenstrecke von f bei a, hat also demzufolge den Wert 0. Wenn wir also a in die letzte Gleichung einsetzen, ergibt sich: 0 = F(a) + c und damit: c =– F(a) .
Setzen wir dieses Resultat und statt x die rechte Intervallgrenze b in die obige umrandete Gleichung ein, so ergibt sich der Hauptsatz der Integralrechnung:
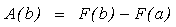
Die Schreibweise A(b) für die Fläche zwischen Gf und der x-Achse im Intervall [a; b] ist nicht ideal, da sie weder die Funktion f enthält, auf der sie basiert, noch den Beginn a der Flächenmessung noch die Variable angibt, nach der die Stammfunktion überhaupt zu bilden ist. Daher verwendet man eine andere, seit Gottfried Wilhelm von Leibniz gebräuchliche Schreibweise:
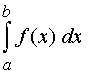
Diese Schreibweise für den Inhalt der Fläche unter dem Graphen einer Funktion f zwischen den Stellen a und b wird als „bestimmtes Integral“ bezeichnet und folgendermaßen gelesen:
„Integral von f(x) dx in den Grenzen von a bis b“ oder „Integral von f(x) dx von a bis b“, auch „Integral über f(x) dx von a bis b“.
f (x) wird als „Integrand“ bezeichnet, a heißt „untere“ und b „obere Integrationsgrenze“ und das Intervall [a, b] wird „Integrationsbereich“ (auch „Integrationsintervall“) genannt. Das Anhängsel „dx“ macht deutlich, dass die Stammfunktion F des Integranden f nach der Variablen x aufgestellt werden muss.
Die Schreibweise des bestimmten Integrals stammt, wie schon erwähnt, von Gottfried Wilhelm von Leibniz. Er hat sich die Fläche unter einem Funktionsgraphen als aus unendlich vielen, unendlich dünnen nebeneinander stehenden Rechtecken mit der Breite dx und der Höhe f(x), also der Fläche f(x)dx zusammengesetzt gedacht, jedes ähnlich einem schmalen Streifen. Der Flächeninhalt wird als "Summe" dieser unendlich vielen, unendlich schmalen Rechtecksflächen dargestellt. Das Integralzeichen als langgestrecktes "S" steht für diese "Summe". Sie erstreckt sich in gewisser Weise "über alle x", beginnend bei a und endend bei b, was oberhalb und unterhalb des Integralzeichens vermerkt wird. In dieser Interpretation ist die Größe f(x) dx, wie die Schreibweise nahe legt, tatsächlich ein Produkt. Die Schreibweise ist aber heutzutage nur mehr symbolisch zu verstehen, hat also den ursprünglichen geometrischen Bezug verloren.
In der Integralschreibweise lautet der Hauptsatz der Integralrechnung:
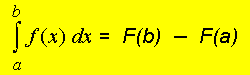
Für den gesamten Rechenvorgang hat sich die Schreibweise
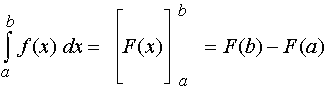
Wegen der Differenz F(b) - F(a) entfällt die Integrationskonstante c. Man kann deshalb beim Bestimmen der Stammfunktion c = 0 wählen.
Im Hauptsatz der Integralrechnung ist F eine Stammfunktion von f, die man durch die Umkehrung der Differentation (Ableitung) der Integrandenfunktion f erhält . Man könnte sagen, statt abzuleiten sucht man die „Aufleitung“.
Das Aufsuchen einer Stammfunktion heißt „Integrieren.“
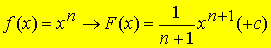
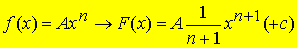
Außerdem darf eine Summe wie z B. eine Polynomfunktion gliedweise integriert werden, denn wir wissen, dass diese Regel auch beim Ableiten gilt.
Gegeben ist die Funktion f mit der Gleichung f (x) = 3x2. In den Grenzen x = 0 bis x = 1 soll die Fläche zwischen dem Graphen von f und der x-Achse ermittelt werden.
Lösung:
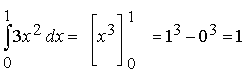
Und so haben wir bereits eine Fläche unter einer Parabel berechnet.
Aufgaben zu Bestimmten Integralen
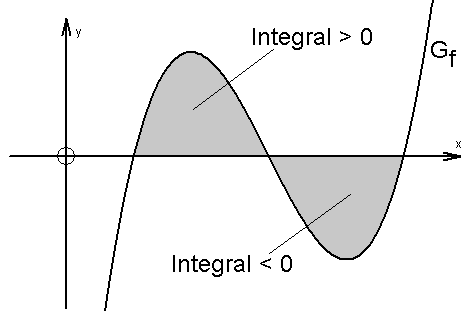
Bisher haben wir nur Funktionen besprochen, die positive Funktionswerte besitzen, d.h. deren Graphen oberhalb der x-Achse liegen. Wird ein solcher Graph durch Multiplikation des Funktionsterms mit –1 an der x-Achse gespiegelt, so dreht sich logischerweise auch die zur Flächenberechnung benutzte Stammfunktion um, so dass jetzt das bestimmte Integral des unterhalb der x-Achse liegenden Flächenstücks einen negativen Wert ergibt. Es gilt also:
Beispiel:
Der Graph der Funktion f(x) = – 3x2 ist eine Parabel unterhalb der x-Achse, und dementsprechend ist das Integral negativ, wenn von links nach rechts integriert wird:
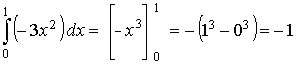
Ist das Integral einer Funktion über einem gegebenen Intervall gleich 0, so sind in diesem Intervall die Flächen oberhalb und unterhalb der x-Achse gleich groß, heben sich also wie z. B. in der letzten Grafik gegenseitig auf.
Werden bei einem bestimmten Integral die Grenzen vertauscht, so ergibt sich nach dem Hauptsatz statt F(b)– F(a) die umgekehrte Differenz F(a)– F(b) , so dass sich der ganze Wert des Integrals umdreht:
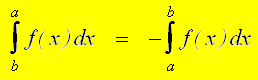
Im Folgenden liegen die zu berechnenden Flächen teilweise oberhalb und teilweise unterhalb der x-Achse. Um zu vermeiden, dass sich diese Flächenstücke bei der Flächenberechnung durch Integration gegenseitig aufheben, müssen sie einzeln, d. h. abschnittsweise bestimmt werden. Das Verfahren wird im Folgenden näher erläutert.
Diese müssen zunächst bestimmt werden.
Danach wird das gesamte Intervall mittels der Nullstellen der Funktion f in Teilintervalle zerlegt.
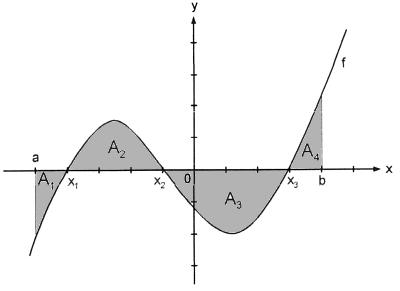
Der gesuchte Flächeninhalt ist die Summe der Beträge der bestimmten Integrale über den Teilintervallen:
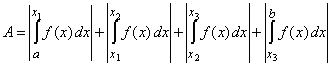
Beim zweiten und vierten Integral könnten die Betragsstriche natürlich weggelassen werden, da der entsprechende Abschnitt des Graphen von f oberhalb der x-Achse verläuft.
Wir fassen zusammen: Bei der Berechnung von Flächeninhalten zwischen einem Graphen und der x-Achse darf nicht über Schnittpunkte mit der x-Achse integriert werden, es sei denn, der Graph berührt dort die x-Achse nur.
Hinweis: Die Notwendigkeit des abschnittweisen Integrierens kommt auch noch in einem ganz anderen Zusammenhang vor:
Bei der Herleitung des Hauptsatzes haben wir vorausgesetzt, dass f stetig ist. Das bedeutet aber nicht, dass nur stetige Funktionen integriert werden können. Soll das bestimmte Integral einer stückweise stetigen Funktion mit Hilfe des Hauptsatzes berechnet werden, so muss jedes Intervall, in dem sie stetig ist, für sich betrachtet werden. Danach wird die Summe dieser Einzelintegrale berechnet.
Beispiel:
In der folgenden Skizze sind die Integrale von a bis b und von b bis c getrennt zu berechnen und danach zu addieren:
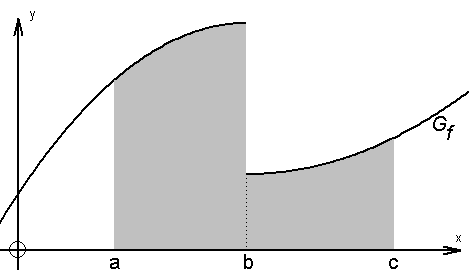
Aufgaben zu Flächen zwischen Graph und x-Achse
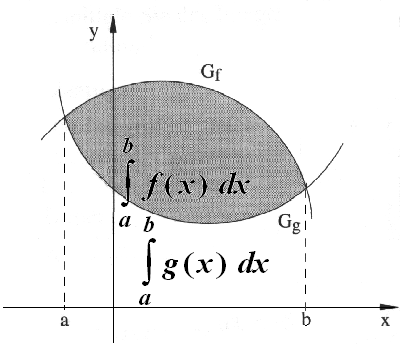
- Wir bestimmen die Schnittstellen a und
b der beiden Funktionen f und g.
- Unter der Voraussetzung, dass im Intervall [a; b]
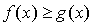, gilt:
getönte Fläche zwischen Gf und Gg =
Fläche von a bis b zwischen Gf und der x-Achse
minus Fläche von a bis b zwischen Gg und der x-Achse =
.
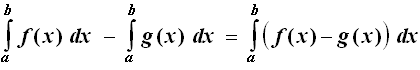Erstes Beispiel:
Die Graphen der Funktionen mit den Gleichungen f(x) = x2 + 2x + 1 und g(x) = – x + 5 schließen eine Fläche ein.
Der Inhalt dieser Fläche ist zu berechnen.
Skizze:
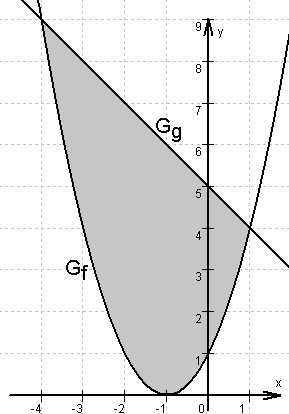
Schnittstellen von f und g:
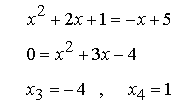
Ansatz zur Flächenberechnung:
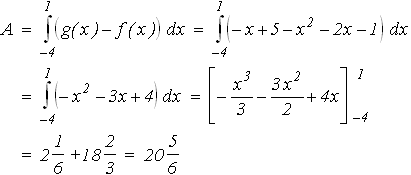
Der gesuchte Flächeninhalt misst
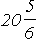Flächeneinheiten.Zweites Beispiel:
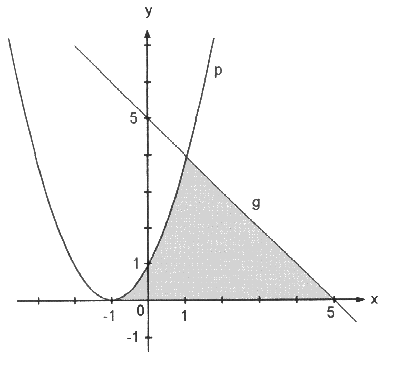
Die Parabel p:
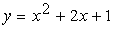und die Gerade g: 
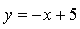begrenzen
mit der x-Ache eine Fläche.Der Inhalt dieser Fläche ist zu berechnen.
Skizze:
Überprüfen auf Nullstellen:
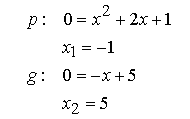
Da die x-Achse die gesuchte Fläche begrenzt, liegt diese Fläche über dem Intervall [-1; 5].
Schnittstelle von p und g im Intervall [-1; 5]:
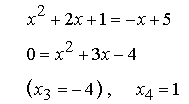
Zur Flächenberechnung wird das Intervall [-1; 5] also in zwei Teilintervalle zerlegt:
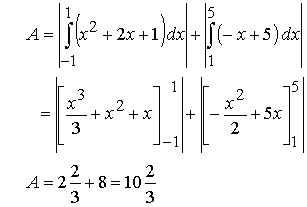
Der gesuchte Flächeninhalt misst
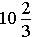Flächeneinheiten.Aufgaben zu Flächen zwischen zwei Funktionsgraphen
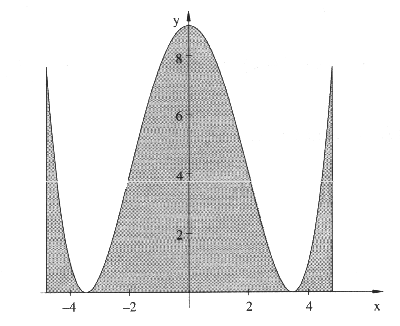
Ist der Graph der Funktion f symmetrisch zur y-Achse und liegen die Integrationsgrenzen ebenfalls symmetrisch zur
.
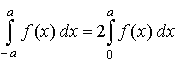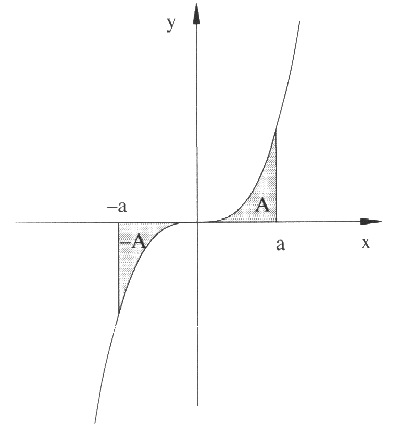
Ist der Graph der Funktion f punktsymmetrisch zum Koordinatenursprung und liegen die Integrationsgrenzen ebenfalls punktsymmetrisch zum Koordinatenursprung, so gilt:
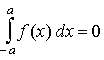.Aufgaben zur Symmetrie