Dies ist ein Beispiel für einen einseitigen Hypothesentest
Aufgabe :
Bei einer automatischen Verpackungsmaschiene, weiß man aus lang andauernden Beobachtungen, dass die Wahrscheinlichkeit für eine vollständige Verpackung mindestens 80% beträgt. Diese Angabe soll nun getestet werden, indem 50 Packungen auf Vollständigkeit überprüft werden.
1. Stellen sie die Null- und die Gegenhypothese auf
Da eine Wahrscheinlichkeit nicht größer als 1 sein kann und die Wahrscheinlichkeit der Nullhypothese mindestens 0,8 ist, muß die Gegenhypothese kleiner als 0,8 sein.
Es gilt : 
2. Stellen sie die Entscheidungsregel auf, wenn der Annahmebereich im Intervall
liegt
Für die Entscheidungsregel benötigen sie den genauen Annahme- und Ablehnungsbereich.
Es gilt :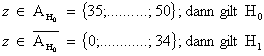 
D.h. wenn
das Ergebnis der Stichprobe in 
fällt,
dann wird 
angenommen,
wenn
das Ergebnis der Stichprobe in 
fällt, wird
abgelehnt.
3. Berechnen sie den Fehler erster Art
Fehler erster Art = alfa-Fehler
D.h.
die
wird abgelehnt, obwohl sie richtig ist.
Da man davon ausgeht,
dass
richtig ist, wird auch mit der Wahrscheinlichkeit von
gerechnet.
wird nur abgelehnt, wenn das Ergebnis der Stichprobe in
fällt, daher berechnet man die Wahrscheinlichkeit von
aus.
n=50, p=0,8, also
ist 
Es gilt : 
(siehe Tabelle)
D.h. mit einer Wahrscheinlichkeit von 0,0308 lehnt man die Nullhypothese ab, obwohl sie richtig ist.
4. Berechnen Sie den Beta-Fehler, wenn die WSK für vollständige Verpackung nur 70% beträgt.
Jetzt ist wieder n=50,
aber p=0,7, also muss mit F50/0,7 gerechnet werden.
Es gilt: 