Beispiel zum Signifikanzniveau
Aufgabe:
Ein Schüler behauptet, dass die Wahrscheinlichkeit, mit der er zu spät zur Schule kommt höchstens 10% beträgt. Kann er mit einem Signifikanzniveau von 20% seine Behauptung noch aufrecht erhalten, wenn er die letzten 30 Schultage 6 mal zu spät gekommen ist?
1. Stellen sie die Null- und die Gegenhypothese auf.
Er behauptet, das er höchstens 10% zu spät kommt, also muß die Nullhypothese kleiner gleich 0,1 sein.
es gilt : 
2. Stellen sie mit Hilfe des Signivikanzniveaus den Ablehnungsbereich auf.
Wir wissen, dass
das Signivikanzniveau
das Ergebnis des 
Fehlers ist und das soll nicht größer als
0,2 sein. Wir wissen auch, dass der Erwartungswert( = 3) im Annahmebereich
enthalten ist, das kann ein Hinweis dafür sein, ob der Annahmebereich
links (also bei 0 anfangend) oder rechts (also bis 30 gehend) liegt.
Ist die Wahrscheinlichkeit der Nullhypothese < als die der Gegenhypothese, liegt der Annahmebereich links.
Ist die Wahrscheinlichkeit der Nullhypothese > als die der Gegenhypothese, liegt der Annahmebereich rechts.
Daraus ergibt sich:
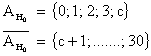
c ist der "kritische Wert", der noch berechnet werden muss.
Wir wissen, wie
man den Fehler erster Art berechnet, nur dass wir jetzt das Ergebnis
der WSK schon haben und c berechnen müssen. Das sieht so aus:
n=30, p=0,1, also ist mit B(30/0,1/k) bzw. F30/0,1 zu rechnen,
der Fehler 1.Art soll höchstens 20% = 0,2 sein,
also gilt: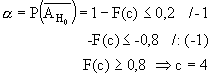 
oder mit den Summen für die Binomialverteilung ausgedrückt:
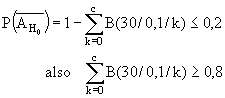
Aus der Tabelle für die Binomialverteilung entnehmen wir den gesuchten
Wert c=4 (gehört zum ersten Wert der Summenspalte, der größer
als 0,8 ist).
Nun gilt :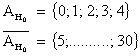 
Er ist 6 mal zu spät zur Schule gekommen in 30 Tagen. Da die 6 schon in den Ablehnungsbereich fällt, kann er seine Behauptung nicht mehr aufrecht erhalten.