Dies ist ein Beispiel zum zweiseitigem Test
Eine Urne enthält 6 Kugeln mit zwei Farben ( schwarz und weiß ). Jemand behauptet es seien 2 schwarze Kugeln darunter. Durch das Entnehmen von 8 Kugeln mit Zurücklegen und das Feststellen der Anzahl an schwarzen Kugeln unter den 8 gezogenen, soll diese Behauptung getestet werden.
1. Stellen sie Null- und Gegenhypothese auf.
Es gilt
: 
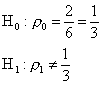
Es wird behauptet, das genau zwei Kugeln schwarz sind und die Wahrscheinlichkeit für genau zwei schwarze Kugeln ist 2/6 also gekürzt 1/3. Ob die Anzahl mehr oder weniger ist, wissen wir nicht, deshalb ist für die Gegenhypothese die WSK ungleich 1/3.
2. Formulieren sie eine vernünftige Entscheidungsregel mit Hilfe des Erwartungswertes.
Der Erwartungswert muß im Annahmebereich enthalten sein, durch das berechnen des Erwartungswertes, läßt sich der Annahmebereich bei dieser Aufgabe ganz gut bestimmen.
Da man nicht genau 2,67 Kugeln ziehen kann, nimmt man 2 und 3 in den Annahmebereich.
3. Berechnen sie den Fehler erster Art und interpretieren sie ihn.
Sieht etwas komplizierter aus, ist es aber nicht. Man muss die Wahrscheinlichkeiten der beiden Ablehnungsbereiche nur zusammen zählen.
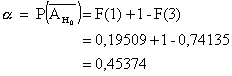
wird mit einer
Wahrscheinlichkeit von 0,45374 abgelehnt, obwohl sie richtig ist -
eine Änderung der Entscheidungsregel wäre zu überlegen.