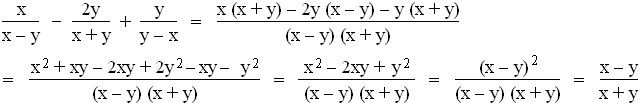1.1        3a (a + b) − (3a − b) b  =  3a2 + 3ab − 3ab + b2  =  3a2 + b2

1.2        



2.          



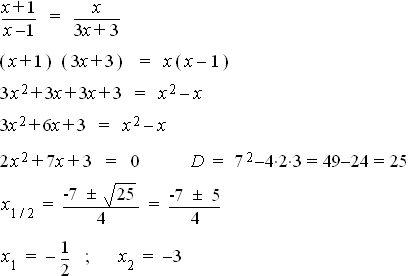3.1        p(x) = –0,5x2 – 6ax – 2,5
             N(1 | 0)  liegt auf der Parabel       p(1) = 0       
             –0,5 – 6a – 2,5 = 0       6a = –3       a = –0,5

3.2        –0,5x2 + 3x – 2,5 = –x – 2,5
             –0,5x2 + 4x = 0
             –0,5x (x – 8) = 0       x1 = 0 ;   x2 = 8
             x1 / 2 in die Geradengleichung       y1 = –2,5 ;   y2 = –10,5
             Die Schnittpunkte sind also  S1(0 | –2,5)  und  S2(8 | –10,5) .

3.3        Koordinaten des Scheitels von  p(x) = –0,5x2 + 3x – 2,5 :
             




	

		

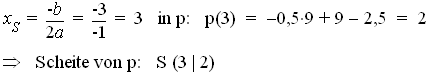
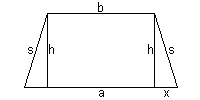
			4.
		
		
a = 1,5 b = b + 2x    

2x = 0,5 b       x = 0,25 b

Nach dem Satz des Pythagoras gilt:

x2 + h2 = s2    

0,0625 b2 + 122 = (b – 7)2

0,0625 b2 + 144 = b2 – 14 b + 49

0,9375 b2 – 14 b – 95 = 0

      D = 142 – 4·0,9375·(–95) = 552,25
		

			
		
	
	

		

			

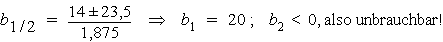Die Seite b ist also 20 cm lang.