| 12. Klasse |
3. Schulaufgabe |
Analysis |
2005/06 |
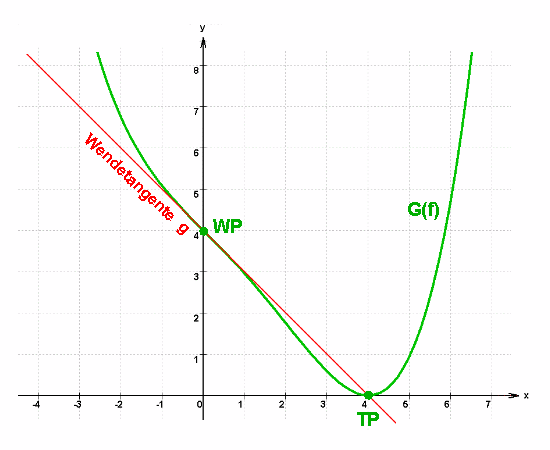
1.0 Vom Graphen einer Polynomfunktion vierten Grades f sei bekannt, dass der Wendepunkt mit der Wendetangente
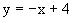 auf der y-Achse liegt und außerdem der Graph den Tiefpunkt ( 4 ; 0 ) besitzt ( siehe Skizze ) .
auf der y-Achse liegt und außerdem der Graph den Tiefpunkt ( 4 ; 0 ) besitzt ( siehe Skizze ) .
 1.1 Ermitteln Sie die Funktionsgleichung von f .
1.1 Ermitteln Sie die Funktionsgleichung von f .
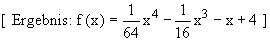 1.2 Der Graph G(f) der Funktion f und dessen Tangente g im Schnittpunkt mit der y-Achse schließen ein Flächenstück ein.
Berechnen Sie dessen Inhalt.
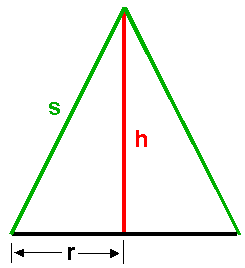
2.0 Die Skizze zeigt den Schnitt eines geraden Kreiskegels, bei dem die Mantellinie s = 15 cm fest vorgegeben ist.
1.2 Der Graph G(f) der Funktion f und dessen Tangente g im Schnittpunkt mit der y-Achse schließen ein Flächenstück ein.
Berechnen Sie dessen Inhalt.
2.0 Die Skizze zeigt den Schnitt eines geraden Kreiskegels, bei dem die Mantellinie s = 15 cm fest vorgegeben ist.
 2.1 Ermitteln Sie die Funktionsgleichung des Kegelvolumens V(h) in Abhängigkeit von der Höhe h
und geben Sie eine sinnvolle Definitionsmenge für V(h) an.
2.1 Ermitteln Sie die Funktionsgleichung des Kegelvolumens V(h) in Abhängigkeit von der Höhe h
und geben Sie eine sinnvolle Definitionsmenge für V(h) an.
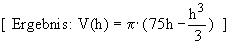 2.2 Ermitteln Sie die Werte für h und r, für die das Kegelvolumen maximal wird. und berechnen Sie das maximale
Volumen.
2.2 Ermitteln Sie die Werte für h und r, für die das Kegelvolumen maximal wird. und berechnen Sie das maximale
Volumen.
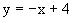 auf der y-Achse liegt und außerdem der Graph den Tiefpunkt ( 4 ; 0 ) besitzt ( siehe Skizze ) .
auf der y-Achse liegt und außerdem der Graph den Tiefpunkt ( 4 ; 0 ) besitzt ( siehe Skizze ) .
 1.1 Ermitteln Sie die Funktionsgleichung von f .
1.1 Ermitteln Sie die Funktionsgleichung von f .
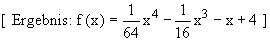 1.2 Der Graph G(f) der Funktion f und dessen Tangente g im Schnittpunkt mit der y-Achse schließen ein Flächenstück ein.
Berechnen Sie dessen Inhalt.
2.0 Die Skizze zeigt den Schnitt eines geraden Kreiskegels, bei dem die Mantellinie s = 15 cm fest vorgegeben ist.
1.2 Der Graph G(f) der Funktion f und dessen Tangente g im Schnittpunkt mit der y-Achse schließen ein Flächenstück ein.
Berechnen Sie dessen Inhalt.
2.0 Die Skizze zeigt den Schnitt eines geraden Kreiskegels, bei dem die Mantellinie s = 15 cm fest vorgegeben ist.
 2.1 Ermitteln Sie die Funktionsgleichung des Kegelvolumens V(h) in Abhängigkeit von der Höhe h
und geben Sie eine sinnvolle Definitionsmenge für V(h) an.
2.1 Ermitteln Sie die Funktionsgleichung des Kegelvolumens V(h) in Abhängigkeit von der Höhe h
und geben Sie eine sinnvolle Definitionsmenge für V(h) an.
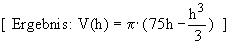 2.2 Ermitteln Sie die Werte für h und r, für die das Kegelvolumen maximal wird. und berechnen Sie das maximale
Volumen.
2.2 Ermitteln Sie die Werte für h und r, für die das Kegelvolumen maximal wird. und berechnen Sie das maximale
Volumen.
