1.4      Die beiden rechten Terme sind gleich, da  a(a + 1) = a2 + a  wie auch   = a2 + a.
              Der linke Term ist kleiner, da  a2 + 1  <   a2 + a,  falls  a > 1.


   2.1      g:   y  =  mx + t 
              A, B  in  g  einsetzen: 
               I.                   2m + t   =   1
              II.                   4m + t   =   2
              II  –  I            2m         =   1
                                      m         =   0,5     in  I:     1 + t   =   1                 t   =   0
                     g:   y  =  0,5x 
              h:   y  =  mx + t 
              C, D  in  h  einsetzen: 
               I.                   –m + t   =    4
              II.                   3m + t   =  –1
              II  –  I            4m         =  –5
                                      m         =  –1,25     in  I:     1,25 + t   =   4                 t   =   2,75
                     h:   y  =  –1,25x + 2,75 
              Schnittansatz  für  g  und  h : 
              0,5x   =   –1,25x + 2,75      | + 1,25x
              1,75x   =   2,75
              x   =   1,571   in  g :       y   =   0,786
                  S(1,571 | 0,786)

   2.2      
              Die Grundseite  g  ist die Strecke zwischen den beiden Nullstellen.  
              Bestimmung der Nullstellen der beiden Geraden : 
              x + 1  =  0       x  =  –1
              –0,5x + 2  =  0       –0,5x  =  –2       x  =  4 
                  Die Grundseite  g  hat die Länge  4 + 1 = 5 LE. 
              Die Höhe  h  ist die Ordinate (d. h. y-Wert) des Geradenschnittpunktes. 
              Bestimmung des Geradenschnittpunktes : 
              x + 1   =   –0,5x + 2      | + 0,5x   – 1
              1,5x   =   1
              x   =                y   =   
                  Die Höhe  h  hat die Länge   LE.
              Damit ergibt sich für den Inhalt  A  der Dreiecksfläche :  
              


   3.        
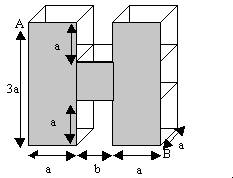   3.1      Volumen  V  des abgebildeten „H-förmigen“ Körpers in Abhängigkeit von  a  und  b : 
              V   =   2 · V(seitliche Säule)  +  V(Mittelstrebe)
                    =   2 · (a2 · 3a)               +  (3a – a – a) · a · b
                    =   6a3   +   a2 b

   3.2      Länge  d  der Strecke  [AB]  in Abhängigkeit von  a  und  b : 
              d2   =   (3a)2 + (a + b + a)2   (Satz des Pythagoras)
                     =   9a2 + (2a + b)2
                     =   9a2 + 4a2 + 4ab + b2
                     =   13a2 + 4ab + b2 
                  d   =   

   3.3      Oberfläche  A  des abgebildeten „H-förmigen“ Körpers in Abhängigkeit von  a  und  b : 
              A   =   2 · A(seitliche Säule)    +  A(Mantel der Mittelstrebe)  –  2 · A(Strebenansatz)
                    =   2 · (2 · a2 + 4 · a · 3a)  +              4 · a · b                   –  2 · a2
                    =   2 · (2a2 + 12a2)  +  4ab  –  2a2
                    =   2 · 14a2  +  4ab  –  2a2
                    =   28a2  +  4ab  –  2a2
                    =   26a2  +  4ab


   

   4.2      x  =  0             y  =  0,5·02 + a·0 + 2  =  2 
              Also schneidet die Parabel  p  die y-Achse bei einem positiven Wert.

   4.3      a  =  1             p:   y  =  0,5x2 + x + 2 
              Skizze: 
              
                  Die gespiegelte Parabel  p*  hat die Gleichung:    y  =  –yp  =  –0,5x2 – x – 2