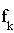 : x
: x 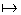
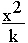 – 2x + k mit k
– 2x + k mit k 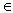 IR \ {0};
IR \ {0}; 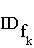 = IR
= IR und
F: x
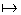
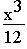 –
– 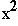 + 4x –
+ 4x – 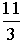 ;
;  = IR .
= IR .
Die Graphen der Funktionen fk und F in einem kartesischen Koordinatensystem heißen Gfk und GF.
Zeigen Sie, dass die Scheitelpunkte aller Parabeln Gfk auf der x-Achse liegen. Geben Sie die Wertemenge Wk der Funktion fk in Abhängigkeit von k an. (5 BE)
Zeichnen Sie für den Sonderfall k = 4 die Parabel Gf4 für 0 ≤ x ≤ 8. Verwenden Sie dazu eine gesonderte DIN-A4-Seite im Hochformat mit der x-Achse in der Seitenmitte.
Maßstab auf beiden Achsen: 1 LE = 1 cm. (3 BE)
Zeigen Sie, dass für einen geeigneten Wert von k die Funktion F eine Stammfunktion der zugehörigen Funktion fk ist.
Bestimmen Sie außerdem das Monotonieverhalten der Stammfunktion F. Untersuchen Sie, ob der Graph GF relative Extrempunkte besitzt. (6 BE)
Ermitteln Sie die Koordinaten des Wendepunktes des Graphen GF.
Welche besondere Eigenschaft hat dieser Wendepunkt? (4 BE)
Weisen Sie nach, dass sich die Graphen Gf4 und GF im Punkt P(2; yP) senkrecht schneiden und dass der Punkt P der einzige Punkt ist, den die beiden Graphen gemeinsam haben. (9 BE)
Zeichnen Sie den Graphen GF mit Hilfe bisheriger Ergebnisse und einer geeigneten Wertetabelle für 0 ≤ x ≤ 8 in das unter Teilaufgabe 1.1.2 beschriebene Koordinatensystem ein. (5 BE)
Die y-Achse und die Graphen Gf4 und GF begrenzen im I. und IV. Quadranten des Koordinatensystems ein Flächenstück. Berechnen Sie die Maßzahl seines Flächeninhalts. (6 BE)
1.3.0
Der Graph  der reellen Funktion g: x
der reellen Funktion g: x  g(x);
g(x); 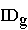 = IR mit
= IR mit
g(x) = 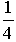 (–x
(–x + ax
+ ax + bx + c) schneidet die x-Achse an der Stelle x
+ bx + c) schneidet die x-Achse an der Stelle x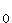 = 2
= 2
und hat den relativen Tiefpunkt T(4; –5).
Bestimmen Sie den Funktionsterm g(x). (7 BE)
Mit den Angaben für f4(x) und F(x) aus 1.0 gilt für den Funktionsterm g(x) die folgende Beziehung: g(x) = 3(f4(x) – F(x)) (Beweis nicht erforderlich).
Es sei xH die Abszisse des Hochpunktes H des Graphen Gg. Beweisen Sie nur mit Hilfe der eben genannten Beziehung, ohne die Stelle xH zu berechnen, die folgende Aussage:
"An der Stelle xH haben die Graphen Gf4 und GF parallele Tangenten."
Begründen Sie auch ohne Rechnung, dass diese parallelen Tangenten nicht zusammenfallen können. (4 BE)
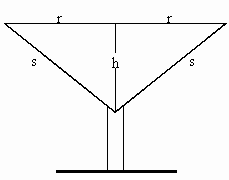 Der Kelch eines Eisbechers soll die Form eines auf der Spitze stehenden geraden Kreiskegels erhalten (siehe Skizze des Achsenschnittes; die Dicke der Glaswand werde vernachlässigt). Die Längenmaßzahl der Mantellinie s des Kegels beträgt 12.
Der Kelch eines Eisbechers soll die Form eines auf der Spitze stehenden geraden Kreiskegels erhalten (siehe Skizze des Achsenschnittes; die Dicke der Glaswand werde vernachlässigt). Die Längenmaßzahl der Mantellinie s des Kegels beträgt 12.
Stellen Sie die Volumenmaßzahl V(h) des Kegels in Abhängigkeit von der Kegelhöhe h dar und geben Sie die Definitionsmenge
I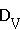 der Funktion V: h
der Funktion V: h 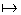 V(h) an.
V(h) an.
Weisen Sie nach, dass die Volumenmaßzahl V(h) für 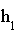 =
= 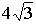 ihren absolut größten Wert annimmt. Zeigen Sie außerdem, dass in diesem Fall die Längenmaßzahlen von Radius r und Höhe h des Kegels im Verhältnis
ihren absolut größten Wert annimmt. Zeigen Sie außerdem, dass in diesem Fall die Längenmaßzahlen von Radius r und Höhe h des Kegels im Verhältnis 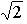 : 1 stehen.
: 1 stehen.
(Mögliches Teilergebnis: V(h) = 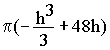 ) (11 BE)
) (11 BE)

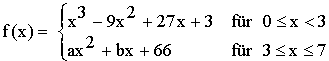
 IR .
IR .