Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2001
A I: Lösungen
1.1.1 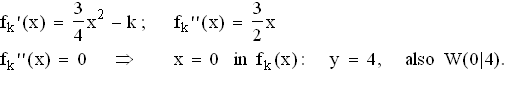 W ist Wendepunkt eines jeden Grafen von fk,
weil seine Koordinaten parameterunabhängig sind.
1.1.2
W ist Wendepunkt eines jeden Grafen von fk,
weil seine Koordinaten parameterunabhängig sind.
1.1.2 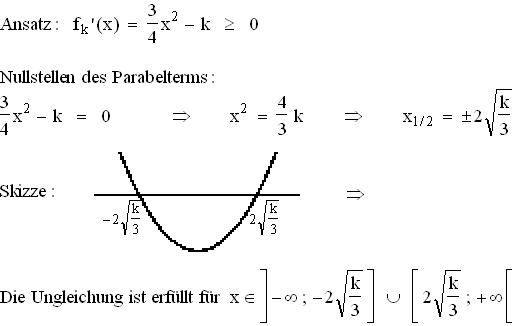 1.1.3 W liegt auf der Geraden, da 4 = –3·0 + 4 gilt.
Kann f
1.1.3 W liegt auf der Geraden, da 4 = –3·0 + 4 gilt.
Kann f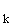 an der Wendestelle, also bei x = 0, die Steigung der Geraden,
also m = –3 haben?
an der Wendestelle, also bei x = 0, die Steigung der Geraden,
also m = –3 haben?
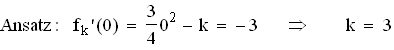 Also ist für k = 3 die Gerade y = –3 x + 4 die Wendetangente des
zugehörigen Schargrafen.
1.2.1
Also ist für k = 3 die Gerade y = –3 x + 4 die Wendetangente des
zugehörigen Schargrafen.
1.2.1 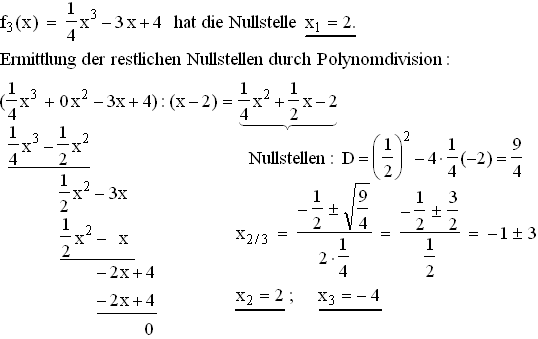 x = 2 ist also eine doppelte, x = –4 eine einfache Nullstelle von f3.
Daraus ergibt sich die Linearfaktorzerlegung:
x = 2 ist also eine doppelte, x = –4 eine einfache Nullstelle von f3.
Daraus ergibt sich die Linearfaktorzerlegung: 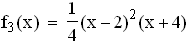 1.2.2 Da nach Aufgabe 1.1.2 die Funktion f
1.2.2 Da nach Aufgabe 1.1.2 die Funktion f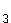 in den Intervallen ]–∞ ; –2]
und [2 ; +∞[ echt monoton zunimmt, müssen bei x = –2 ein Hochpunkt
und bei x = 2 ein Tiefpunkt vorliegen. Nach Einsetzen dieser Abszissenwerte
in die Funktionsgleichung von f
in den Intervallen ]–∞ ; –2]
und [2 ; +∞[ echt monoton zunimmt, müssen bei x = –2 ein Hochpunkt
und bei x = 2 ein Tiefpunkt vorliegen. Nach Einsetzen dieser Abszissenwerte
in die Funktionsgleichung von f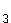 ergibt sich:
HOP(–2 | 8) ; TIP(2 | 0).
Wertetabelle:
ergibt sich:
HOP(–2 | 8) ; TIP(2 | 0).
Wertetabelle:
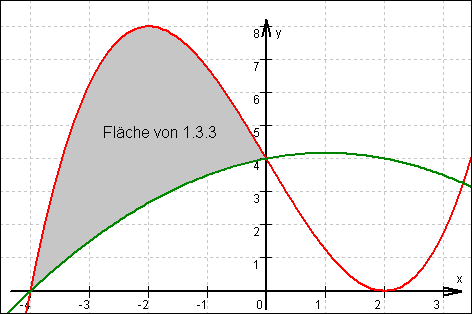
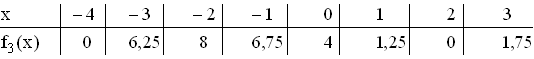 Grafen von f3 und von p (Aufgabe 1.3.2):
Grafen von f3 und von p (Aufgabe 1.3.2):
 1.3.1 Ansatz: p(x) = a x2 + b x + c
1.3.1 Ansatz: p(x) = a x2 + b x + c  p '(x) = 2a x + b
I. p(0) = 4
p '(x) = 2a x + b
I. p(0) = 4  c = 4
II. p(–4) = 0
c = 4
II. p(–4) = 0  16a – 4b + 4 = 0
III. p '(0) =
16a – 4b + 4 = 0
III. p '(0) =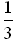
 b =
b =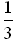 in II:
in II:
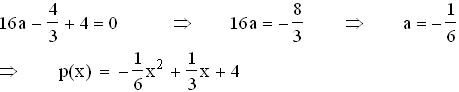 1.3.2
1.3.2 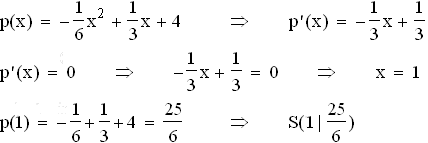 1.3.3
1.3.3 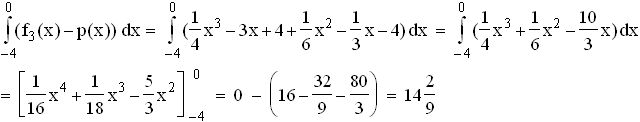 1.4.1
1.4.1 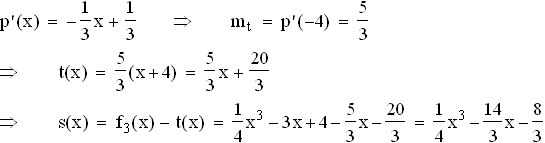 1.4.2
1.4.2  2.1
2.1 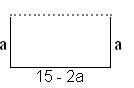
 A(a) = a (15 – 2a) = 15a – 2a
A(a) = a (15 – 2a) = 15a – 2a ,
, 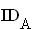 = ] 0 ; 7,5 [.
2.2
= ] 0 ; 7,5 [.
2.2 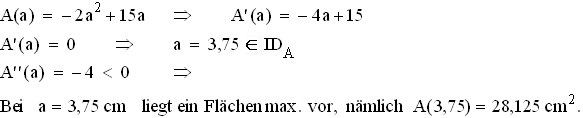
A II: Lösungen
1.1.1 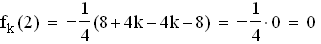
 x
x = 2 ist eine parameterunabhängige Nullstelle von f
= 2 ist eine parameterunabhängige Nullstelle von f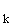 .
.
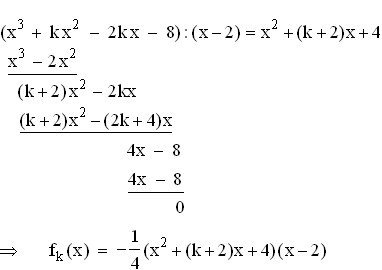 1.1.2
1.1.2 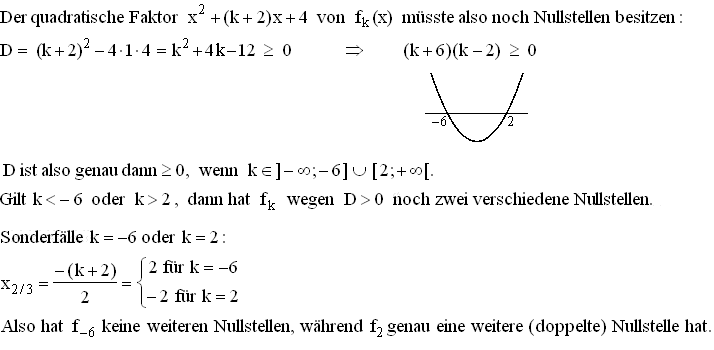 1.1.3
1.1.3 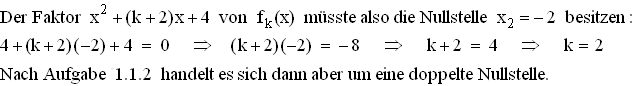 1.2.1
1.2.1  1.2.2
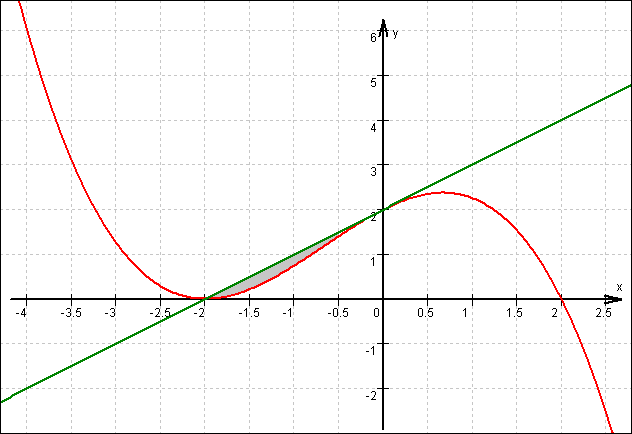
1.2.2 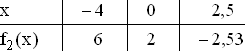 Graf von f2 und t1 (Aufgabe 1.2.4):
Graf von f2 und t1 (Aufgabe 1.2.4):
 1.2.3
1.2.3 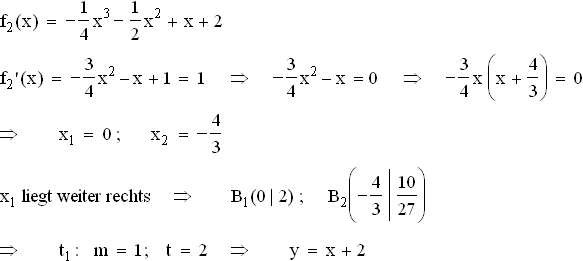 1.2.4
1.2.4 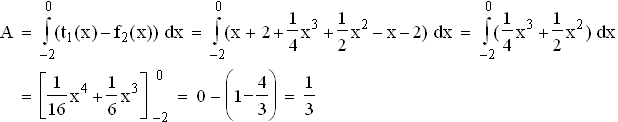 1.3
1.3 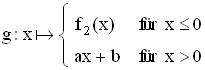 soll bei x = 0 stetig und differenzierbar sein
soll bei x = 0 stetig und differenzierbar sein  I. Die Funktionswerte der „Äste“ müssen bei x = 0 übereinstiimmen
I. Die Funktionswerte der „Äste“ müssen bei x = 0 übereinstiimmen  f2(0) = a·0 + b
f2(0) = a·0 + b  b = 2
II. Die Steigungen der „Äste“ müssen bei x = 0 übereinstiimmen
b = 2
II. Die Steigungen der „Äste“ müssen bei x = 0 übereinstiimmen  f2'(0) = a
f2'(0) = a  a = 1
2.1 E = Kinokartenpreis · Anzahl der Besucher
a = 1
2.1 E = Kinokartenpreis · Anzahl der Besucher  E(x) = (10 + x) (200 – 10x) = –10 x2 + 100 x + 2000 , IDE = [0 ; 20].
2.2 E '(x) = –20 x + 100 = 0
E(x) = (10 + x) (200 – 10x) = –10 x2 + 100 x + 2000 , IDE = [0 ; 20].
2.2 E '(x) = –20 x + 100 = 0  x = 5
x = 5  IDE !
E ''(x) = –20 < 0
IDE !
E ''(x) = –20 < 0  Für eine Preiserhöhung um 5 DM nehmen die Einnahmen den größten Wert an.
(Ein Randmaximum scheidet aus, da zwischen den Rändern der Definitionsmenge von E
und der Stelle x = 5 keine Minimalstellen existieren.)
Für eine Preiserhöhung um 5 DM nehmen die Einnahmen den größten Wert an.
(Ein Randmaximum scheidet aus, da zwischen den Rändern der Definitionsmenge von E
und der Stelle x = 5 keine Minimalstellen existieren.)
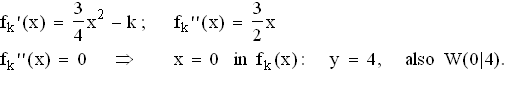 W ist Wendepunkt eines jeden Grafen von fk,
weil seine Koordinaten parameterunabhängig sind.
1.1.2
W ist Wendepunkt eines jeden Grafen von fk,
weil seine Koordinaten parameterunabhängig sind.
1.1.2 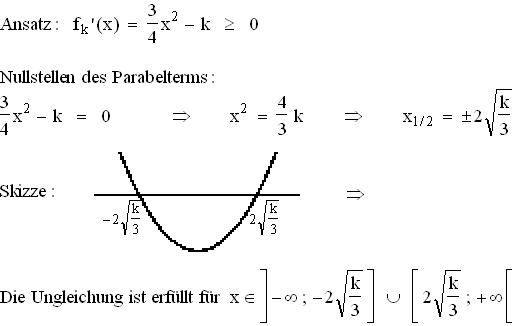 1.1.3 W liegt auf der Geraden, da 4 = –3·0 + 4 gilt.
Kann f
1.1.3 W liegt auf der Geraden, da 4 = –3·0 + 4 gilt.
Kann f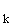 an der Wendestelle, also bei x = 0, die Steigung der Geraden,
also m = –3 haben?
an der Wendestelle, also bei x = 0, die Steigung der Geraden,
also m = –3 haben?
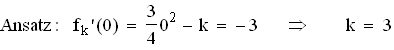 Also ist für k = 3 die Gerade y = –3 x + 4 die Wendetangente des
zugehörigen Schargrafen.
1.2.1
Also ist für k = 3 die Gerade y = –3 x + 4 die Wendetangente des
zugehörigen Schargrafen.
1.2.1 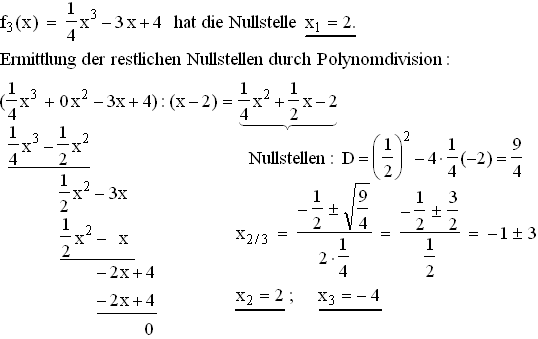 x = 2 ist also eine doppelte, x = –4 eine einfache Nullstelle von f3.
Daraus ergibt sich die Linearfaktorzerlegung:
x = 2 ist also eine doppelte, x = –4 eine einfache Nullstelle von f3.
Daraus ergibt sich die Linearfaktorzerlegung: 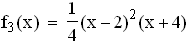 1.2.2 Da nach Aufgabe 1.1.2 die Funktion f
1.2.2 Da nach Aufgabe 1.1.2 die Funktion f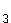 in den Intervallen ]–∞ ; –2]
und [2 ; +∞[ echt monoton zunimmt, müssen bei x = –2 ein Hochpunkt
und bei x = 2 ein Tiefpunkt vorliegen. Nach Einsetzen dieser Abszissenwerte
in die Funktionsgleichung von f
in den Intervallen ]–∞ ; –2]
und [2 ; +∞[ echt monoton zunimmt, müssen bei x = –2 ein Hochpunkt
und bei x = 2 ein Tiefpunkt vorliegen. Nach Einsetzen dieser Abszissenwerte
in die Funktionsgleichung von f ergibt sich:
HOP(–2 | 8) ; TIP(2 | 0).
Wertetabelle:
ergibt sich:
HOP(–2 | 8) ; TIP(2 | 0).
Wertetabelle:
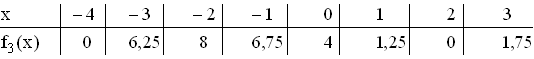 Grafen von f3 und von p (Aufgabe 1.3.2):
Grafen von f3 und von p (Aufgabe 1.3.2):
 1.3.1 Ansatz: p(x) = a x2 + b x + c
1.3.1 Ansatz: p(x) = a x2 + b x + c  p '(x) = 2a x + b
I. p(0) = 4
p '(x) = 2a x + b
I. p(0) = 4  c = 4
II. p(–4) = 0
c = 4
II. p(–4) = 0  16a – 4b + 4 = 0
III. p '(0) =
16a – 4b + 4 = 0
III. p '(0) =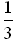
 b =
b =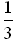 in II:
in II:
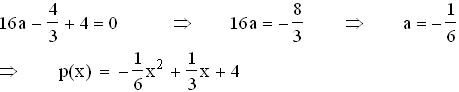 1.3.2
1.3.2 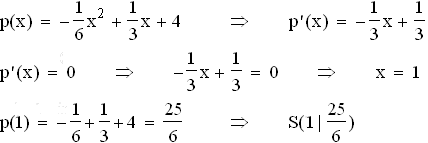 1.3.3
1.3.3 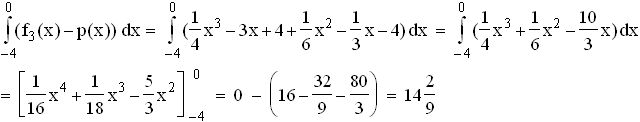 1.4.1
1.4.1 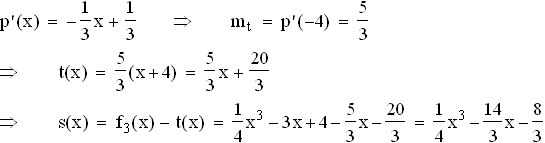 1.4.2
1.4.2  2.1
2.1 
 A(a) = a (15 – 2a) = 15a – 2a
A(a) = a (15 – 2a) = 15a – 2a ,
, 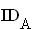 = ] 0 ; 7,5 [.
2.2
= ] 0 ; 7,5 [.
2.2 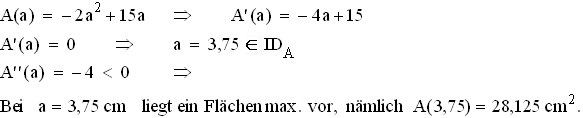
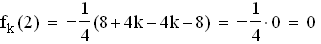
 = 2 ist eine parameterunabhängige Nullstelle von f
= 2 ist eine parameterunabhängige Nullstelle von f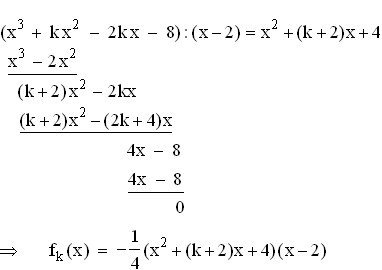 1.1.2
1.1.2 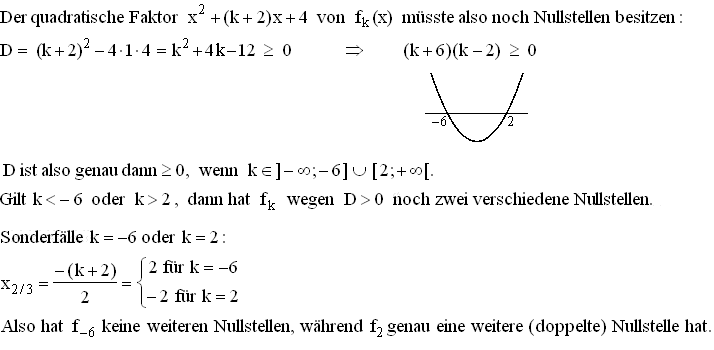 1.1.3
1.1.3 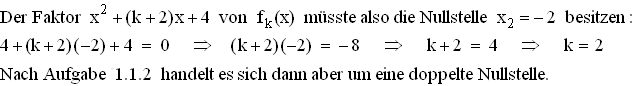 1.2.1
1.2.1  1.2.2
1.2.2 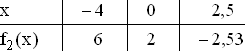 Graf von f2 und t1 (Aufgabe 1.2.4):
Graf von f2 und t1 (Aufgabe 1.2.4):
 1.2.3
1.2.3 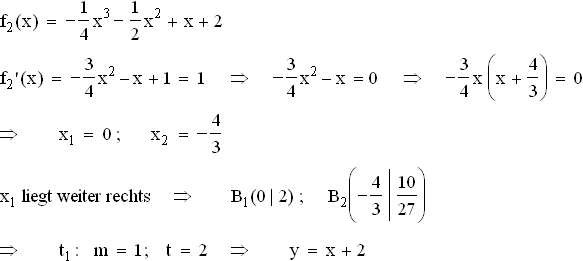 1.2.4
1.2.4 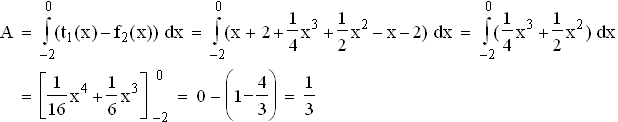 1.3
1.3 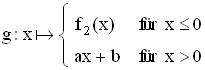 soll bei x = 0 stetig und differenzierbar sein
soll bei x = 0 stetig und differenzierbar sein  IDE !
E ''(x) = –20 < 0
IDE !
E ''(x) = –20 < 0