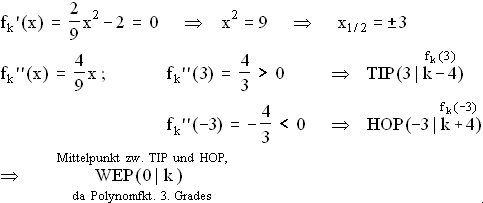 1.2
1.2 Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2002
A I: Lösungen
1.11.2
| k < | –4 | < k < | 4 | < k | |
|---|---|---|---|---|---|
| Lage der Extrempunkte | beide unterhalb der x-Achse | HOP auf der x-Achse | x-Achse zw. beiden | TIP auf der x-Achse | beide oberhalb der x-Achse |
| Anzahl der Nullstellen | 1 | 2 | 3 | 2 | 1 |
2.1 f5(–7) = –6,41 < 0 ; f5(–6) = 1 > 0Zwischen x = –7 und x = –6 muss eine Nullstelle liegen. Bestimmung der Nullstelle mit dem Newton-Verfahren (Startwert: x0 = –6,5) :
2.2
| x | –6,5 | –6 | –5 | –4 | –3 | –2 | –1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 6,5 |
| f5(x) | –2,3 | 1 | 5,7 | 8,3 | 9 | 8,4 | 6,9 | 5 | 3,1 | 1,6 | 1 | 1,7 | 4,3 | 9 | 12,3 |
3.1 Gp berührt den Grafen von f5 in dessen Tiefpunkt (3 | 1)
p(3) = 1
p'(3) = 0, d. h. der TIP des Grafen von f5 ist der Scheitel von Gp
Ansatz für p: p(x) = a(x – 3)2 + 1 Da der Hochpunkt des Grafen von f5 auf Gp liegt, gilt: p(–3) = 9
a(–3 – 3)2 + 1 = 9
36a = 8
a =
in p

3.2.1 Schnittansatz:
3.2.2 Einsetzen von m = 1 in die Gleichung ( * ) sowie in die Diskriminante D von Aufgabe 3.2.1:
Die Fläche zwischen den Grafen von g1 und p beträgt 15,625 FE. 4.1 Da sich bei der Funktion f–4(x) gegenüber f5(x) nur die Konstante um 9 verringert, geht ihr Graf aus dem der Funktion f5 durch Verschiebung um 9 nach unten hervor. Also liegt der Hochpunkt ihres Grafen jetzt auf der x-Achse, so dass bei x = –3 eine doppelte Nullstelle vorliegt. Die noch existierende einfache Nullstelle x = 6 ergibt sich entweder aus der Wertetabelle von Aufgabe 2.2 oder durch Polynomdivision. Dabei kann man gleich durch (x + 3)2, also durch x2 + 6x + 9 dividieren, da die Nullstelle x = –3 ja doppelt vorliegt:
4.2 Da die Funktionswerte F–4'(x) = f–4(x) in ]–∞ ; 6] negativ oder null sind, nimmt F–4 in diesem Intervall echt monoton ab. Im Intervall [6 ; +∞[ hingegen sind die Werte von f–4 positiv oder null, so dass F–4 hier echt monoton zunimmt. Also hat der Graf von F–4 an der Stelle x = 6 einen Tiefpunkt und daher dort auch eine horizontale Tangente. Eine weitere horizontale Tangente hat er bei x = –3, der zweiten Nullstelle von f–4. Da es sich hier um eine doppelte Nullstelle handelt, ist dieser Horizontalpunkt des Grafen von F–4 ein Terrassenpunkt.
A II: Lösungen
1.11.2
1.3
2.1 x1 = 4 ist eine einfache, x2 / 3 = –2 eine doppelte Nullstelle. 2.2
2.3
| x | –5 | –4 | –3 | –2 | –1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f4(x) | 10,1 | 4 | 0,9 | 0 | 0,6 | 2 | 3,4 | 4 | 3,1 | 0 | –6,1 |
3.1 Der rechte Ast dieser abschnittsweise definierten Funktion g heiße p. Der linke Ast von g ist identisch mit f4, d. h. es gilt: g(x) = f4(x) für x
]–∞ ; 0 [. Also ist die Funktion g bei x0 = 0 genau dann stetig und differenzierbar, wenn gilt: I. p(0) = f4(0)
s = 2 II. p'(0) = f4'(0)
r = 1,5 (denn: p'(x) = 2qx + r ; f4'(x) siehe Aufgabe 2.2) Da noch P(4 | 0)
Gp (x = 4 ≥ 0 !) gefordert ist, muss zusätzlich gelten: III. p(4) = 0
16q + 4r + s = 0
16q + 6 + 2 = 0
q = –0,5 . 3.2 Für x < 0 ist g identisch mit f4, hat dort also nur die doppelte Nullstelle x = –2. Für x ≥ 0 ist g identisch mit der quadratischen Funktion p, die in diesem Bereich nur die Nullstelle x = 4 besitzt. Also hat die Funktion g genau zwei Nullstellen. 3.3
Die Maßzahl des Flächenstücks beträgt ca. 10,83 FE. 4.1
4.2 V(h) = π (–0,25 h3 + 36 h)
(2r)2 + h2 = 122 4r2 + h2 = 144
r2 = 36 – 0,25 h2
V(r , h) = r2 π · h
V(h) = (36 – 0,25 h2) π · h
= π (–0,25 h3 + 36 h) ;
IDV = ] 0 ; 12 [V '(h) = π (–0,75 h2 + 36) V '(h) = 0
–0,75 h2 + 36 = 0
h2 = 48
h = ± 4
Da h in IDV liegen muss, gilt h = 4
Beweis, dass für h = 4
das Zylindervolumen maximal wird: V ''(h) = π (–1,5 h) ; V ''(4
) < 0
Das Zylindervolumen wird für h = 4
dm maximal. r2 = 36 – 0,25·48 = 24
r = 2
[dm]. Vmax = V(4
) = π (–0,25·48·4
+ 36·4
) = π (–48
+ 144
) = 96 π
[dm3].