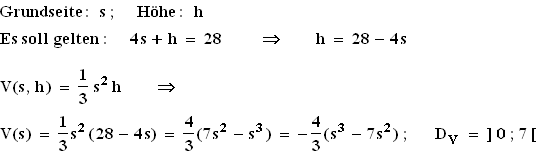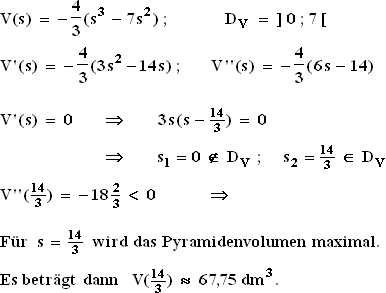Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2003
A I: Lösungen
1.1 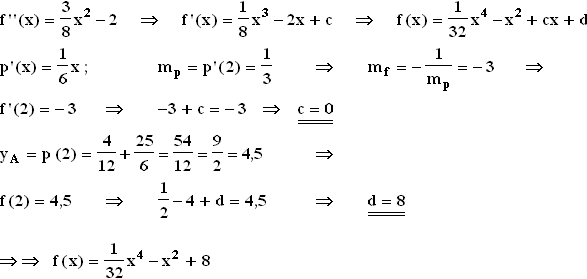 1.2 f hat nur gerade Exponenten
1.2 f hat nur gerade Exponenten  Gf ist achsensymmetrisch zur y-Achse.
1.3 Nullstellen von f :
Gf ist achsensymmetrisch zur y-Achse.
1.3 Nullstellen von f :
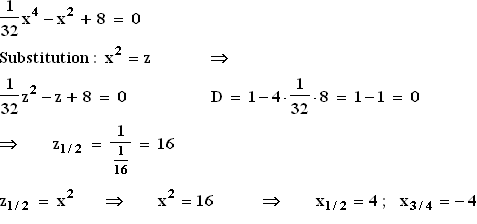 Beide sind also doppelte Nullstellen von f.
1.4
Beide sind also doppelte Nullstellen von f.
1.4  1.5
1.5 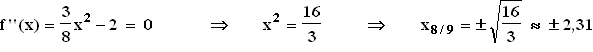 Krümmungsintervalle von Gf :
Gf ist genau dann linksgekrümmt, wenn f ''(x) > 0 .
Da Gf '' eine nach oben geöffnete Parabel ist,
gilt f ''(x) > 0 in ] –∞ ; –2,31 [ und in ] 2,31 ; ∞ [ .
Gf ist genau dann rechtsgekrümmt, wenn f ''(x) < 0 .
Das ist in ] –2,31 ; 2,31 [ der Fall.
Also liegen zwei Wendepunkte vor:
f (± 2,31) = 3,55
Krümmungsintervalle von Gf :
Gf ist genau dann linksgekrümmt, wenn f ''(x) > 0 .
Da Gf '' eine nach oben geöffnete Parabel ist,
gilt f ''(x) > 0 in ] –∞ ; –2,31 [ und in ] 2,31 ; ∞ [ .
Gf ist genau dann rechtsgekrümmt, wenn f ''(x) < 0 .
Das ist in ] –2,31 ; 2,31 [ der Fall.
Also liegen zwei Wendepunkte vor:
f (± 2,31) = 3,55  WEP1/2( ± 2,31 | 3,55 )
1.6 Grafen von f und p :
WEP1/2( ± 2,31 | 3,55 )
1.6 Grafen von f und p :
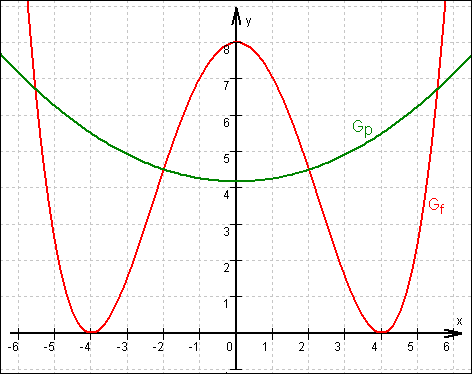 1.7 Nach Aufgabe 1.1 schneiden sich beide Grafen bei x = 2
1.7 Nach Aufgabe 1.1 schneiden sich beide Grafen bei x = 2 
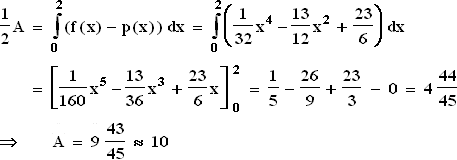 2.1
2.1 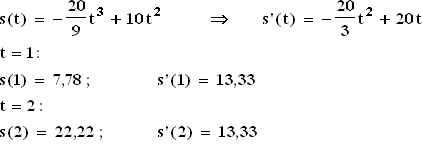 Nach 1 Minute hat die Schnecke mit einer Momentangeschwindigkeit von 13,33 cm/min also 7,78 cm zurückgelegt;
nach 2 Minuten hat sie mit derselben Momentangeschwindigkeit 22,22 cm zurückgelegt.
2.2 Die Schnecke erreicht ihre größte Geschwindigkeit dann, wenn s''(t) = 0 und s'''(t) < 0 .
Nach 1 Minute hat die Schnecke mit einer Momentangeschwindigkeit von 13,33 cm/min also 7,78 cm zurückgelegt;
nach 2 Minuten hat sie mit derselben Momentangeschwindigkeit 22,22 cm zurückgelegt.
2.2 Die Schnecke erreicht ihre größte Geschwindigkeit dann, wenn s''(t) = 0 und s'''(t) < 0 .
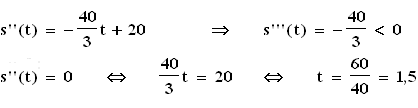 Die Schnecke erreicht ihre größte Geschwindigkeit nach 1,5 Minuten.
Diese Geschwindigkeit beträgt s'(1,5) = 15 cm / min .
3.1
Die Schnecke erreicht ihre größte Geschwindigkeit nach 1,5 Minuten.
Diese Geschwindigkeit beträgt s'(1,5) = 15 cm / min .
3.1 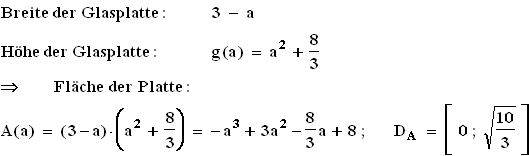 3.2
3.2 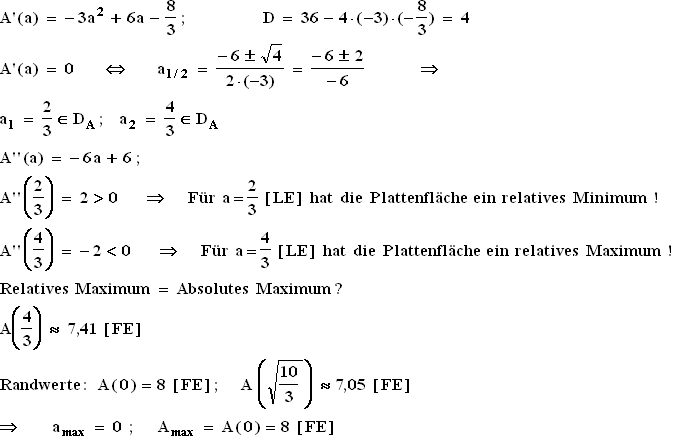
A II: Lösungen
1.1 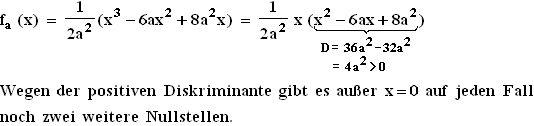 1.2
1.2 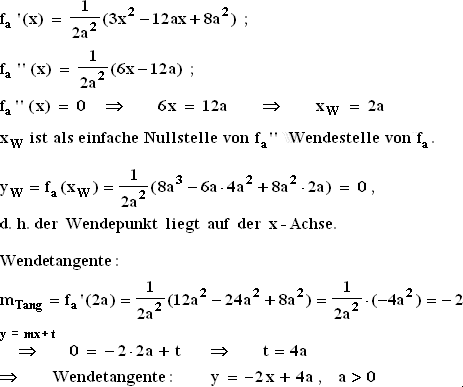 1.3.1
1.3.1 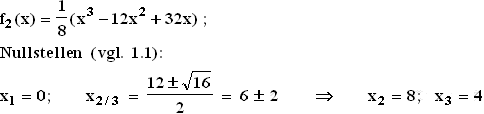 1.3.2
1.3.2 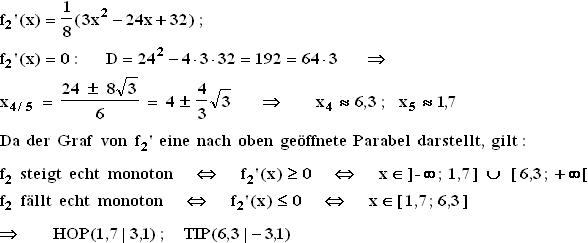 1.3.3 Graf von f2 mit seiner Wendetangente und Graf von p :
1.3.4
2.3
1.3.3 Graf von f2 mit seiner Wendetangente und Graf von p :
1.3.4
2.3 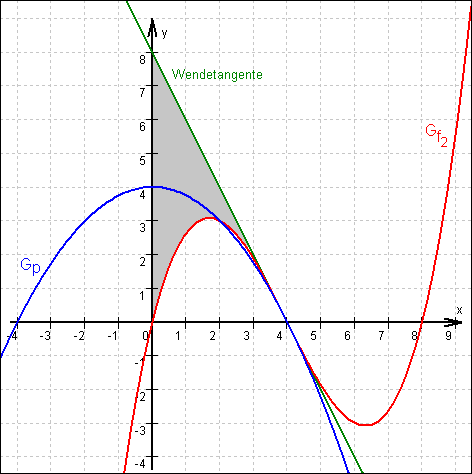 1.4
1.4 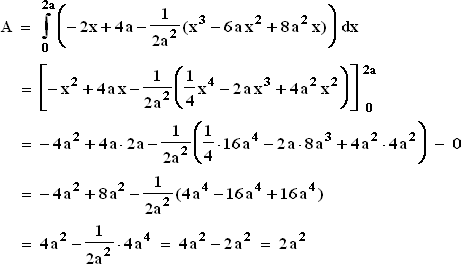 2.1
2.1 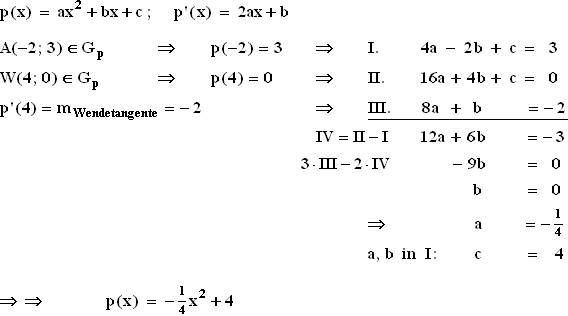 2.2
2.2  3.1 28 = 14 + 7 + 4 + 2 + 1
3.2.1
3.1 28 = 14 + 7 + 4 + 2 + 1
3.2.1 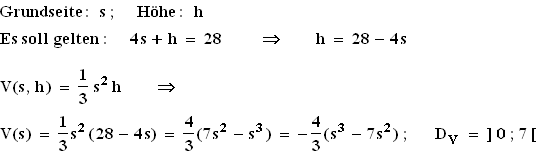 3.2.2
3.2.2 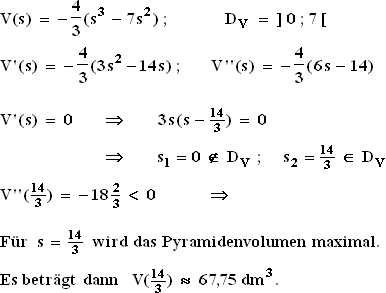
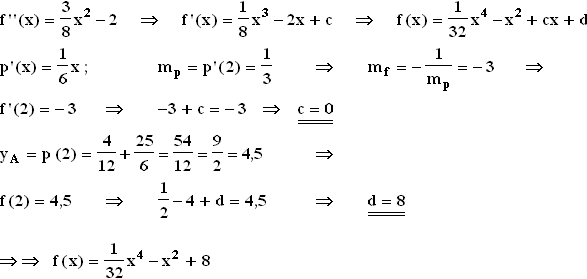 1.2 f hat nur gerade Exponenten
1.2 f hat nur gerade Exponenten  Gf ist achsensymmetrisch zur y-Achse.
1.3 Nullstellen von f :
Gf ist achsensymmetrisch zur y-Achse.
1.3 Nullstellen von f :
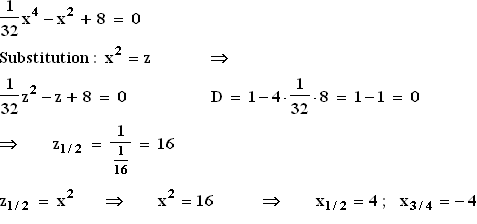 Beide sind also doppelte Nullstellen von f.
1.4
Beide sind also doppelte Nullstellen von f.
1.4  1.5
1.5 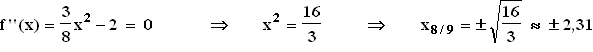 Krümmungsintervalle von Gf :
Gf ist genau dann linksgekrümmt, wenn f ''(x) > 0 .
Da Gf '' eine nach oben geöffnete Parabel ist,
gilt f ''(x) > 0 in ] –∞ ; –2,31 [ und in ] 2,31 ; ∞ [ .
Gf ist genau dann rechtsgekrümmt, wenn f ''(x) < 0 .
Das ist in ] –2,31 ; 2,31 [ der Fall.
Also liegen zwei Wendepunkte vor:
f (± 2,31) = 3,55
Krümmungsintervalle von Gf :
Gf ist genau dann linksgekrümmt, wenn f ''(x) > 0 .
Da Gf '' eine nach oben geöffnete Parabel ist,
gilt f ''(x) > 0 in ] –∞ ; –2,31 [ und in ] 2,31 ; ∞ [ .
Gf ist genau dann rechtsgekrümmt, wenn f ''(x) < 0 .
Das ist in ] –2,31 ; 2,31 [ der Fall.
Also liegen zwei Wendepunkte vor:
f (± 2,31) = 3,55  WEP1/2( ± 2,31 | 3,55 )
1.6 Grafen von f und p :
WEP1/2( ± 2,31 | 3,55 )
1.6 Grafen von f und p :
 1.7 Nach Aufgabe 1.1 schneiden sich beide Grafen bei x = 2
1.7 Nach Aufgabe 1.1 schneiden sich beide Grafen bei x = 2 
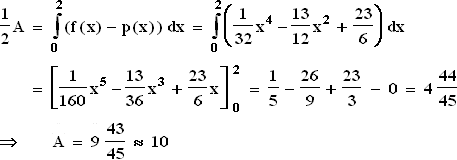 2.1
2.1 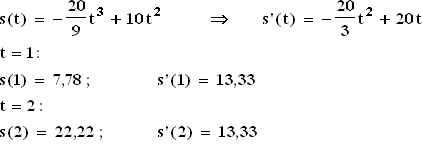 Nach 1 Minute hat die Schnecke mit einer Momentangeschwindigkeit von 13,33 cm/min also 7,78 cm zurückgelegt;
nach 2 Minuten hat sie mit derselben Momentangeschwindigkeit 22,22 cm zurückgelegt.
2.2 Die Schnecke erreicht ihre größte Geschwindigkeit dann, wenn s''(t) = 0 und s'''(t) < 0 .
Nach 1 Minute hat die Schnecke mit einer Momentangeschwindigkeit von 13,33 cm/min also 7,78 cm zurückgelegt;
nach 2 Minuten hat sie mit derselben Momentangeschwindigkeit 22,22 cm zurückgelegt.
2.2 Die Schnecke erreicht ihre größte Geschwindigkeit dann, wenn s''(t) = 0 und s'''(t) < 0 .
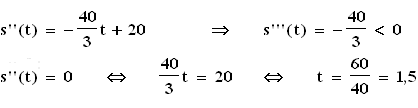 Die Schnecke erreicht ihre größte Geschwindigkeit nach 1,5 Minuten.
Diese Geschwindigkeit beträgt s'(1,5) = 15 cm / min .
3.1
Die Schnecke erreicht ihre größte Geschwindigkeit nach 1,5 Minuten.
Diese Geschwindigkeit beträgt s'(1,5) = 15 cm / min .
3.1 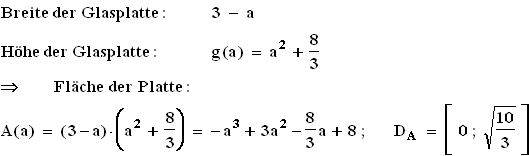 3.2
3.2 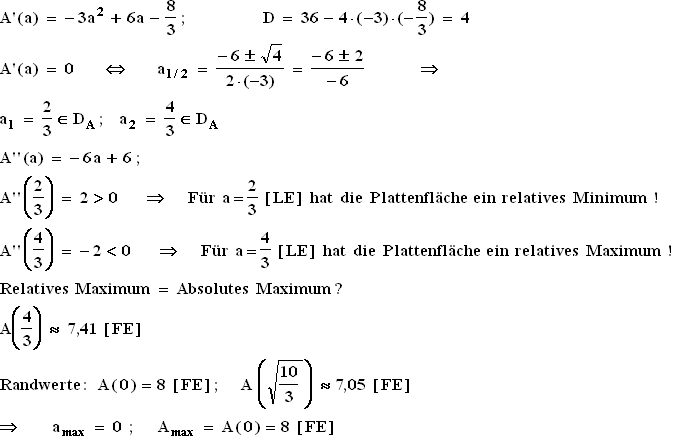
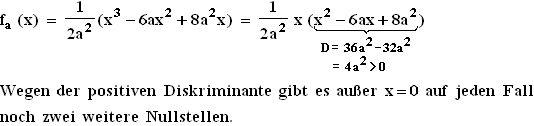
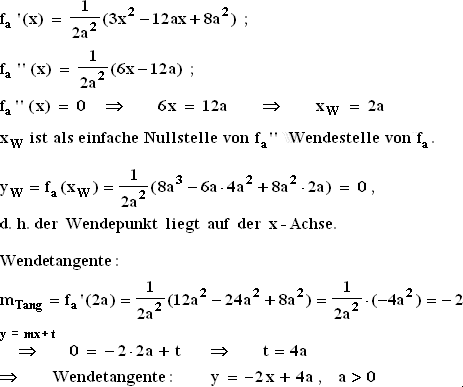
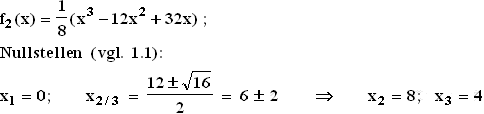
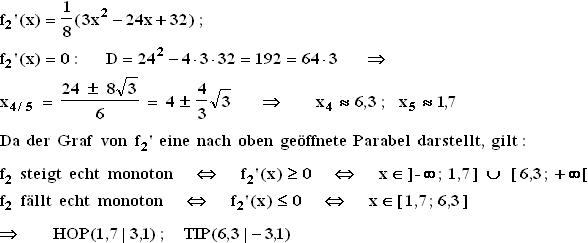 1.3.3 Graf von f2 mit seiner Wendetangente und Graf von p :
1.3.3 Graf von f2 mit seiner Wendetangente und Graf von p :

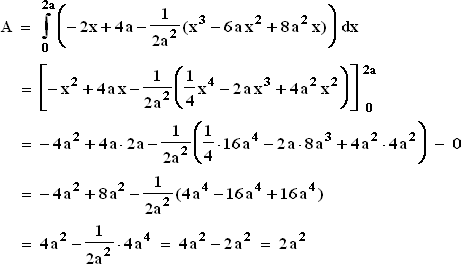
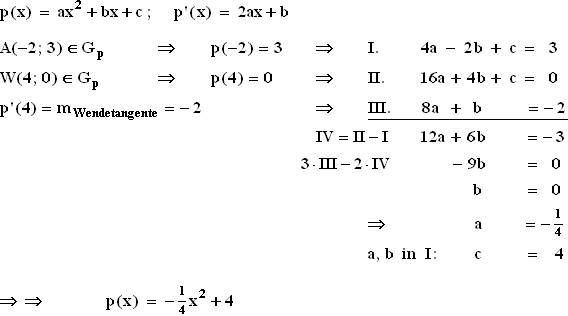
 3.1 28 = 14 + 7 + 4 + 2 + 1
3.1 28 = 14 + 7 + 4 + 2 + 1