Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2004
Aufgabengruppe A: A I A II
A I
1.0
Gegeben sind die reellen Funktionen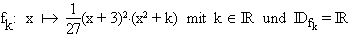 
.
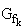bezeichnet.
1.1
Es sei zunächst k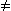 
–9. Ermitteln Sie in Abhängigkeit von k die Lage der Nullstellen sowie deren Vielfachheit. Unterscheiden Sie dabei die Fälle k > 0, k = 0 und k < 0. (7 BE)
Für alle folgenden Teilaufgaben ist k = –9 und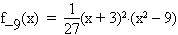 
.
1.2
Zeigen Sie, dass f–9 eine einfache und eine dreifache Nullstelle besitzt. Geben Sie jeweils auch die Lage dieser Nullstellen an. (3 BE)
1.3
Der zur Funktion f–9 gehörende Funktionsterm lässt sich auch in folgender Form darstellen:
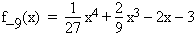(Nachweis nicht erforderlich!)
1.3.1
Ermitteln Sie die x-Koordinaten aller Punkte, in denen der Graph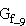 
waagrechte Tangenten besitzt. (6 BE)
1.3.2
Bestimmen Sie die maximalen Intervalle, in denen der Graph 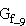rechts- bzw. linksgekrümmt ist und die Koordinaten der Wendepunkte. Ermitteln Sie dann die Gleichung derjenigen Wendetangente an den Funktionsgraphen, die nicht waagrecht verläuft. (9 BE)
1.3.3
Zeichnen Sie den Graphen 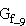für 
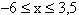mit Hilfe einer geeigneten Wertetabelle in ein kartesisches Koordinatensystem.
Maßstab auf beiden Achsen: 1 LE = 1 cm. (6 BE)
1.3.4
Kennzeichnen Sie farbig in der Zeichnung von 1.3.3 die folgende Punktmenge:
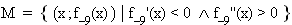(3 BE)
1.3.5
Die Gerade t mit der Gleichung y = –2x – 3 und der Graph 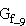schließen ein im II. und III. Quadranten liegendes Flächenstück ein. Zeichnen Sie die Gerade t in das Koordinatensystem von 1.3.3 ein und berechnen Sie die Maßzahl des Flächeninhalts. (7 BE)
1.4
Gegeben ist nun die abschnittsweise definierte Funktion
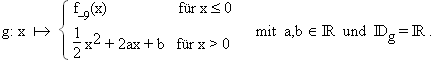
Ermitteln Sie a und b so, dass die Funktion g an der Stelle x0 = 0 stetig und differenzierbar ist. (7 BE)
2.0
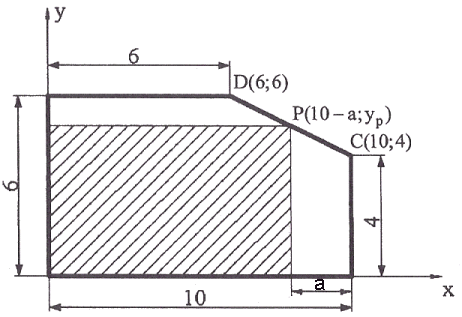
Aus einem fünfeckigen Brett soll ein rechteckiges Stück herausgesägt werden (siehe Skizze unten). Dabei soll der Punkt P auf der Strecke [CD] liegen.
2.1
Stellen Sie die Flächenmaßzahl A(a) des Rechtecks in Abhängigkeit von der Streckenlänge a dar und geben Sie eine sinnvolle Definitionsmenge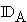 
der Funktion A an.
( Mögliches Teilergebnis: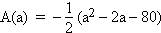 
) (6 BE)
2.2
Berechnen Sie nun denjenigen Wert von a, für den die Rechtecksfläche den größten Wert annimmt. Berechnen Sie auch, wie groß in diesem Fall der „Abfall“ in Prozent bezogen auf die Fläche des Fünfecks ist. (6 BE)
A II
1.0
Gegeben sind die Funktionen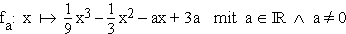 
in der Definitionsmenge 
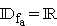. Der Graph einer solchen Funktion wird mit 
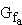bezeichnet.
1.1
Zeigen Sie, dass die x-Koordinate des Wendepunkts des Graphen 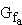von a unabhängig ist. (3 BE)
1.2
Weisen Sie nach, dass sich der Funktionsterm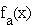 
auch in der Form 
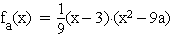schreiben lässt und bestimmen Sie Anzahl und Lage der Nullstellen der Funktion 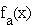in Abhängigkeit von a.
Hinweis: Führen Sie eine geeignete Fallunterscheidung durch. (8 BE)
Für alle folgenden Teilaufgaben ist a = 1 und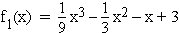 
.
1.3
Berechnen
Sie die Art und die Koordinaten der Extrempunkte sowie die Koordinaten des Wendepunkts des Graphen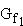 
. (7 BE)
1.4
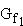Zeichnen Sie unter Verwendung der bisherigen Ergebnisse und geeigneter Funktionswerte den Graphen für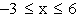 
in ein Koordinatensystem.
Maßstab auf beiden Achsen: 1 LE = 1 cm. (6 BE)
1.5
Berechnen Sie die x-Koordinaten der Schnittpunkte der Graphen 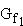und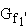 
(Ableitung). Runden Sie gegebenenfalls auf 2 Nachkommastellen.
(Teilergebnis: Die ganzzahlige Lösung ist x = 3. ) (7 BE)
1.6
Der Graph 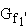der Funktion 
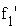ist eine Parabel.
Berechnen Sie die Koordinaten ihres Scheitels. Zeichnen Sie den Graphen 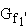für 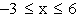in das vorhandene Koordinatensystem. (5 BE)
1.7
Beschreiben Sie den Zusammenhang zwischen der Wendetangente von 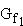und der y-Koordinate des Scheitels von 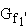in Worten. (2 BE)
1.8
Berechnen Sie die Maßzahl des Flächenstücks, das die Graphen 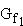und 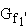sowie die y-Achse im I. und IV. Quadranten einschließen. (5 BE)
2.0
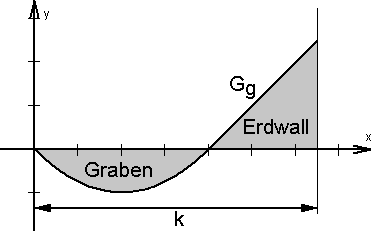
Die nebenstehende Skizze
zeigt den Querschnitt durch
einen ausgehobenen Graben
und einen aufgeschütteten
Erdwall.
Der Graph Gg ist der Graph
der abschnittsweise definier-
ten Funktion
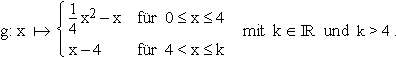
2.1
Zeigen Sie rechnerisch, dass der Übergang vom Graben zum Erdwall stetig und „ohne Knick“ verläuft. (6 BE)
2.2
Stellen Sie die Maßzahl der Querschnittsfläche A(k) des Erdwalls in Abhängigkeit von k dar. (3 BE)
2.3
Der Aushub, der bei der Erstellung des Grabens anfällt, soll vollständig als Erdwall verwendet werden. Bestimmen Sie k so, dass die Querschnittsfläche des Erdwalls genau so groß ist wie die Querschnittsfläche des Grabens. (8 BE)