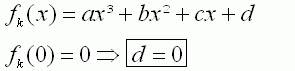
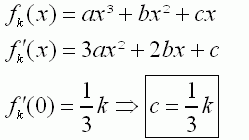
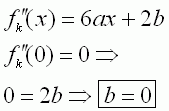
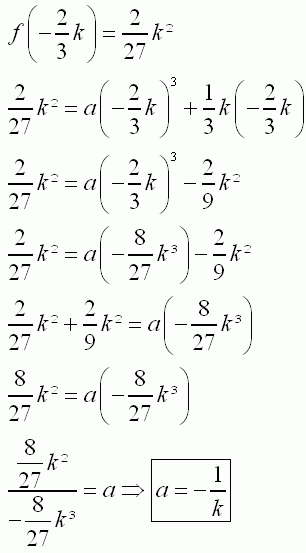
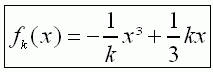
| 1.1 | ||
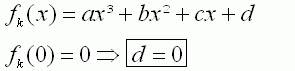 |
||
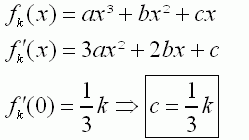 |
||
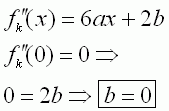 |
||
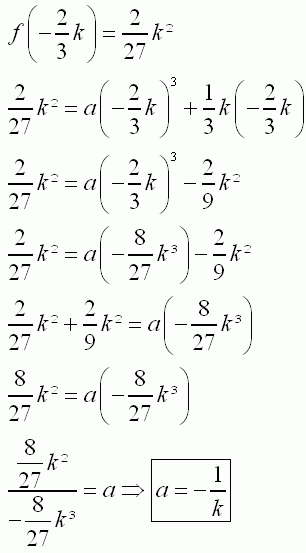 |
||
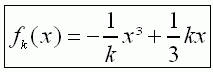 |
| 1.2 | ||||||
|
| 1.3 | ||
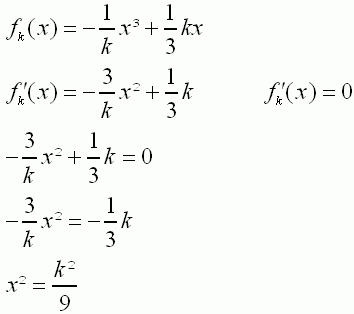 |
||
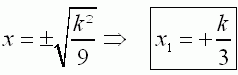 |
||
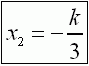 |
||
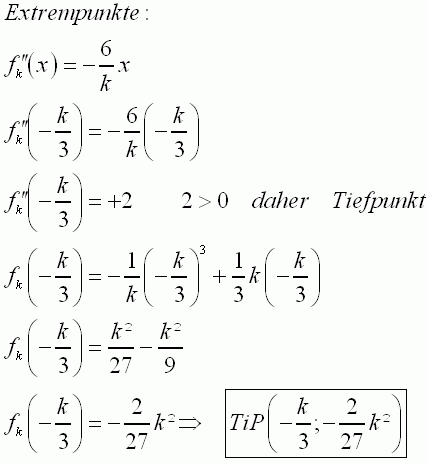 |
||
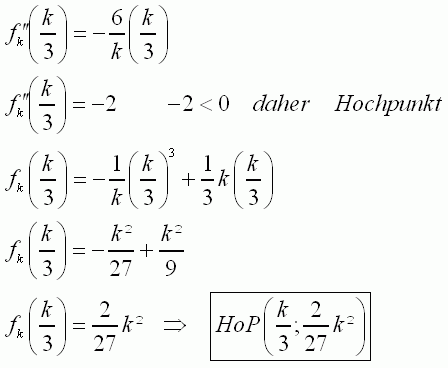 |
||
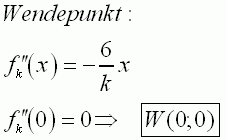 |
||
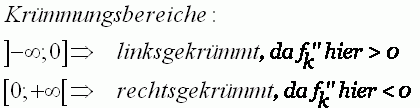 |
| 1.4 | ||
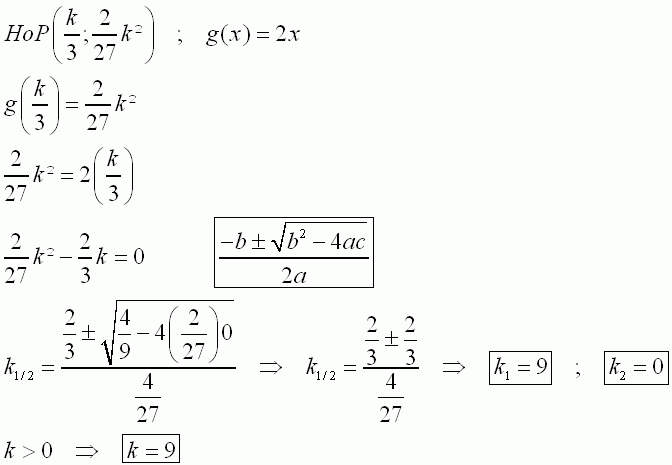 |
| 1.5 | ||
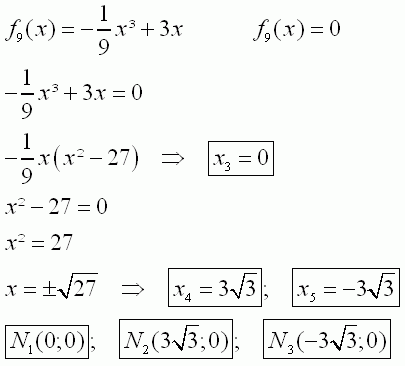 |
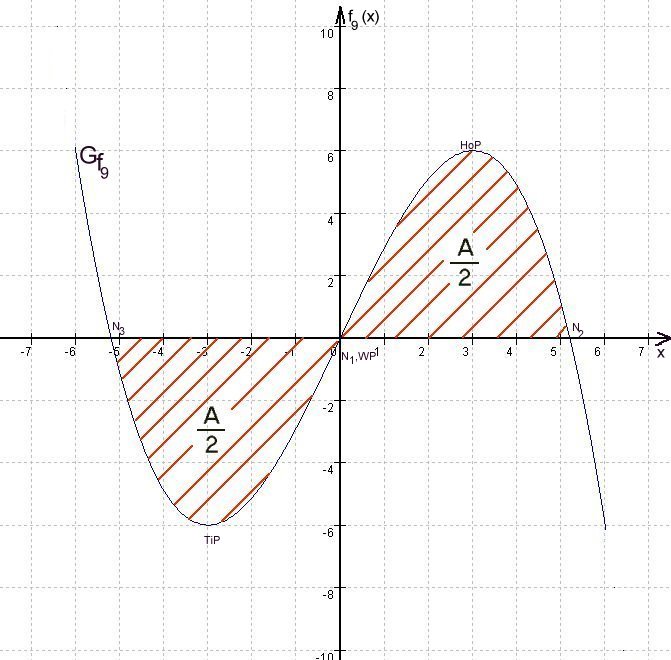
| 1.6 | ||
 |
||
 |
| 2.1 | ||
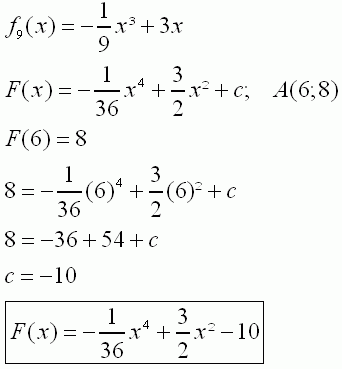 |
| 2.2 | Die maximalen Intervalle bei denen die Funktion F echt monoton zunimmt: | |
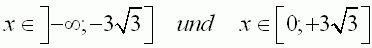 Begründung: F' = f9 ist in diesen Intervallen positiv. |
||
| Die maximalen Intervalle bei denen die Funktion F echt monoton abnimmt: | ||
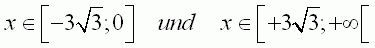 Begründung: F' = f9 ist in diesen Intervallen negativ. |
| 2.3 | ||
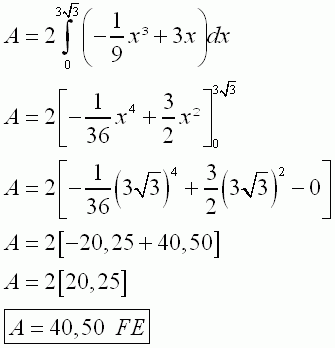 |
| 3.1 | ||
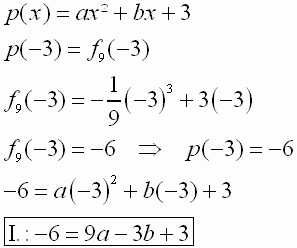 |
||
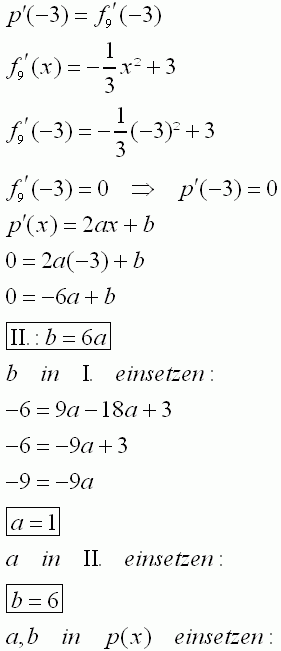 |
||
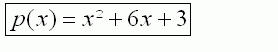 |
| 3.2 | ||||||||
|
||||||||
|
| 4.1 | ||
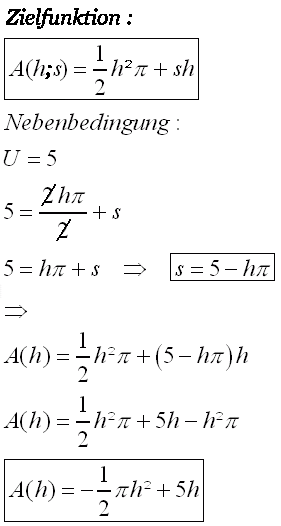 |
||
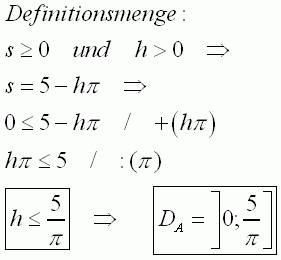 |
| 4.2 | ||
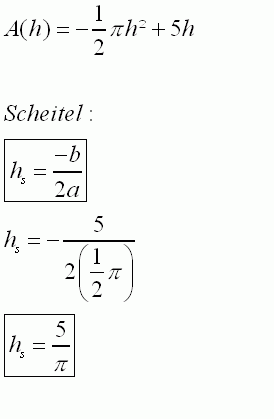 Für dieses hs wird die Querschnittsfläche maximal, da der Graph von A eine nach unten geöffnete Parabel ist, und somit der Scheitel deren höchsten Punkt darstellt. 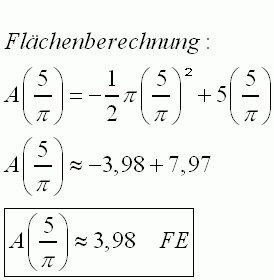 Wenn die Querschnittsfläche diesen Wert annimmt, dann hat sie die Form einer halben Kreisscheibe, denn s ist in diesem Fall Null. |
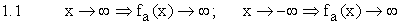 |
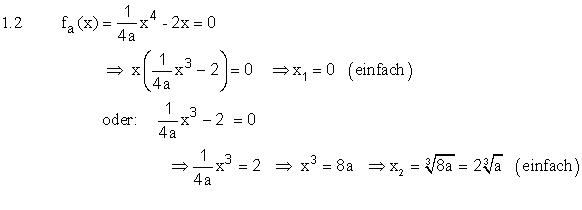 |
 |
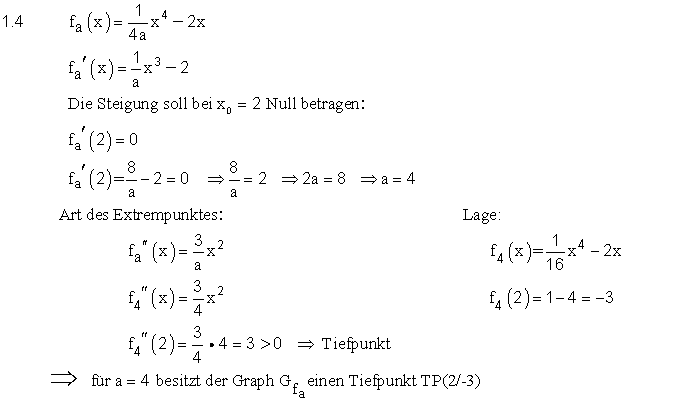 |
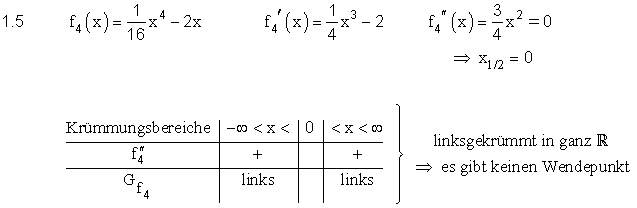 |
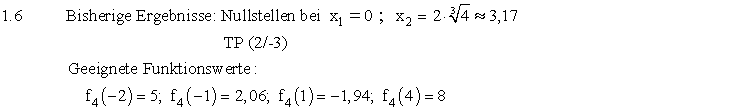 |
 |
 |
1.8.1
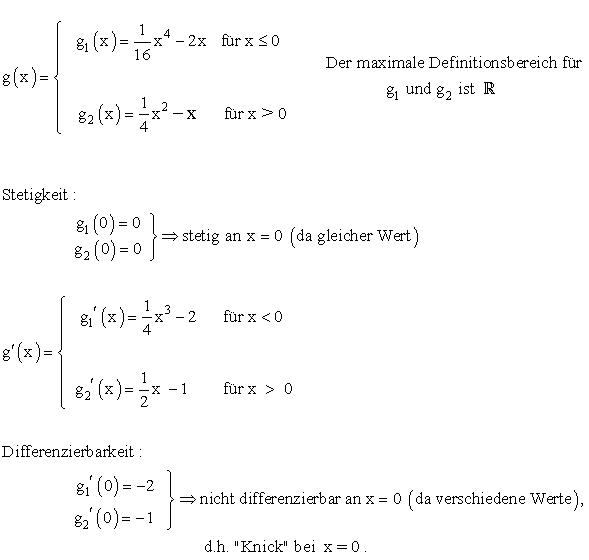 |
1.8.2
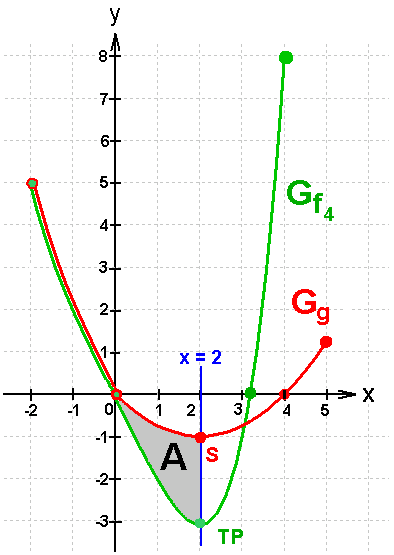 |
1.9
Flächenstück siehe 1.8.2
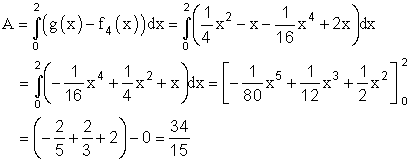 |
 |
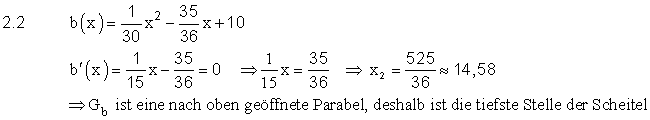 |
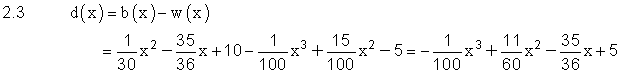 |
 |