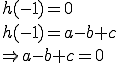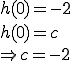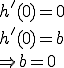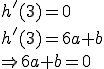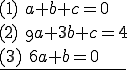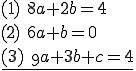Aufgabengruppe A
A II (Lösungen)

 

1.1

Somit gilt in . Damit ist der Graph von f achsensymmetrisch zur y-Achse.

1.2

(Beide sind doppelte Nullstellen: Faktorisierung [(x+2)(x-2)]² )

1.3
Der Graph von g ist aus dem Graphen von f durch Verschiebung um 3 LE nach oben entstanden. Für den Graphen von f sind die beiden doppelten Nullstellen jeweils relative Maximalstellen. Der Graph von g hat demnach zwei Hochpunkte (da er wegen a = -0,25 nach unten offen ist):


Aufgrund der Symmetrie von (und damit auch von ) muss zwischen den beiden Hochpunken bei x = 0 ein Tiefpunkt liegen, also .

Alternativ mit Ableitung - Anmerkung: das entspricht aber nicht der Aufgabenstellung und führt zu Punktabzug:





und
Die Ableitung wird aber für 1.4 benötigt.

1.4

1.5






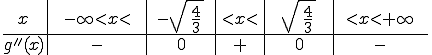
ist rechtsgekrümmt in , sowie in . ist linksgekrümmt in .


(auch wegen Symmetrie!)

1.6








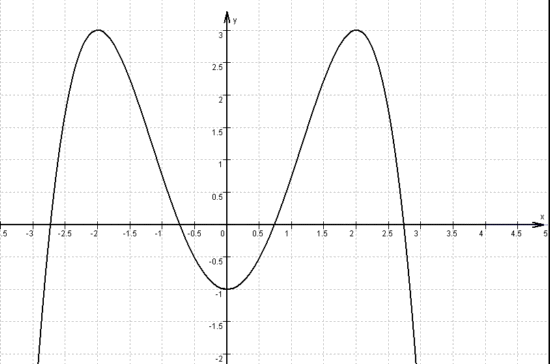
1.7



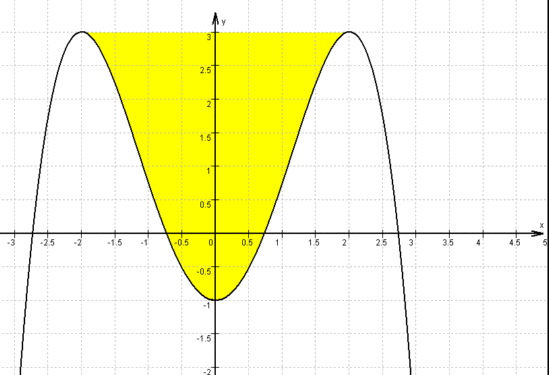
Die Strecke ist Teil der Geraden y = 3
Fläche zwischen zwei Graphen, d.h. Differenz der Funktionsterme integrieren.
3 - g(x)




2.

2.1

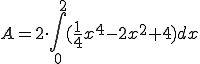
2.3
(A): Der Graph verläuft oberhalb der x-Achse.
(B): Der Graph hat nur negative Tangentensteigungen (er ist echt monoton fallend).
(C): Der Graph ist in diesem Intervall linksgekrümmt.

2.4
a) , und (Die Schreibweise ist auch möglich, wichtig ist, dass 6 ausgenommen wird.)
b)

2.5

1. Term: ; (1) (2) (3) Zwischenergebnis: b und c in (1):

Schneller ist folgende Methode: Nullstellen +1 und -1, also ist h(x) = a(x2 - 1) Scheitel S(0/-2) a = -2

2. Term: ; (1) 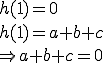(2) 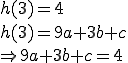(3) in (2) : in (3):

Schneller ist folgende Methode: Scheitel S(3/4) h(x) = a(x - 3)2 + 4 Nullstelle x = 1 0 = a(1 - 3)2 + 4 0 = 4a + 4 also a = -1

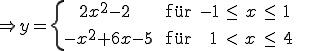
3.1



An den Stellen und weist der Graph deutliche "Knickstellen" auf. Demnach ist die Funktion an diesen Stellen
nicht differenzierbar .

3.2



;

3.3

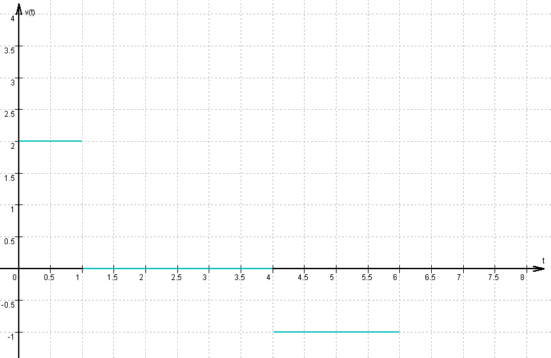
3.4


; ;

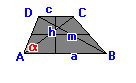
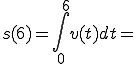"Fläche unter dem Graphen"

 

Seminararbeit

Melanie Rothkegel