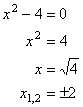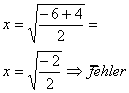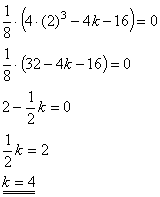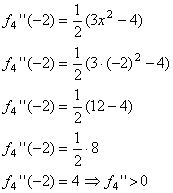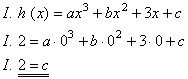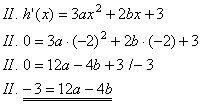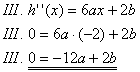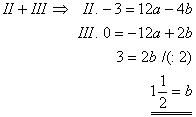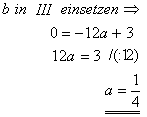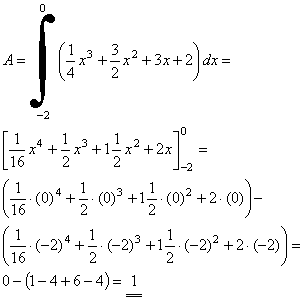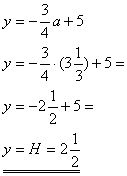Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2007

A I:   Lösungen
 

1.1
Für k > 0 ist x = 0 einfache und x = k doppelte Nullstelle,
für k = 0 ist x = 0 dreifache Nullstelle.
1.2

Der Graph ist linksgekrümmt in und rechtsgekrümmt in .


oder einfacher mit dem faktorisierten Term:
,
also hat der Graph den Wendepunkt .
1.3 Steigung der Tangente:

Steigung und Koordinaten von W in die allgemeine Geradengleichung y = mx + t eingesetzt:

Wir erhalten die Tangentengleichung
1.4 Die Höhe des Dreiecks ist .
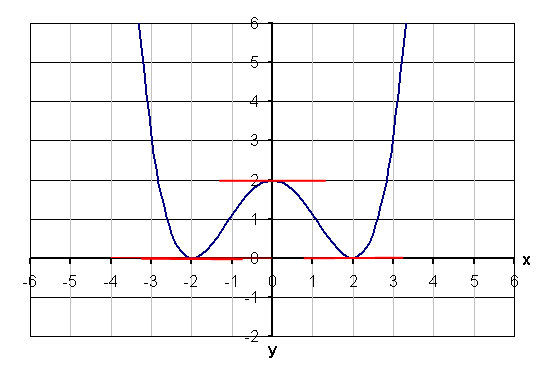
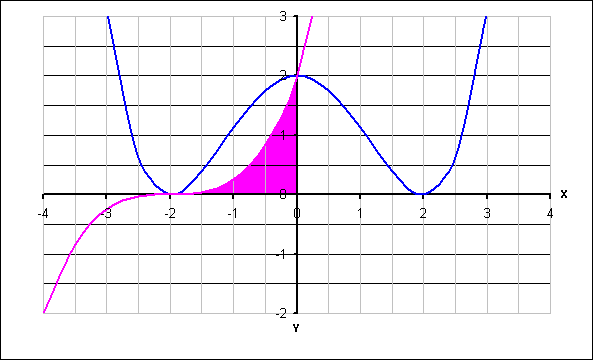
Die Grundlinie wird durch die Nullstelle bestimmt:
, also und damit

[k = -9 scheidet wegen k > 0 als Lösung aus]
2.1
mit
Da der Graph des Terms eine nach oben offene Parabel darstellt, folgt:
die Ableitung ist positiv für x < 1 und x > 3, bzw. negativ für 1 < x < 3 ,
also ist der Graph streng monoton wachsend in sowie in und
streng monoton fallend in [1 ; 3].
Auf Grund des Vorzeichenwechsels in der Steigung von + nach - bzw. von - nach +
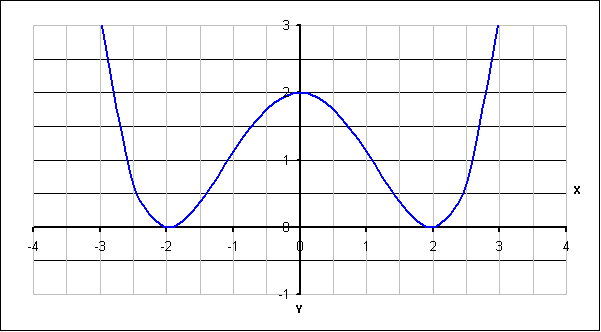
erhalten wir den Hochpunkt H(1/1,33) bzw. den Tiefpunkt T(3/0).
2.2
Wendepunkt und Wendetangente für k = 3: 		f(-0,5) = -2,04
f(4) = 1,33
2.3
Die Fläche besteht aus zwei Teilen: bis x = 2 ist es die Fläche unter der Kurve, ab x = 2 die Fläche unter der Tangente.
3.1


Der Graph geht durch den Ursprung, also ist d = 0.

Man erhält folgendes Gleichungssystem:


      

Durch Einsetzen erhält man
und
und damit

3.2
Die Terme der einzelnen Abschnitte haben für sich betrachtet den maximalen Definitionsbereich IR, also kann auf die Grenzwertdarstellung verzichtet werden. Es gilt

und .
Das bedeutet, g(x) ist an den betrachteten Stellen differenzierbar, da es nach Voraussetzung schon stetig ist.
3.3 Dies ist im Wendepunkt (=Extrempunkt der Steigung) der Fall:


W(-3/1,44) ist ein Wendepunkt, da x = -3 eine einfache Nullstelle von g'' ist (Vorzeichenwechsel der Krümmung).

 

 

 

A II:   Lösungen
 

1.1
. Dadurch dass die Variable k stets kleiner als "0" (k<0) sein soll, kann der Faktors (x²-k) niemals "0" werden, und in ihm somit keine Nullstelle enthalten sein . Siehe Beispiel:
 
Wir setzen für k eine Zahl kleiner als "0" ein, k= -2. In der zweiten Zeile ist schon der erste Fehler sichtbar, eine 2er Potenz kann niemals eine negative Zahl ergeben.  
         
 

Somit müssen die beiden Nullstellen im zweiten Faktor (x²-4) enthalten sein. Um die Nullstellen zu finden, können wir den Faktor einfach nullsetzen und auflösen. Die Nullstellen sind somit = +2 und = -2. Da beide Nullstellen einfache Nullstellen sind, sind es keine Berührstellen sondern Schnittpunkte mit der x-Achse.

 

1.2 Enthält ein Term nur gerade Exponenten, so ist der Graph achsensymmetrisch zur y-Achse. Dieser Umstand ist in diesem Falle gegeben.  
 

 

1.3
Eine waagrechte Tangente bedeutet, dass eine waagrechte Gerade den Graphen berührt. Siehe Beispiel:  
 
 
     
 
Eine waagrechte Tangente kann nur an den Hoch- bzw. Tiefpunkten sowie evtl. Terrassenpunkten des Graphen existieren. An diesen Punkten hat ein Graph stets die Steigung null. Somit können wir die Stellen mithilfe der Steigungsfunktion (1. Ableitung der Funktion) berechnen.  
  So lautet die abgeleitete Funktion. Die Ableitung wird = 0 gesetzt:  
         
  Die Gleichung mit vier multiplizieren um das Rechnen zu erleichtern  
         
  x kann ausgeklammert werden, somit gilt =0  
         
 

 

      
         
  Wird für k der Wert -4 oder kleiner gewählt, bleibt es bei der einen Nullstelle =0. ( für k = -4 ist es dann eine dreifache Nullstelle )  
         
    Beispiel mit k=-6. Fehler in der zweiten Zeile, eine 2er Potenz kann niemals eine negative Zahl ergeben. In diesem Fall also nur eine Nullstelle =0. (vergl. auch Aufg. 1.1)  
         
  Wird für k eine Wert größer als -4 eingesetzt gibt es insgesamt drei Nullstellen. (Siehe Lösung).  
         
     

 

1.4
Wenn der Graph der Funktion die x- Achse bei =2 berühren soll, so muss sein, da der Graph an der Stelle x=2 einen Extrempunkt braucht, und es muss sein (siehe 1.1). Jetzt kann man in die abgeleitete Funktion für x den Wert 2 einsetzen um k zu erhalten.  
 
 
Ergebnis: k=4

 

 

 

2.1  Die Nullstellen können wie folgt ausgerechnet werden.  
 

Aus der Klammer können wie gezeigt zwei Nullstellen errechnet werden. Da der Faktor bzw. die Klammer doppelt vorhanden ist, ist jede Nullstelle eine doppelte Nullstelle.

Somit erhalten wir für und für

 

Ergebnis: ;

 

2.2 Die Extrempunkte sind die Hoch- und Tiefpunkte eines Graphen. Eine Bedingung für Hoch- oder Tiefpunkt ist, dass die erste Ableitung der Funktion den Wert "0" ergibt. Also leiten wir die Funktion einmal ab.  
    Funktionsgleichung.  
    Die Funktion wird einmal abgeleitet.  
    Die Vier kann ausgeklammert werden, um das Rechnen zu erleichtern.  
    x kann ausgeklammert werden, das bedeutet besitzt den Wert "0".  
    Die Ableitung wird = 0 gesetzt, die Gleichung umgestellt, um sie nach x aufzulösen.  
         
    hat den Wert +2 und den Wert -2.  
           
 

 

 

Jetzt setzen wir die gefundenen x-Werte in die Funktion ein, um die ensprechenden y-Werte zu errechnen. Beispiel mit Wert "0". Für x=0 erhalten wir somit .

Werte für x= : ; .

 
           
 

 

 

Beispiel mit

Ob es sich bei den errechneten Extremwerten um Hoch- oder Tiefpunkte handelt, lässt sich wie folgt errechnen. Ist handelt es sich um einen relativen Hochpunkt, ist handelt es sich um einen relativen Tiefpunkt.

kleiner als "0", also Hochpunkt.

größer als "0" also Tiefpunkt.

größer als "0" also Tiefpunkt.

 
           
Bedingung für einen Wendepunkt ist, dass die zweifach abgeleitete Funktion den Wert "0" ergibt.  
    Zweifach abgeleitete Funktion.  
    Die 2. Ableitung der Funktion soll "0" ergeben.  
    Gleichung umstellen um nach x aufzulösen, und durch teilen.  
    und erhält man, wenn man die Wurzel aus vier drittel zieht.  
   
Es sind einfache Nullstellen von f '' mit Krümmungswechsel, also Wendepunkte.  
           
   

Die errechneten Werte für und in die Funktionsgleichung einsetzen um die entsprechenden y-Werte zu erhalten. Da für die x-Werte nur gerade Exponenten vorhanden sind, erhalten wir für jeweils . Die Wendepunkte errechnen sich zu und.

 

  
       

Ergebnisse:

Koordinaten der Extrempunkte: ; : ; .

Extrempunkt Hoch- oder Tiefpunkt.

ist kleiner als "0", also Hochpunkt.

ist größer als "0" also Tiefpunkt

ist größer als "0" also Tiefpunkt.

Wendepunkte:

; .

 

2.3
Randwerte: f(3) = 3,125 = f(-3)
 
 
     

 

 

 

3.1

 

 

Zunächst leitet man sich die gegeben Funktion zweimal ab, da die erste und zweite Ableitung zum finden der Unbekannten notwendig sind.  
           
    In der Aufgabenstellung ist gegeben, dass der Graph den Graphen von auf der y-Achse schneidet. Aus Aufgabe 2.2 wissen wir, dass an der Stelle x=0 (auf der y-Achse) den y-Wert "2" besitzt. Somit kann man in die Funktion für x=0, und für y=2 einsetzen: h(0) = 2  
           
    Weiter ist gegeben, dass bei x=-2 und y=0 einen Terassenpunkt besitzt. Bei einem Terrassenpunkt sind Steigung und Krümmung Null. Deshalb kann man den x-Werte in die erste und zweite Ableitung einsetzen und erhält somit zwei Gleichungen für das Gleichungssystem. Hier h'(-2) = 0:  
           
    Und hier h''(-2) = 0:  
           
 

 

 

 

 

Unsere Gleichungen zur Lösung der Gleichungssystems.  
           
    Durch Addition von Gleichung II und III erhält man die Variable b.  
           
    Setzt man b in Gleichung III ein, so erhält man a.  
           
    Jetzt können wir die Ergebnisse a= , b= und c= 2 für die Variablen einsetzen, und erhalten unsere Funktion .  
       
Ergebnisse: ; ; ;

 

3.2 Bewiesen werden soll, dass sich die Graphen und bei berühren, und bei schneiden, aber nicht berühren.  
 

 

 

Bei Einsetzen des selben x-Wertes (x=-2) in die Funktionen und erhält man die selben y-Werte (y=0). Somit ist bewiesen, dass beide Graphen einen gemeinsamen Punkt bei haben. Setzt man denselben x-Wert (x=-2) in die ersten Ableitungen von und ein, errechnen sich ebenfalls die selben Steigungswerte (y'=0). Somit ist bewiesen, dass die beiden Funktionen an der selben Stelle die selbe Steigung "0" besitzen und sich somit berühren.  
           
 

 

 

Beim Einsetzen des selben x-Wertes (x=0) in die Funktionen von und erhält man die selben y-Werte (y=2). Somit ist bewiesen, dass beide Graphen noch einen gemeinsamen Punkt haben. Setzt man denselben x-Wert (x=0) in die ersten Ableitungen von und ein, errechnen sich nicht dieselben Steigungswerte. Für errechnet sich "2", und für errechnet sich "3". Sie besitzen an der selben Stelle somit nicht die selbe Steigung, und müssen sich deshalb schneiden.

 

3.3 Die Graphen der Funktionen und .  
Randwerte von h: h(-4) = -2 , h(1) = 6,75
 
 
 
   

 

3.4 Die pink eingefärbte Fläche soll berechnet werden.  
 
 
     
    Zuerst muss der Funktionsterm des entsprechenden Graphen "aufgeleitet" werden.  
           
   

Um das Integral der Funktion im Bereich [-2/0] zu berechnen, muss die Funktion aufgeleitet werden, aus der Funktion "h" wird somit die Stammfunktion "H" bestimmt .

 

 

Die Grenzen -2 und 0 werden eingesetzt:
H(0) - H(-2)

 

 

Ergebnis:

 

 

 

4.1 Die Fläche des Fensters lässt sich durch die Formel berechnen. Als Breite (B) können wir erkennen, dass ist. Man kann erkennen, dass die beiden Dachschrägen jeweils eine lineare Funktion () darstellen, mithilfe derer man den y-Wert und somit die Höhe (H) des Fensters berechnen kann.  
    Wir können erkennen, dass die Graphen auf acht Längeneinheiten auf der x-Achse sechs Längeneinheiten auf der y-Achse steigen, bzw. fallen. Also haben wir für die Steigung bzw. . Außerdem kann man ablesen, dass die Graphen die y-Achse bei y=6 schneiden. Also haben wir für t=6. So lässt sich die Funktionsgleichung für den Graphen aufstellen.  
           
    Somit können wir den y-Wert der eben errechneten linearen Funktion für die Höhe (H) in Formel einsetzen. Allerdings muss noch der Wert eins abgezogen werden, da das Fenster 1 LE über der x- Achse beginnt.  
           
Zur Angabe der Definitionsmenge: “a” kann zwischen min.=0 und höchstens bis zum Beginn der Dachschräge gewählt werden. So hat das Fenster bei a=0 die maximale Höhe, und bei “a” bis Ende der Dachschräge die maximale Breite. Es gilt nun dieses "a" max. rauszufinden um die Definitionsmenge angeben zu können.  
   
     
   

Wir wissen, dass sich das Fenster auf der Höhe 1 LE befindet, somit können wir für y=1 einsetzten. Dann die Funktion einfach nach a auflösen, und wir erhalten den maximalen Wert für "a". Die Definitionsmenge liegt somit zwischen "0" und ..

 

 

 

 
       
Ergebnisse: ;

 

4.2  
   

Der Wert für a, bei dem die Fläche des Fensters den größten Wert erreicht, erhält man, indem man die Funktion einmal ableitet, null setzt und nach a auflöst.

Der Term wird graphisch durch eine nach unten offene Parabel beschrieben, deren Extrempunkt ist ein Hochpunkt. Das heißt, die Fläche wird an dieser Stelle maximal.

 
           
    Die Breite des Fensters beträgt .  
           
   

Der gefundene Wert für a kann jetzt in die lineare Funktion eingesetzt werden. Bei der Funktion wurde eine LE abgezogen, da sich das Fenster eine LE über der x- Achse befindet. Man erhält den Wert für y bzw. H. Die Höhe des Fensters beträgt .

Ergebnisse: , ; .

 

  Exponent Ist die Hochzahl einer Potenz; der Exponent gibt an, wie oft die Basis (Grundzahl) mit sich selbst multipliziert werden soll; z. B. 43 = 4 · 4 · 4.  
  Variable Ist eine veränderliche Größe (einer Funktion, einer definierbaren Menge) z.B."x" oder "k". Für sie können verschiedene Zahlen eingesetzt werden.  
  Faktor Zahl, die mit einer anderen multipliziert wird, Multiplikand, Multiplikator. Bestandteil eines Produkts .