Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2008
A I : Lösungen
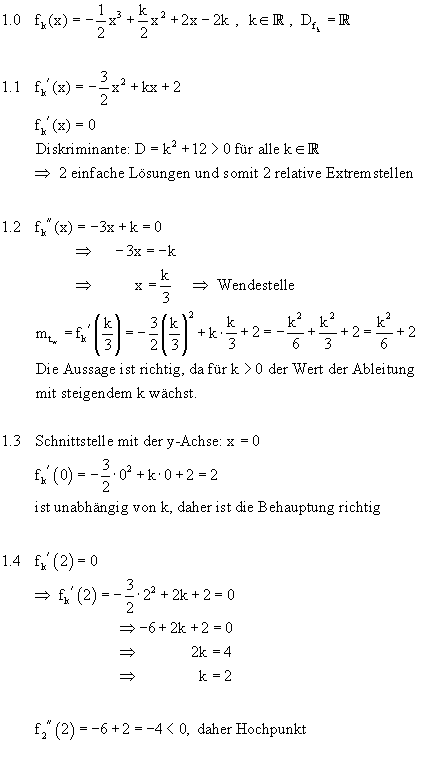
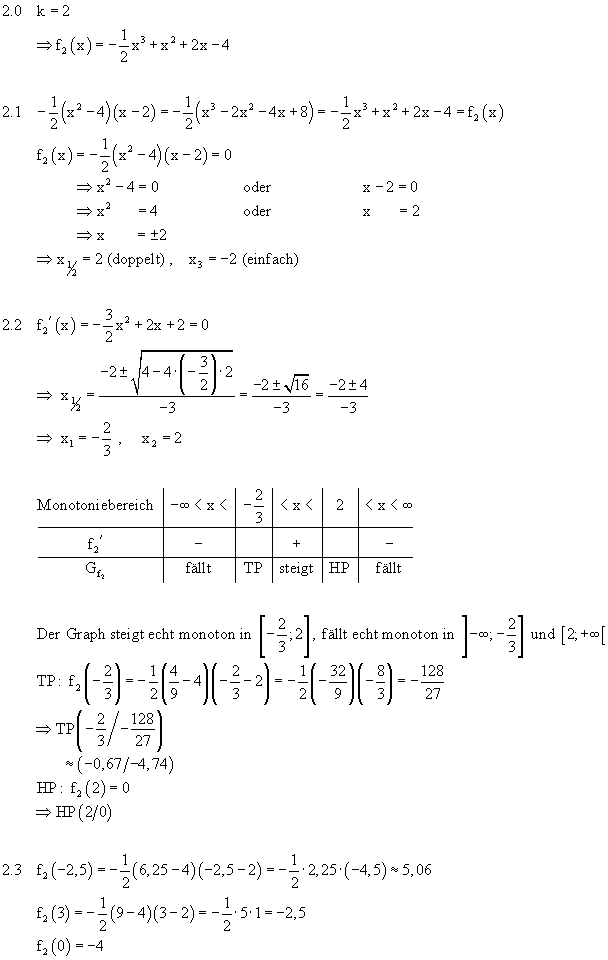

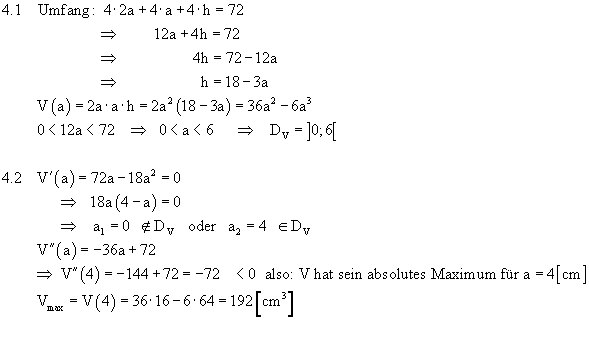
| Lösungen zur Prüfung zur Erlangung der Fachhochschulreife Aufgabengruppe AII Frühjahr 2008 |
||
| Seminararbeit Sarah Rabura Oktober 2008 Korrigiert von OStR Peter Starfinger |
||
1.1 |
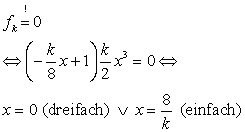
Die Vorraussetzungen f(x) = f(-x) (für Achsensymmetrie) f(x) = -f(-x) (für Punktsymmetrie) sind nicht erfüllt, also ist der Graph asymmetrisch. |
|
1.2 |
|
|
2.1 |
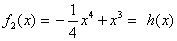
Für 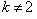 (Angabe): (Angabe):
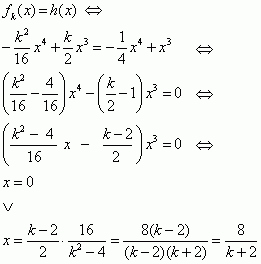
| |
2.2 |
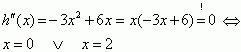
einfache Nullstellen von h'', also Wendestellen von h. Koordinaten der Wendepunkte: WEP1 (0/0) WEP2 (2/4) Da x = 0 eine doppelte Horizontalstelle von h ist, muss WEP1 ein Terrassenpunkt sein (vgl. Aufgabe 1.2). |
|
2.3 |
Nullstellen von 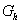 (siehe auch 1.1): (siehe auch 1.1):
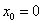 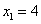
Hochpunkt (siehe auch 1.2): 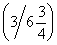
Somit ergibt sich nach Berechnung weiterer Funktionswerte der Graph: 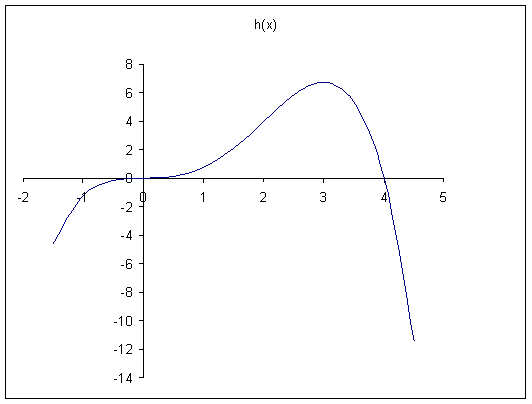
| |
2.4 |
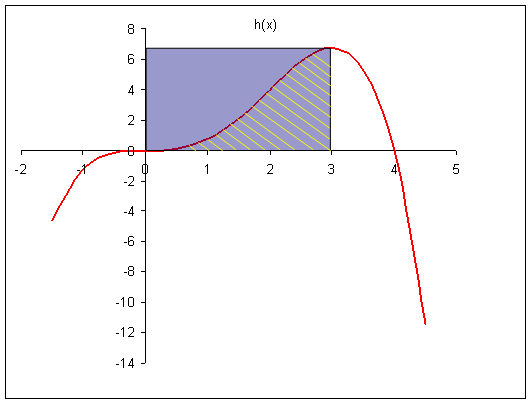
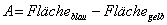
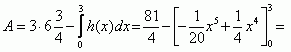
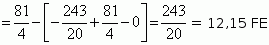
| |
3.0 |
|
|
4.1 |
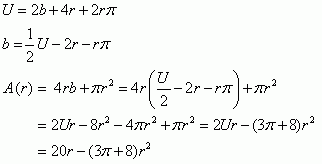
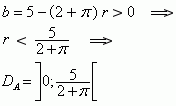 |
|
4.2 |

Da der Graph von A eine nach unten ge÷ffnete Parabel ist und somit ihr Extremum ein Maximum darstellt, wird für r = 0,574 die Fensterfläche maximal. 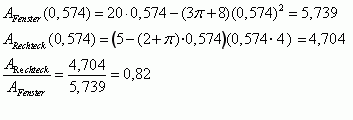
Das Rechteck nimmt etwa 82% der Fensterfläche ein. |
|