Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 1999
A I: Lösungen
1.1.1 f ''(x) = –3x2 + 6ax  f '(x) = –x3 + 3ax2 + b
f '(x) = –x3 + 3ax2 + b  f(x) = –0,25x4 + ax3 + bx + c
WEP bei x = 2
f(x) = –0,25x4 + ax3 + bx + c
WEP bei x = 2  f ''(2) = 0
f ''(2) = 0  –12 + 12a = 0
–12 + 12a = 0  a = 1
f '(0) = –4
a = 1
f '(0) = –4  b = –4
P(2 | 0)
b = –4
P(2 | 0)  f(2) = 0
f(2) = 0  –0,25·16 + 1·8 –4·2 + c = 0
–0,25·16 + 1·8 –4·2 + c = 0  c = 4
c = 4
 f (x) = –0,25x4 + x3 – 4x + 4
1.1.2 f ''(x) = –3x2 + 6x (siehe 1.1.1);
f ''(x) = 0
f (x) = –0,25x4 + x3 – 4x + 4
1.1.2 f ''(x) = –3x2 + 6x (siehe 1.1.1);
f ''(x) = 0  –3x(x – 2) = 0
–3x(x – 2) = 0  x1 = 0
x1 = 0  x2 = 2
x1 und x2 sind Wendestellen von f, da sie einfache Nullstellen von f '' sind.
Art der Wendestellen:
Der Graf von f '' ist eine nach unten geöffnete Parabel, die bei x1 = 0 ihr Vor-
zeichen von – nach + und bei x2 = 2 ihr Vorzeichen von + nach – wechselt.
x2 = 2
x1 und x2 sind Wendestellen von f, da sie einfache Nullstellen von f '' sind.
Art der Wendestellen:
Der Graf von f '' ist eine nach unten geöffnete Parabel, die bei x1 = 0 ihr Vor-
zeichen von – nach + und bei x2 = 2 ihr Vorzeichen von + nach – wechselt.
 Bei x1 = 0 liegt ein Rechts-Links-Krümmungswechsel und bei x2 = 2
ein Links-Rechts-Krümmungswechsel vor.
f (0) = 4
Bei x1 = 0 liegt ein Rechts-Links-Krümmungswechsel und bei x2 = 2
ein Links-Rechts-Krümmungswechsel vor.
f (0) = 4  WEP1(0 | 4)
Schon bekannt: WEP2(2 | 0)
1.1.3 f '(x) = –x3 + 3x2 – 4 (siehe 1.1.1)
Durch Probieren findet man die Nullstelle x3 = 2 von f '.
Eventuelle weitere Nullstellen ermittelt man durch Division von f '(x) durch (x – 2):
WEP1(0 | 4)
Schon bekannt: WEP2(2 | 0)
1.1.3 f '(x) = –x3 + 3x2 – 4 (siehe 1.1.1)
Durch Probieren findet man die Nullstelle x3 = 2 von f '.
Eventuelle weitere Nullstellen ermittelt man durch Division von f '(x) durch (x – 2):
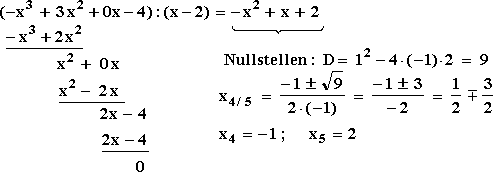 Da x3 = 2 also eine doppelte Nullstelle von f ' ist, muss dort ein Terrassenpunkt
vorliegen.
Monotonieverhalten von f :
Da x3 = 2 also eine doppelte Nullstelle von f ' ist, muss dort ein Terrassenpunkt
vorliegen.
Monotonieverhalten von f :
| | x < | –1 | < x < | 2 | < x |
|---|
| f '(x) | + | 0 | – | 0 | – |
| Graf von f | steigt | HOP | fällt | TEP | fällt |
Wertemenge von f:
f (x) = –0,25x4 + x3 – 4x + 4 ;
f (–1) = 6,75  HOP(–1 | 6,75)
HOP(–1 | 6,75)  Wf = ]–∞ ; 6,75]
1.1.4 f (–2) = 0; f (1) = 0,75; f (3) = –1,25
1.3.1
Wf = ]–∞ ; 6,75]
1.1.4 f (–2) = 0; f (1) = 0,75; f (3) = –1,25
1.3.1 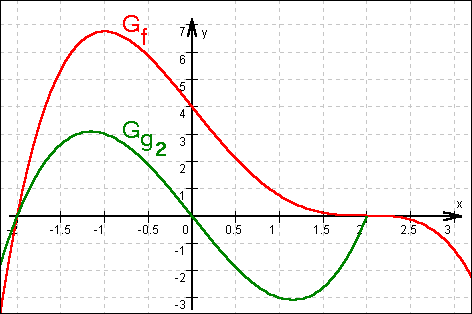 1.2.1 gp(–x) = (–x)3 – p2(–x) = –x3 + p2x = –gp(x)
1.2.1 gp(–x) = (–x)3 – p2(–x) = –x3 + p2x = –gp(x)  Der Graf von gp ist punktsymmetrisch bzgl. O.
Nullstellen von gp:
x
Der Graf von gp ist punktsymmetrisch bzgl. O.
Nullstellen von gp:
x – p
– p x = x (x
x = x (x – p
– p ) = 0
) = 0  x
x = 0
= 0  x
x = p
= p
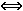 x
x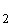

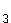 = ± p
Für p ≠ 0 besitzt gp also drei verschiedene einfache Nullstellen,
sonst eine dreifache Nullstelle x1 / 2 / 3 = 0.
1.2.2
= ± p
Für p ≠ 0 besitzt gp also drei verschiedene einfache Nullstellen,
sonst eine dreifache Nullstelle x1 / 2 / 3 = 0.
1.2.2 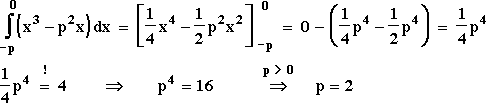 1.3.1 g2(x) = x3 – 4x
1.3.1 g2(x) = x3 – 4x  g2'(x) = 3x2 – 4
g2'(x) = 3x2 – 4  g2''(x) = 6x
g
g2''(x) = 6x
g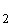 '(x) = 0
'(x) = 0  3x
3x = 4
= 4 
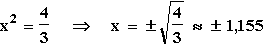 g2''(–1,155) < 0
g2''(–1,155) < 0  HOP(–1,155 | 3,08)
Wegen der Punktsymmetrie des Grafen von g2 bzgl. O muss dann gelten:
TIP(1,155 | –3,08)
1.3.2 Das Integral
HOP(–1,155 | 3,08)
Wegen der Punktsymmetrie des Grafen von g2 bzgl. O muss dann gelten:
TIP(1,155 | –3,08)
1.3.2 Das Integral 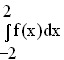 stellt geometrisch den Inhalt der Fläche zwischen G
stellt geometrisch den Inhalt der Fläche zwischen G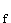 und der x-achse dar.
Diese Fläche unterscheidet sich von derjenigen zwischen den Grafen von f und g2 dadurch,
dass sie für –2 < x < 0 um die Fläche zwischen dem Grafen von g2 und der x-Achse größer
und für 0 < x < 2 wegen der Punktsymmetrie des Grafen von g2 um eben diese Fläche
kleiner ist. Daher sind die beiden betrachteten Flächen gleich groß.
2. Die Summanden heißen x und y. Es gilt also:
und der x-achse dar.
Diese Fläche unterscheidet sich von derjenigen zwischen den Grafen von f und g2 dadurch,
dass sie für –2 < x < 0 um die Fläche zwischen dem Grafen von g2 und der x-Achse größer
und für 0 < x < 2 wegen der Punktsymmetrie des Grafen von g2 um eben diese Fläche
kleiner ist. Daher sind die beiden betrachteten Flächen gleich groß.
2. Die Summanden heißen x und y. Es gilt also:
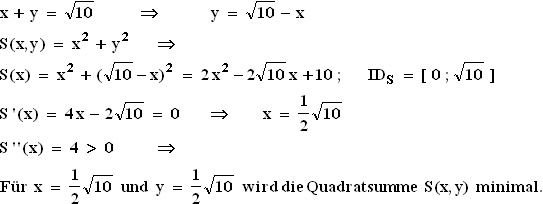
A II: Lösungen
1.1 An einer doppelten Nullstelle wechselt f '' sein Vorzeichen nicht,
d. h. der Graf von f nimmt nach dem dort vorliegenden Flachpunkt die
vorige Krümmung wieder auf und wendet sich damit nicht.
1.2 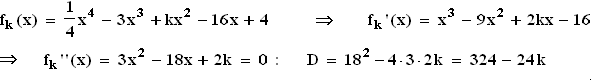 D > 0
D > 0 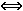 324 – 24 k > 0
324 – 24 k > 0 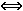 k < 13,5
k < 13,5  f hat 2 verschiedene Wendestellen:
f hat 2 verschiedene Wendestellen:
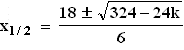 D = 0
D = 0  k = 13,5
k = 13,5  f hat keine Wendestelle, da x1/2 doppelte Nullstelle von f ''
D < 0
f hat keine Wendestelle, da x1/2 doppelte Nullstelle von f ''
D < 0  k > 13,5
k > 13,5  f hat keine Wendestelle, da f '' keine Nullstelle besitzt.
1.3 fk'(1) = 0
f hat keine Wendestelle, da f '' keine Nullstelle besitzt.
1.3 fk'(1) = 0  1 – 9 + 2k – 16 = 0
1 – 9 + 2k – 16 = 0  k = 12
1.4.1 Nach Aufgabe 1.2 gilt: f '(x) = x3 – 9x2 + 24x – 16
Nach Aufgabe 1.3 ist x0 = 1 eine Nullstelle von f '.
Die restlichen Nullstellen von f ' werden durch Polynomdivision bestimmt:
k = 12
1.4.1 Nach Aufgabe 1.2 gilt: f '(x) = x3 – 9x2 + 24x – 16
Nach Aufgabe 1.3 ist x0 = 1 eine Nullstelle von f '.
Die restlichen Nullstellen von f ' werden durch Polynomdivision bestimmt:
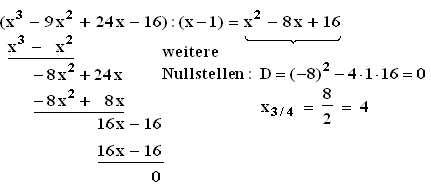 Da x3/4 eine doppelte Nullstelle von f ' ist, liegt hier kein Extrempunkt,
sondern ein TEP vor.
Nur an der einfachen Nullstelle x0 = 1 von f ' liegt ein Extrempunkt vor.
Es muss sich dabei um einen TIP handeln, da der Graf von f von oben kommt.
Seine Ordinate beträgt f (1) = –2,75.
Die Abszissen der Wendepunkte betragen für k = 12 nach Aufgabe 1.2 x1 = 4
und x2 = 2.
Art der Wendestellen:
Der Graf von f '' ist eine nach oben geöffnete Parabel, die bei x2 = 2 ihr Vor-
zeichen von + nach – und bei x1 = 4 ihr Vorzeichen von – nach + wechselt.
Da x3/4 eine doppelte Nullstelle von f ' ist, liegt hier kein Extrempunkt,
sondern ein TEP vor.
Nur an der einfachen Nullstelle x0 = 1 von f ' liegt ein Extrempunkt vor.
Es muss sich dabei um einen TIP handeln, da der Graf von f von oben kommt.
Seine Ordinate beträgt f (1) = –2,75.
Die Abszissen der Wendepunkte betragen für k = 12 nach Aufgabe 1.2 x1 = 4
und x2 = 2.
Art der Wendestellen:
Der Graf von f '' ist eine nach oben geöffnete Parabel, die bei x2 = 2 ihr Vor-
zeichen von + nach – und bei x1 = 4 ihr Vorzeichen von – nach + wechselt.
 Bei x2 = 2 liegt ein Links-Rechts-Krümmungswechsel und bei x1 = 4
ein Rechts-Links-Krümmungswechsel vor.
f (2) = 0
Bei x2 = 2 liegt ein Links-Rechts-Krümmungswechsel und bei x1 = 4
ein Rechts-Links-Krümmungswechsel vor.
f (2) = 0  WEP2(2 | 0)
f (4) = 4
WEP2(2 | 0)
f (4) = 4  WEP1(4 | 4)
1.4.2 f (0) = 4 > 0 und f (1) = –2,75 < 0
WEP1(4 | 4)
1.4.2 f (0) = 4 > 0 und f (1) = –2,75 < 0  Der Graf von f muss irgendwo zwischen
x = 0 und x = 1 die x-Achse schneiden, so dass f dort eine Nullstelle besitzt.
Newton-Verfahren: z1 = 0
Der Graf von f muss irgendwo zwischen
x = 0 und x = 1 die x-Achse schneiden, so dass f dort eine Nullstelle besitzt.
Newton-Verfahren: z1 = 0
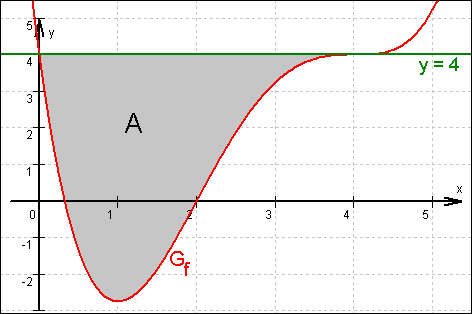
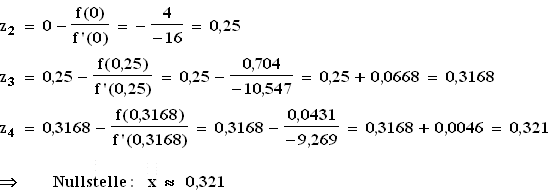 1.4.3 f (3) = 3,25 ; f (5) = 5,25
Graf von f :
1.4.3 f (3) = 3,25 ; f (5) = 5,25
Graf von f :
 1.4.4
1.4.4 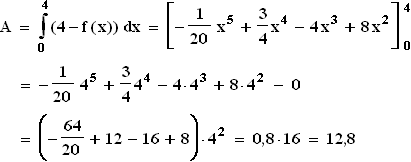 2.
2. 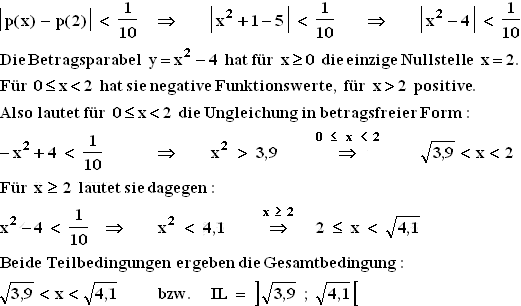 Einfacher findet man die Lösung dieser Aufgabe auf nicht rechnerischem Weg:
Die Betragsungleichung fragt nämlich nach allen x, deren Quadrate sich von der Zahl 4
um weniger als 0,1 unterscheiden. Also müssen diese Quadrate zwischen 3,9 und 4,1
liegen und damit die gesuchten x-Werte (x ≥ 0 !) zwischen
Einfacher findet man die Lösung dieser Aufgabe auf nicht rechnerischem Weg:
Die Betragsungleichung fragt nämlich nach allen x, deren Quadrate sich von der Zahl 4
um weniger als 0,1 unterscheiden. Also müssen diese Quadrate zwischen 3,9 und 4,1
liegen und damit die gesuchten x-Werte (x ≥ 0 !) zwischen 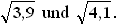 3.
3. 
 f '(x) = –x3 + 3ax2 + b
f '(x) = –x3 + 3ax2 + b  f(x) = –0,25x4 + ax3 + bx + c
WEP bei x = 2
f(x) = –0,25x4 + ax3 + bx + c
WEP bei x = 2  f ''(2) = 0
f ''(2) = 0  –12 + 12a = 0
–12 + 12a = 0  a = 1
f '(0) = –4
a = 1
f '(0) = –4  b = –4
P(2 | 0)
b = –4
P(2 | 0)  f(2) = 0
f(2) = 0  –0,25·16 + 1·8 –4·2 + c = 0
–0,25·16 + 1·8 –4·2 + c = 0  c = 4
c = 4
 f (x) = –0,25x4 + x3 – 4x + 4
1.1.2 f ''(x) = –3x2 + 6x (siehe 1.1.1);
f ''(x) = 0
f (x) = –0,25x4 + x3 – 4x + 4
1.1.2 f ''(x) = –3x2 + 6x (siehe 1.1.1);
f ''(x) = 0  –3x(x – 2) = 0
–3x(x – 2) = 0  x1 = 0
x1 = 0 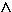 x2 = 2
x1 und x2 sind Wendestellen von f, da sie einfache Nullstellen von f '' sind.
Art der Wendestellen:
Der Graf von f '' ist eine nach unten geöffnete Parabel, die bei x1 = 0 ihr Vor-
zeichen von – nach + und bei x2 = 2 ihr Vorzeichen von + nach – wechselt.
x2 = 2
x1 und x2 sind Wendestellen von f, da sie einfache Nullstellen von f '' sind.
Art der Wendestellen:
Der Graf von f '' ist eine nach unten geöffnete Parabel, die bei x1 = 0 ihr Vor-
zeichen von – nach + und bei x2 = 2 ihr Vorzeichen von + nach – wechselt.
 Bei x1 = 0 liegt ein Rechts-Links-Krümmungswechsel und bei x2 = 2
ein Links-Rechts-Krümmungswechsel vor.
f (0) = 4
Bei x1 = 0 liegt ein Rechts-Links-Krümmungswechsel und bei x2 = 2
ein Links-Rechts-Krümmungswechsel vor.
f (0) = 4  WEP1(0 | 4)
Schon bekannt: WEP2(2 | 0)
1.1.3 f '(x) = –x3 + 3x2 – 4 (siehe 1.1.1)
Durch Probieren findet man die Nullstelle x3 = 2 von f '.
Eventuelle weitere Nullstellen ermittelt man durch Division von f '(x) durch (x – 2):
WEP1(0 | 4)
Schon bekannt: WEP2(2 | 0)
1.1.3 f '(x) = –x3 + 3x2 – 4 (siehe 1.1.1)
Durch Probieren findet man die Nullstelle x3 = 2 von f '.
Eventuelle weitere Nullstellen ermittelt man durch Division von f '(x) durch (x – 2):
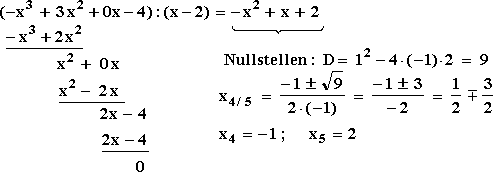 Da x3 = 2 also eine doppelte Nullstelle von f ' ist, muss dort ein Terrassenpunkt
vorliegen.
Monotonieverhalten von f :
Da x3 = 2 also eine doppelte Nullstelle von f ' ist, muss dort ein Terrassenpunkt
vorliegen.
Monotonieverhalten von f :
 HOP(–1 | 6,75)
HOP(–1 | 6,75)  Wf = ]–∞ ; 6,75]
1.1.4 f (–2) = 0; f (1) = 0,75; f (3) = –1,25
1.3.1
Wf = ]–∞ ; 6,75]
1.1.4 f (–2) = 0; f (1) = 0,75; f (3) = –1,25
1.3.1  1.2.1 gp(–x) = (–x)3 – p2(–x) = –x3 + p2x = –gp(x)
1.2.1 gp(–x) = (–x)3 – p2(–x) = –x3 + p2x = –gp(x)  Der Graf von gp ist punktsymmetrisch bzgl. O.
Nullstellen von gp:
x
Der Graf von gp ist punktsymmetrisch bzgl. O.
Nullstellen von gp:
x – p
– p x = x (x
x = x (x – p
– p ) = 0
) = 0  x
x = 0
= 0 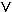 x
x = p
= p
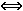 x
x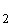

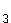 = ± p
Für p ≠ 0 besitzt gp also drei verschiedene einfache Nullstellen,
sonst eine dreifache Nullstelle x1 / 2 / 3 = 0.
1.2.2
= ± p
Für p ≠ 0 besitzt gp also drei verschiedene einfache Nullstellen,
sonst eine dreifache Nullstelle x1 / 2 / 3 = 0.
1.2.2 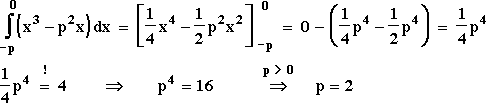 1.3.1 g2(x) = x3 – 4x
1.3.1 g2(x) = x3 – 4x  g2'(x) = 3x2 – 4
g2'(x) = 3x2 – 4  g2''(x) = 6x
g
g2''(x) = 6x
g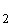 '(x) = 0
'(x) = 0  3x
3x = 4
= 4 
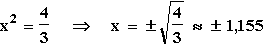 g2''(–1,155) < 0
g2''(–1,155) < 0  HOP(–1,155 | 3,08)
Wegen der Punktsymmetrie des Grafen von g2 bzgl. O muss dann gelten:
TIP(1,155 | –3,08)
1.3.2 Das Integral
HOP(–1,155 | 3,08)
Wegen der Punktsymmetrie des Grafen von g2 bzgl. O muss dann gelten:
TIP(1,155 | –3,08)
1.3.2 Das Integral 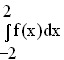 stellt geometrisch den Inhalt der Fläche zwischen G
stellt geometrisch den Inhalt der Fläche zwischen G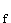 und der x-achse dar.
Diese Fläche unterscheidet sich von derjenigen zwischen den Grafen von f und g2 dadurch,
dass sie für –2 < x < 0 um die Fläche zwischen dem Grafen von g2 und der x-Achse größer
und für 0 < x < 2 wegen der Punktsymmetrie des Grafen von g2 um eben diese Fläche
kleiner ist. Daher sind die beiden betrachteten Flächen gleich groß.
2. Die Summanden heißen x und y. Es gilt also:
und der x-achse dar.
Diese Fläche unterscheidet sich von derjenigen zwischen den Grafen von f und g2 dadurch,
dass sie für –2 < x < 0 um die Fläche zwischen dem Grafen von g2 und der x-Achse größer
und für 0 < x < 2 wegen der Punktsymmetrie des Grafen von g2 um eben diese Fläche
kleiner ist. Daher sind die beiden betrachteten Flächen gleich groß.
2. Die Summanden heißen x und y. Es gilt also:
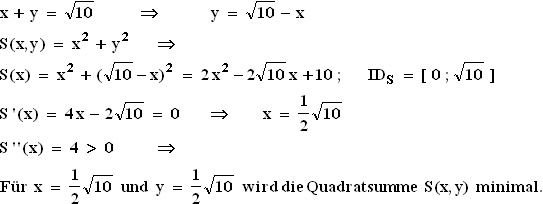
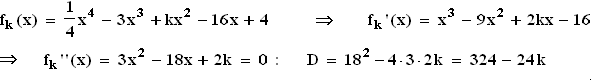 D > 0
D > 0 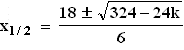 D = 0
D = 0 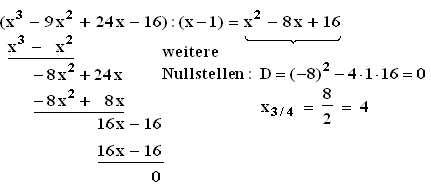 Da x3/4 eine doppelte Nullstelle von f ' ist, liegt hier kein Extrempunkt,
sondern ein TEP vor.
Nur an der einfachen Nullstelle x0 = 1 von f ' liegt ein Extrempunkt vor.
Es muss sich dabei um einen TIP handeln, da der Graf von f von oben kommt.
Seine Ordinate beträgt f (1) = –2,75.
Die Abszissen der Wendepunkte betragen für k = 12 nach Aufgabe 1.2 x1 = 4
und x2 = 2.
Art der Wendestellen:
Der Graf von f '' ist eine nach oben geöffnete Parabel, die bei x2 = 2 ihr Vor-
zeichen von + nach – und bei x1 = 4 ihr Vorzeichen von – nach + wechselt.
Da x3/4 eine doppelte Nullstelle von f ' ist, liegt hier kein Extrempunkt,
sondern ein TEP vor.
Nur an der einfachen Nullstelle x0 = 1 von f ' liegt ein Extrempunkt vor.
Es muss sich dabei um einen TIP handeln, da der Graf von f von oben kommt.
Seine Ordinate beträgt f (1) = –2,75.
Die Abszissen der Wendepunkte betragen für k = 12 nach Aufgabe 1.2 x1 = 4
und x2 = 2.
Art der Wendestellen:
Der Graf von f '' ist eine nach oben geöffnete Parabel, die bei x2 = 2 ihr Vor-
zeichen von + nach – und bei x1 = 4 ihr Vorzeichen von – nach + wechselt.
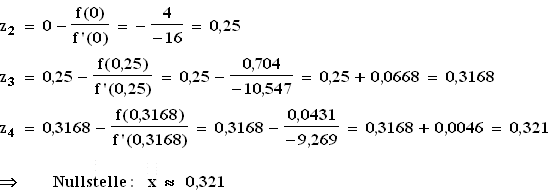 1.4.3 f (3) = 3,25 ; f (5) = 5,25
Graf von f :
1.4.3 f (3) = 3,25 ; f (5) = 5,25
Graf von f :

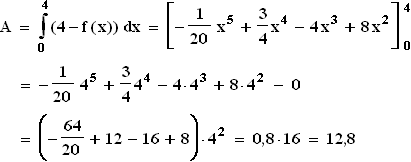
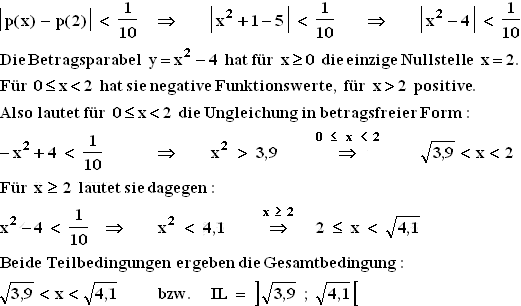 Einfacher findet man die Lösung dieser Aufgabe auf nicht rechnerischem Weg:
Die Betragsungleichung fragt nämlich nach allen x, deren Quadrate sich von der Zahl 4
um weniger als 0,1 unterscheiden. Also müssen diese Quadrate zwischen 3,9 und 4,1
liegen und damit die gesuchten x-Werte (x ≥ 0 !) zwischen
Einfacher findet man die Lösung dieser Aufgabe auf nicht rechnerischem Weg:
Die Betragsungleichung fragt nämlich nach allen x, deren Quadrate sich von der Zahl 4
um weniger als 0,1 unterscheiden. Also müssen diese Quadrate zwischen 3,9 und 4,1
liegen und damit die gesuchten x-Werte (x ≥ 0 !) zwischen 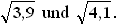 3.
3. 