p
· ( 1 – p
)
2 Das Zufallsexperiment kann als Bernoulli-Kette der Länge n =2
mit dem Parameter p angesehen werden. Dabei ist p die Wahrscheinlichkeit für einen Farbfehler bei einer einzelnen Fliese.
E: " Mindestens eine Fliese hat einen Farbfehler "
P (E ) = 1 – P ( "Keine Fliese hat einen Farbfehler" )
P (E ) = 1 –
p
· ( 1 – p
)
P (E ) = 1 – 1 · 1· ( 1– p )2
P (E ) = 1 – ( 1 – p )2
Es soll gelten P (E ) ≤ 0,0975,
somit (1-p)2 ³ 0,9025
(1 –
p)2 ≥ 0,9025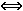 
1 – p = 1 – p
≥ 0,95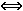
p ≤ 0,05 .
