Lösungen Aufgabengruppe 2000 SII

3.2 Für den Erwartungswert µ = E ( X ) ergibt sich:

µ = 0 · 0,4 + 1 · 0,25 + 2 · 0,15 + 3 · 0,1 + 4 · 0,05 + 5 · 0,05

µ = 1,3

Für die Varianz Var ( X ) gilt:

σ ²= Var (X) = ( 0 – 1,3 )² · 0,4 + ( 1 – 1,3 )² · 0,25 + (2 – 1,3 )² · 0,15 + ( 3 – 1,3 )² · 0,1 + ( 4 – 1,3 )² · 0,05 + ( 5 – 1,3 )² · 0,05

σ ²= Var ( X ) = 2,11 σ =

σ = 1,45.

Wegen | X – µ | < σ ( siehe Formelsammlung ) folgt:

| X – 1,3 | < 1,45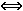

– 1,45 < X – 1,3 < 1,45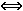

– 1,45 + 1,3 < X < 1,45 + 1,3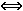

– 0,15 < X < 2,75

P ( | X – µ | < σ ) = W (0) + W (1) + W (2)

P ( | X – µ | < σ ) = 0,4 + 0,25 + 0,15 = 0,8