Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2001
S I: Lösungen
1. Vierfeldertafel (gegebene Werte in Fettschrift):
|
|
D
|
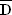
|
|
|
L
|
0,03
|
0,17
|
0,2
|
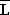
|
0,28
|
0,52
|
0,8
|
|
|
0,31
|
0,69
|
1
|
Aus der Vierfeldertafel folgt:
a) P(A) = P(L  D) = 0,03 ;
A: „Es handelt sich um einen von einer Dame gesteuerten LKW.“
b) P(B) = P(L
D) = 0,03 ;
A: „Es handelt sich um einen von einer Dame gesteuerten LKW.“
b) P(B) = P(L 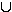
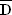 ) = P(L) + P(
) = P(L) + P(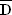 ) – P(L
) – P(L 
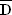 ) = 0,2 + 0,69 – 0,17 = 0,72 ;
B: „Es handelt sich um einen LKW oder es sitzt keine Dame am Steuer.“
Sprachlich eleganter:
„Es handelt sich nicht um einen von einer Dame gesteuerten PKW.“
c) P(C) = P(
) = 0,2 + 0,69 – 0,17 = 0,72 ;
B: „Es handelt sich um einen LKW oder es sitzt keine Dame am Steuer.“
Sprachlich eleganter:
„Es handelt sich nicht um einen von einer Dame gesteuerten PKW.“
c) P(C) = P( ) = 1 – P(L
) = 1 – P(L 
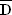 ) = 1 – 0,17 = 0,83 ;
C: „Es handelt sich nicht um einen von einem Herrn gesteuerten LKW.“
2. P(L
) = 1 – 0,17 = 0,83 ;
C: „Es handelt sich nicht um einen von einem Herrn gesteuerten LKW.“
2. P(L  D) = 0,03 ≠ P(L) · P(D) = 0,2 · 0,31 = 0,062
D) = 0,03 ≠ P(L) · P(D) = 0,2 · 0,31 = 0,062  Die Ereignisse L und D sind stochastisch abhängig.
3.1
Die Ereignisse L und D sind stochastisch abhängig.
3.1 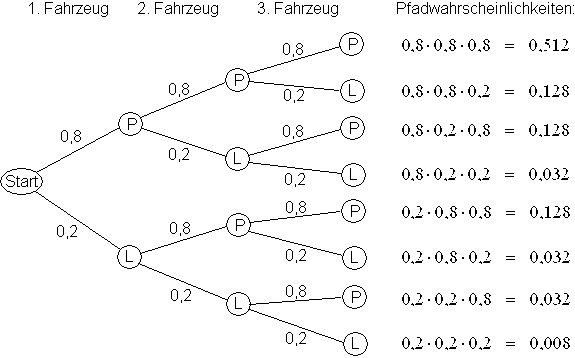
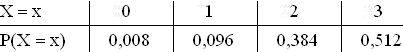
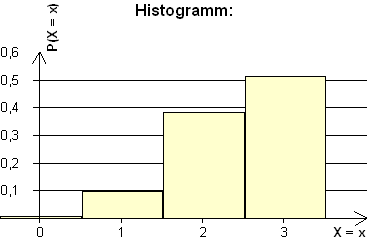 3.2
3.2 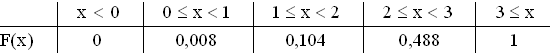 F(2) = 0,488 bedeutet:
Die Wahrscheinlichkeit, dass bei 3 aufeinander folgenden Fahrzeugen höchstens
2 PKWs dabei sind, beträgt 0,488.
4.1 P(E1) = 0,89 · 0,2 = 0,027
P(E2) = B(10 , 0,2 ; 5) = 0,026 (Tafelwerk)
P(E3) = P(PLPLPLPLPL) + P(LPLPLPLPLP) = 0,85 · 0,25 · 2 = 0,0002
4.2 P(X ≥ 1) =
F(2) = 0,488 bedeutet:
Die Wahrscheinlichkeit, dass bei 3 aufeinander folgenden Fahrzeugen höchstens
2 PKWs dabei sind, beträgt 0,488.
4.1 P(E1) = 0,89 · 0,2 = 0,027
P(E2) = B(10 , 0,2 ; 5) = 0,026 (Tafelwerk)
P(E3) = P(PLPLPLPLPL) + P(LPLPLPLPLP) = 0,85 · 0,25 · 2 = 0,0002
4.2 P(X ≥ 1) = 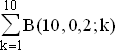 = 1 – B(10 , 0,2 ; 0) = 1 – 0,107 = 0,893
4.3
= 1 – B(10 , 0,2 ; 0) = 1 – 0,107 = 0,893
4.3 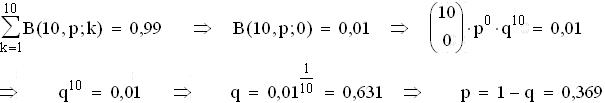 5. H0: p = 0,2 ; H1: p > 0,2
Testgröße T = Anzahl der LKWs in den 200 zufällig ausgewählten Fahrzeugen = 45
Ablehnungsbereich T1 = { k ; ... ; 200 | P(T ≥ k) ≤ 0,05 }
P(T ≥ k) ≤ 0,05
P(T ≤ k–1) ≥ 0,95
k – 1 ≥ 49 (Tafelwerk)
k ≥ 50
5. H0: p = 0,2 ; H1: p > 0,2
Testgröße T = Anzahl der LKWs in den 200 zufällig ausgewählten Fahrzeugen = 45
Ablehnungsbereich T1 = { k ; ... ; 200 | P(T ≥ k) ≤ 0,05 }
P(T ≥ k) ≤ 0,05
P(T ≤ k–1) ≥ 0,95
k – 1 ≥ 49 (Tafelwerk)
k ≥ 50  T1 = { 50, ... , 200 }
Auf dem 5%-Niveau könnte also erst ab 50 gezählten LKWs die Nullhypothese H0
abgelehnt werden.
45
T1 = { 50, ... , 200 }
Auf dem 5%-Niveau könnte also erst ab 50 gezählten LKWs die Nullhypothese H0
abgelehnt werden.
45 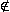 T1
T1  Die Annahme, dass der Prozentsatz der LKWs nahezu gleich geblieben ist,
kann auf dem 5%-Niveau nicht abgelehnt werden.
Die Annahme, dass der Prozentsatz der LKWs nahezu gleich geblieben ist,
kann auf dem 5%-Niveau nicht abgelehnt werden.
S II: Lösungen
1.1 P = 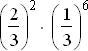 = 0,0006
1.2 P(X ≥ 6) =
= 0,0006
1.2 P(X ≥ 6) = 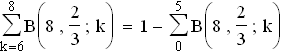 = 1 – F(5) = 1 – 0,5318 = 0,4682
1.3 P = 1 – P(X = 0) – P(X = 6) = 1 – 0,00015 – 0,27313 = 0,7267 (Tafelwerk)
2. Gewinnereignisse für Herrn Molle:
G1 = { (1 ; 5) , (5 ; 1) , (2 ; 6) , (6 ; 2) } :
P(G
= 1 – F(5) = 1 – 0,5318 = 0,4682
1.3 P = 1 – P(X = 0) – P(X = 6) = 1 – 0,00015 – 0,27313 = 0,7267 (Tafelwerk)
2. Gewinnereignisse für Herrn Molle:
G1 = { (1 ; 5) , (5 ; 1) , (2 ; 6) , (6 ; 2) } :
P(G ) =
) = 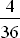 ; Gewinn X = 4 DM
G2 = { (1 ; 3) , (3 ; 1) , (2 ; 4) , (4 ; 2) , (3 ; 5) , (5 ; 3) , (4 ; 6) , (6 ; 4) } :
P(G
; Gewinn X = 4 DM
G2 = { (1 ; 3) , (3 ; 1) , (2 ; 4) , (4 ; 2) , (3 ; 5) , (5 ; 3) , (4 ; 6) , (6 ; 4) } :
P(G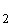 ) =
) = 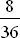 ; Gewinn X = 2 DM
„Neutrales“ Ereignis für Herrn Molle:
N = { (1 ; 1) , (2 ; 2) , (3 ; 3) , (4 ; 4) , (5 ; 5) , (6 ; 6) } :
P(N) =
; Gewinn X = 2 DM
„Neutrales“ Ereignis für Herrn Molle:
N = { (1 ; 1) , (2 ; 2) , (3 ; 3) , (4 ; 4) , (5 ; 5) , (6 ; 6) } :
P(N) = 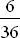 ; Gewinn X = 0 DM
Verlustereignisse für Herrn Molle:
V1 = { (1 ; 2) , (2 ; 1) , (2 ; 3) , (3 ; 2) , (3 ; 4) , (4 ; 3) , (4 ; 5) , (5 ; 4) , (5 ; 6) , (6 ; 5) } :
P(V
; Gewinn X = 0 DM
Verlustereignisse für Herrn Molle:
V1 = { (1 ; 2) , (2 ; 1) , (2 ; 3) , (3 ; 2) , (3 ; 4) , (4 ; 3) , (4 ; 5) , (5 ; 4) , (5 ; 6) , (6 ; 5) } :
P(V ) =
) = 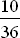 ; Verlust X = 1 DM
V2 = { (1 ; 4) , (4 ; 1) , (2 ; 5) , (5 ; 2) , (3 ; 6) , (6 ; 3) } :
P(V
; Verlust X = 1 DM
V2 = { (1 ; 4) , (4 ; 1) , (2 ; 5) , (5 ; 2) , (3 ; 6) , (6 ; 3) } :
P(V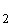 ) =
) = 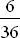 ; Verlust X = 3 DM
V3 = { (1 ; 6) , (6 ; 1) } :
P(V
; Verlust X = 3 DM
V3 = { (1 ; 6) , (6 ; 1) } :
P(V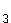 ) =
) = 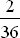 ; Verlust X = 5 DM
Also ergibt sich die Wahrscheinlichkeitsverteilung
; Verlust X = 5 DM
Also ergibt sich die Wahrscheinlichkeitsverteilung
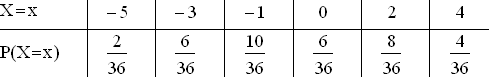 und daraus die kumulative Verteilungsfunktion
und daraus die kumulative Verteilungsfunktion
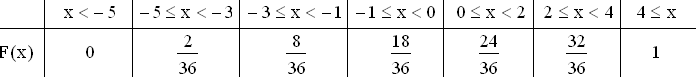 mit ihrem Grafen
mit ihrem Grafen
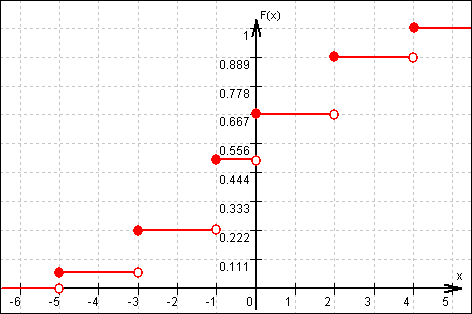 3. P(„Dame geht“) = 1 – P(„Dame bleibt“) =
3. P(„Dame geht“) = 1 – P(„Dame bleibt“) =
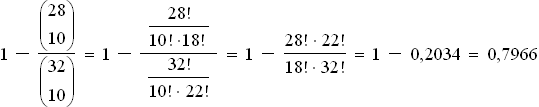 4.1 Testgröße T = Anzahl der Treffer bei 30 Schuss
Testart: zweiseitiger Hypothesentest
H
4.1 Testgröße T = Anzahl der Treffer bei 30 Schuss
Testart: zweiseitiger Hypothesentest
H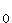 : p =
: p = 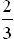 Annahmebereich T
Annahmebereich T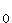 = [18 ; 22]
= [18 ; 22]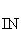 ; Ablehnungsbereich T
; Ablehnungsbereich T = [0 ; 17]
= [0 ; 17]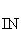
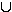 [23 ; 30]
[23 ; 30]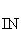 P(T ≤ 17) = 0,16601 (Tafelwerk);
P(T ≥ 23) = 1 – P(T ≤ 22) = 1 – 0,83322 (Tafelwerk) = 0,16678
P(T ≤ 17) = 0,16601 (Tafelwerk);
P(T ≥ 23) = 1 – P(T ≤ 22) = 1 – 0,83322 (Tafelwerk) = 0,16678
 P(T
P(T  T1) = 0,16601 + 0,16678 = 0,333
4.2 Annahmebereich T0 = [20 – k ; 20 + k]
T1) = 0,16601 + 0,16678 = 0,333
4.2 Annahmebereich T0 = [20 – k ; 20 + k]
 P(T ≤ 20 – k – 1) ≤ 0,025
20 – k – 1 ≤ 14 (Tafelwerk)
k ≥ 5
P(T ≤ 20 – k – 1) ≤ 0,025
20 – k – 1 ≤ 14 (Tafelwerk)
k ≥ 5
 kleinstes T0 = [15 ; 25]
kleinstes T0 = [15 ; 25] Überprüfung der rechten Grenze:
P(T > 25) = 1 – P(T ≤ 25) = 1 – 0,988 = 0,012 < 0,025, also o.K.
5.1 P(Y ≤ 2) = 0,70
Überprüfung der rechten Grenze:
P(T > 25) = 1 – P(T ≤ 25) = 1 – 0,988 = 0,012 < 0,025, also o.K.
5.1 P(Y ≤ 2) = 0,70  a + 0,40 + 0,25 = 0,70
a + 0,40 + 0,25 = 0,70  a = 0,05
0,70 + a + b + b + 0,05 = 1
a = 0,05
0,70 + a + b + b + 0,05 = 1  2b = 0,25 – a = 0,20
2b = 0,25 – a = 0,20  b = 0,10
5.2 Erwartungswert E(Y) = 0,40 + 2·0,25 + 3·0,15 + 4·0,10 + 5·0,05 = 2
5.3 Var (Y) = E(Y2) – [E(Y)]2 = 0,40 + 4·0,25 + 9·0,15 + 16·0,10 + 25·0,05 – 4 = 1,6
b = 0,10
5.2 Erwartungswert E(Y) = 0,40 + 2·0,25 + 3·0,15 + 4·0,10 + 5·0,05 = 2
5.3 Var (Y) = E(Y2) – [E(Y)]2 = 0,40 + 4·0,25 + 9·0,15 + 16·0,10 + 25·0,05 – 4 = 1,6

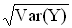 = 1,265
P(|Y – E(Y)| ≤
= 1,265
P(|Y – E(Y)| ≤ 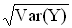 )
P(2–1,265 ≤ Y ≤ 2+1,265) = P(1 ≤ Y ≤ 3) = 0,40 + 0,25 + 0,15 = 0,8
)
P(2–1,265 ≤ Y ≤ 2+1,265) = P(1 ≤ Y ≤ 3) = 0,40 + 0,25 + 0,15 = 0,8
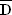
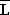
 D) = 0,03 ;
A: „Es handelt sich um einen von einer Dame gesteuerten LKW.“
b) P(B) = P(L
D) = 0,03 ;
A: „Es handelt sich um einen von einer Dame gesteuerten LKW.“
b) P(B) = P(L 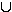
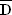 ) = P(L) + P(
) = P(L) + P(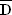 ) – P(L
) – P(L 
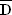 ) = 0,2 + 0,69 – 0,17 = 0,72 ;
B: „Es handelt sich um einen LKW oder es sitzt keine Dame am Steuer.“
Sprachlich eleganter:
„Es handelt sich nicht um einen von einer Dame gesteuerten PKW.“
c) P(C) = P(
) = 0,2 + 0,69 – 0,17 = 0,72 ;
B: „Es handelt sich um einen LKW oder es sitzt keine Dame am Steuer.“
Sprachlich eleganter:
„Es handelt sich nicht um einen von einer Dame gesteuerten PKW.“
c) P(C) = P( ) = 1 – P(L
) = 1 – P(L 
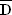 ) = 1 – 0,17 = 0,83 ;
C: „Es handelt sich nicht um einen von einem Herrn gesteuerten LKW.“
2. P(L
) = 1 – 0,17 = 0,83 ;
C: „Es handelt sich nicht um einen von einem Herrn gesteuerten LKW.“
2. P(L  D) = 0,03 ≠ P(L) · P(D) = 0,2 · 0,31 = 0,062
D) = 0,03 ≠ P(L) · P(D) = 0,2 · 0,31 = 0,062  Die Ereignisse L und D sind stochastisch abhängig.
3.1
Die Ereignisse L und D sind stochastisch abhängig.
3.1 
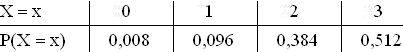
 3.2
3.2 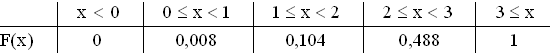 F(2) = 0,488 bedeutet:
Die Wahrscheinlichkeit, dass bei 3 aufeinander folgenden Fahrzeugen höchstens
2 PKWs dabei sind, beträgt 0,488.
4.1 P(E1) = 0,89 · 0,2 = 0,027
P(E2) = B(10 , 0,2 ; 5) = 0,026 (Tafelwerk)
P(E3) = P(PLPLPLPLPL) + P(LPLPLPLPLP) = 0,85 · 0,25 · 2 = 0,0002
4.2 P(X ≥ 1) =
F(2) = 0,488 bedeutet:
Die Wahrscheinlichkeit, dass bei 3 aufeinander folgenden Fahrzeugen höchstens
2 PKWs dabei sind, beträgt 0,488.
4.1 P(E1) = 0,89 · 0,2 = 0,027
P(E2) = B(10 , 0,2 ; 5) = 0,026 (Tafelwerk)
P(E3) = P(PLPLPLPLPL) + P(LPLPLPLPLP) = 0,85 · 0,25 · 2 = 0,0002
4.2 P(X ≥ 1) = 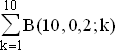 = 1 – B(10 , 0,2 ; 0) = 1 – 0,107 = 0,893
4.3
= 1 – B(10 , 0,2 ; 0) = 1 – 0,107 = 0,893
4.3 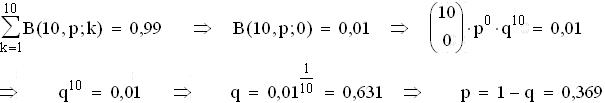 5. H0: p = 0,2 ; H1: p > 0,2
Testgröße T = Anzahl der LKWs in den 200 zufällig ausgewählten Fahrzeugen = 45
Ablehnungsbereich T1 = { k ; ... ; 200 | P(T ≥ k) ≤ 0,05 }
P(T ≥ k) ≤ 0,05
P(T ≤ k–1) ≥ 0,95
k – 1 ≥ 49 (Tafelwerk)
k ≥ 50
5. H0: p = 0,2 ; H1: p > 0,2
Testgröße T = Anzahl der LKWs in den 200 zufällig ausgewählten Fahrzeugen = 45
Ablehnungsbereich T1 = { k ; ... ; 200 | P(T ≥ k) ≤ 0,05 }
P(T ≥ k) ≤ 0,05
P(T ≤ k–1) ≥ 0,95
k – 1 ≥ 49 (Tafelwerk)
k ≥ 50  T1 = { 50, ... , 200 }
Auf dem 5%-Niveau könnte also erst ab 50 gezählten LKWs die Nullhypothese H0
abgelehnt werden.
45
T1 = { 50, ... , 200 }
Auf dem 5%-Niveau könnte also erst ab 50 gezählten LKWs die Nullhypothese H0
abgelehnt werden.
45 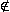 T1
T1  Die Annahme, dass der Prozentsatz der LKWs nahezu gleich geblieben ist,
kann auf dem 5%-Niveau nicht abgelehnt werden.
Die Annahme, dass der Prozentsatz der LKWs nahezu gleich geblieben ist,
kann auf dem 5%-Niveau nicht abgelehnt werden.
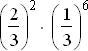 = 0,0006
1.2 P(X ≥ 6) =
= 0,0006
1.2 P(X ≥ 6) = 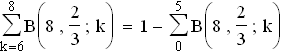 = 1 – F(5) = 1 – 0,5318 = 0,4682
1.3 P = 1 – P(X = 0) – P(X = 6) = 1 – 0,00015 – 0,27313 = 0,7267 (Tafelwerk)
2. Gewinnereignisse für Herrn Molle:
G1 = { (1 ; 5) , (5 ; 1) , (2 ; 6) , (6 ; 2) } :
P(G
= 1 – F(5) = 1 – 0,5318 = 0,4682
1.3 P = 1 – P(X = 0) – P(X = 6) = 1 – 0,00015 – 0,27313 = 0,7267 (Tafelwerk)
2. Gewinnereignisse für Herrn Molle:
G1 = { (1 ; 5) , (5 ; 1) , (2 ; 6) , (6 ; 2) } :
P(G ) =
) = 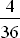 ; Gewinn X = 4 DM
G2 = { (1 ; 3) , (3 ; 1) , (2 ; 4) , (4 ; 2) , (3 ; 5) , (5 ; 3) , (4 ; 6) , (6 ; 4) } :
P(G
; Gewinn X = 4 DM
G2 = { (1 ; 3) , (3 ; 1) , (2 ; 4) , (4 ; 2) , (3 ; 5) , (5 ; 3) , (4 ; 6) , (6 ; 4) } :
P(G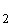 ) =
) = 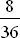 ; Gewinn X = 2 DM
„Neutrales“ Ereignis für Herrn Molle:
N = { (1 ; 1) , (2 ; 2) , (3 ; 3) , (4 ; 4) , (5 ; 5) , (6 ; 6) } :
P(N) =
; Gewinn X = 2 DM
„Neutrales“ Ereignis für Herrn Molle:
N = { (1 ; 1) , (2 ; 2) , (3 ; 3) , (4 ; 4) , (5 ; 5) , (6 ; 6) } :
P(N) = 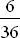 ; Gewinn X = 0 DM
Verlustereignisse für Herrn Molle:
V1 = { (1 ; 2) , (2 ; 1) , (2 ; 3) , (3 ; 2) , (3 ; 4) , (4 ; 3) , (4 ; 5) , (5 ; 4) , (5 ; 6) , (6 ; 5) } :
P(V
; Gewinn X = 0 DM
Verlustereignisse für Herrn Molle:
V1 = { (1 ; 2) , (2 ; 1) , (2 ; 3) , (3 ; 2) , (3 ; 4) , (4 ; 3) , (4 ; 5) , (5 ; 4) , (5 ; 6) , (6 ; 5) } :
P(V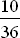 ; Verlust X = 1 DM
V2 = { (1 ; 4) , (4 ; 1) , (2 ; 5) , (5 ; 2) , (3 ; 6) , (6 ; 3) } :
P(V
; Verlust X = 1 DM
V2 = { (1 ; 4) , (4 ; 1) , (2 ; 5) , (5 ; 2) , (3 ; 6) , (6 ; 3) } :
P(V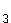 ) =
) = 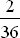 ; Verlust X = 5 DM
Also ergibt sich die Wahrscheinlichkeitsverteilung
; Verlust X = 5 DM
Also ergibt sich die Wahrscheinlichkeitsverteilung
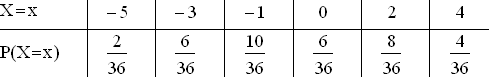 und daraus die kumulative Verteilungsfunktion
und daraus die kumulative Verteilungsfunktion
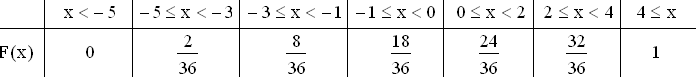 mit ihrem Grafen
mit ihrem Grafen
 3. P(„Dame geht“) = 1 – P(„Dame bleibt“) =
3. P(„Dame geht“) = 1 – P(„Dame bleibt“) =
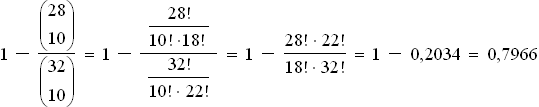 4.1 Testgröße T = Anzahl der Treffer bei 30 Schuss
Testart: zweiseitiger Hypothesentest
H
4.1 Testgröße T = Anzahl der Treffer bei 30 Schuss
Testart: zweiseitiger Hypothesentest
H : p =
: p = 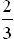 Annahmebereich T
Annahmebereich T ; Ablehnungsbereich T
; Ablehnungsbereich T T1) = 0,16601 + 0,16678 = 0,333
4.2 Annahmebereich T0 = [20 – k ; 20 + k]
T1) = 0,16601 + 0,16678 = 0,333
4.2 Annahmebereich T0 = [20 – k ; 20 + k]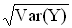 = 1,265
P(|Y – E(Y)| ≤
= 1,265
P(|Y – E(Y)| ≤