Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2002
S I: Lösungen
1.1 P(Z) = 1 – P(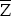 ) = 1 – 0,5 = 0,5 ; P(F) = 1 – P(
) = 1 – 0,5 = 0,5 ; P(F) = 1 – P(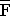 ) = 1 – 0,3 = 0,7 ;
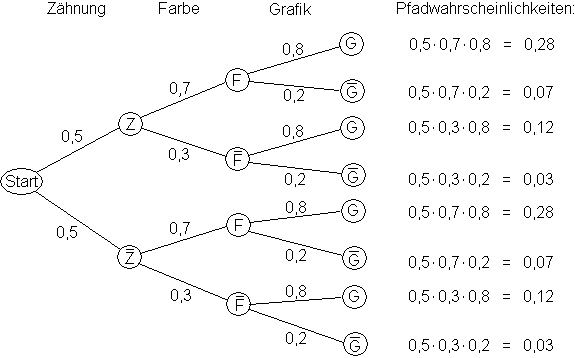
P(ZFG) = P(Z) · P(F) · P(G) = 0,5 · 0,7 · P(G) = 0,28
) = 1 – 0,3 = 0,7 ;
P(ZFG) = P(Z) · P(F) · P(G) = 0,5 · 0,7 · P(G) = 0,28
 0,35 · P(G) = 0,28
0,35 · P(G) = 0,28  P(G) = 0,8
P(G) = 0,8  P(
P(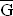 ) = 1 – 0,8 = 0,2
) = 1 – 0,8 = 0,2
 1.2 E1 = { Z
1.2 E1 = { Z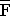
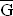 ;
; 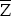 }
}  P(E1) = 0,03 + 0,5 = 0,53
E2 = {
P(E1) = 0,03 + 0,5 = 0,53
E2 = { 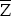 FG ; Z
FG ; Z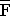 G ; ZF
G ; ZF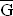 }
}  P(E2) = 0,28 + 0,12 + 0,07 = 0,47
E1
P(E2) = 0,28 + 0,12 + 0,07 = 0,47
E1  E2 = {
E2 = { 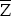 FG }
FG }  P(E1
P(E1  E2) = 0,28
P(E1
E2) = 0,28
P(E1  E2) = P(E1) · P(E2) ?
0,28 ≠ 0,53 · 0,47
E2) = P(E1) · P(E2) ?
0,28 ≠ 0,53 · 0,47  E1 und E2 sind stochastisch abhängig.
2.1 0,4a + 0,025a2 + 0,05 + 0,05 = 1
0,025a2 + 0,4a – 0,9 = 0 | · 40
a2 + 16a – 36 = 0
(a + 18) (a – 2) = 0
E1 und E2 sind stochastisch abhängig.
2.1 0,4a + 0,025a2 + 0,05 + 0,05 = 1
0,025a2 + 0,4a – 0,9 = 0 | · 40
a2 + 16a – 36 = 0
(a + 18) (a – 2) = 0  a = 2
(a = –18 scheidet aus, da es keine negativen Wahrscheinlichkeiten gibt.)
2.2 E(X) = 0·0,4·2 + 1·0,025·22 + 2·0,05 + 3·0,05 = 0,35
E(X2) = 0·0,4·2 + 1·0,025·22 + 4·0,05 + 9·0,05 = 0,75
Var(X) = E(X2) – (E(X))2 = 0,75 – 0,352 = 0,6275
a = 2
(a = –18 scheidet aus, da es keine negativen Wahrscheinlichkeiten gibt.)
2.2 E(X) = 0·0,4·2 + 1·0,025·22 + 2·0,05 + 3·0,05 = 0,35
E(X2) = 0·0,4·2 + 1·0,025·22 + 4·0,05 + 9·0,05 = 0,75
Var(X) = E(X2) – (E(X))2 = 0,75 – 0,352 = 0,6275  σ =
σ = 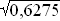 = 0,792
P(E(X)–2σ ≤ X ≤ E(X)+2σ) = P(–1,23 ≤ X ≤ 1,93)
= P(X = 0
= 0,792
P(E(X)–2σ ≤ X ≤ E(X)+2σ) = P(–1,23 ≤ X ≤ 1,93)
= P(X = 0 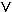 X = 1) = 0,8 + 0,1 = 0,9
2.3 p = P(X = 0) = 0,8 ; n = 200
X = 1) = 0,8 + 0,1 = 0,9
2.3 p = P(X = 0) = 0,8 ; n = 200  P(150 ≤ X ≤ 170) = F(170) – F(149) = 0,9717 – 0,0345 = 0,9372
2.4
P(150 ≤ X ≤ 170) = F(170) – F(149) = 0,9717 – 0,0345 = 0,9372
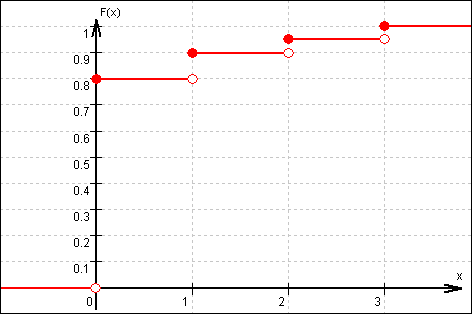
2.4 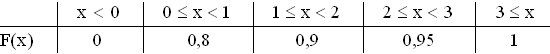 Graf der kumulativen Verteilungsfunktion F:
Graf der kumulativen Verteilungsfunktion F:
 k = 1 – F(2,3) = 1 – F(2) = 1 – 0,95 = 0,05 bedeutet die Wahrscheinlichkeit,
dass bei einer zufällig ausgewählten Briefmarke des neuen Drucks mehr als
zwei Fehler auftreten.
3.1 Var(X) = σ2 = n·p·q = n·p·(1–p)
k = 1 – F(2,3) = 1 – F(2) = 1 – 0,95 = 0,05 bedeutet die Wahrscheinlichkeit,
dass bei einer zufällig ausgewählten Briefmarke des neuen Drucks mehr als
zwei Fehler auftreten.
3.1 Var(X) = σ2 = n·p·q = n·p·(1–p)  8100 = 90000 (p – p2)
8100 = 90000 (p – p2)  0,09 = p – p2
0,09 = p – p2  p2 – p + 0,09 = 0 D = 1 – 0,36 = 0,64
p2 – p + 0,09 = 0 D = 1 – 0,36 = 0,64 
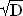 = 0,8
= 0,8  p1 / 2 = 0,5 ± 0,4
p1 / 2 = 0,5 ± 0,4  p1 = 0,9 ; p2 = 0,1
Gilt p = 0,1, dann werden insgesamt mehr fehlerfreie als fehlerhafte
Briefmarken gedruckt.
3.2 µ = n · p = 90000 · 0,1 = 9000
Mit 9000 fehlerhaften Marken ist zu rechnen.
4. Testgröße T: Anzahl der fehlerhaften Briefmarken in der Stichprobe der Länge 200.
Testart: einseitiger (rechtsseitiger) Signifikanztest
Nullhypothese H0: p = 0,05 (Gegenhypothese H1: p > 0,05)
Ablehnungsbereich: T1 = [k ; 200]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≥ k) < 0,01
p1 = 0,9 ; p2 = 0,1
Gilt p = 0,1, dann werden insgesamt mehr fehlerfreie als fehlerhafte
Briefmarken gedruckt.
3.2 µ = n · p = 90000 · 0,1 = 9000
Mit 9000 fehlerhaften Marken ist zu rechnen.
4. Testgröße T: Anzahl der fehlerhaften Briefmarken in der Stichprobe der Länge 200.
Testart: einseitiger (rechtsseitiger) Signifikanztest
Nullhypothese H0: p = 0,05 (Gegenhypothese H1: p > 0,05)
Ablehnungsbereich: T1 = [k ; 200]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≥ k) < 0,01  P(T ≤ k–1) > 0,99
k – 1 ≥ 18 (Tafelwerk)
k ≥ 19
P(T ≤ k–1) > 0,99
k – 1 ≥ 18 (Tafelwerk)
k ≥ 19  T1 = [19 ; 200]IN
Ab 19 fehlerhaften Briefmarken in der Stichprobe darf die Nullhypothese auf dem
1%-Niveau abgelehnt werden.
T1 = [19 ; 200]IN
Ab 19 fehlerhaften Briefmarken in der Stichprobe darf die Nullhypothese auf dem
1%-Niveau abgelehnt werden.
S II: Lösungen
1.1 kJ = Anzahl der jungen konservativen Anleger;
kM = Anzahl der konservativen Anleger mittleren Alters; kM = 3·kJ
kS = Anzahl der konservativen Anleger unter den Senioren; kS = 320.
Es gilt: kJ + kM + kS = 800
kJ + 3·kJ + 320 = 800
4·kJ = 480
kJ = 120
1.2 rJ = Anzahl der jungen risikofreudigen Anleger; rJ = 690 – 120 = 570
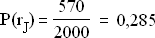 1.3
1.3 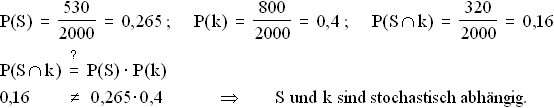 2.1 |Ω| = 5! = 120
2.2
2.1 |Ω| = 5! = 120
2.2 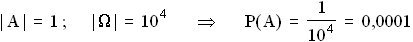 3.1 Es liegt eine Binomialverteilung mit n = 50 und p = 0,7 vor.
3.1 Es liegt eine Binomialverteilung mit n = 50 und p = 0,7 vor.  µ = n · p = 50 · 0,7 = 35
Var(X) = n · p · q = 35 · 0,3 = 10,5
σ =
µ = n · p = 50 · 0,7 = 35
Var(X) = n · p · q = 35 · 0,3 = 10,5
σ = 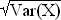 = 3,24
P(µ–σ ≤ X ≤ µ+σ) = P(31,76 ≤ X ≤ 38,24) = P(32 ≤ X ≤ 38)
= F(38) – F(31) = 0,861 – 0,141 = 0,72
3.2 Mindestens 15 PCs sind genau dann frei, wenn höchstens 35 PCs belegt sind.
P(X ≤ 35) = 0,553
4.1 Testart: einseitiger (linksseitiger) Signifikanztest (H0: p = 0,6 ; H1: p < 0,6)
Testgröße T: Anzahl der Internetnutzer aus der Stichprobe der Länge 200,
die über A surfen.
Ablehnungsbereich: T1 = [0 ; k]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≤ k) < 0,05
= 3,24
P(µ–σ ≤ X ≤ µ+σ) = P(31,76 ≤ X ≤ 38,24) = P(32 ≤ X ≤ 38)
= F(38) – F(31) = 0,861 – 0,141 = 0,72
3.2 Mindestens 15 PCs sind genau dann frei, wenn höchstens 35 PCs belegt sind.
P(X ≤ 35) = 0,553
4.1 Testart: einseitiger (linksseitiger) Signifikanztest (H0: p = 0,6 ; H1: p < 0,6)
Testgröße T: Anzahl der Internetnutzer aus der Stichprobe der Länge 200,
die über A surfen.
Ablehnungsbereich: T1 = [0 ; k]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≤ k) < 0,05  k ≤ 108 (Tafelwerk)
k ≤ 108 (Tafelwerk)  T1 = [0 ; 108]IN
Bis 108 Internetnutzer in der Stichprobe, die einen anderen Provider haben,
darf die Nullhypothese auf dem 5%-Niveau abgelehnt werden.
Der Fehler zweiter Art liegt hier vor, wenn auf Grund der Tatsache, dass höchstens
108 Internetnutzer mit Provider A in der Stichprobe sind, die Nullhaypothese p = 0,6
abgelehnt wird, obwohl sie in Wirklichkeit stimmt.
4.2 Angenommen, in der Stichprobe sind tatsächlich 112 Internetnutzer mit Provider A.
Da das Testergebnis nicht im Ablehnungsbereich [0 ; 108]IN liegt, darf die Null-
hypothese p = 0,6 auf dem 5%-Niveau nicht abgelehnt werden.
5.1
T1 = [0 ; 108]IN
Bis 108 Internetnutzer in der Stichprobe, die einen anderen Provider haben,
darf die Nullhypothese auf dem 5%-Niveau abgelehnt werden.
Der Fehler zweiter Art liegt hier vor, wenn auf Grund der Tatsache, dass höchstens
108 Internetnutzer mit Provider A in der Stichprobe sind, die Nullhaypothese p = 0,6
abgelehnt wird, obwohl sie in Wirklichkeit stimmt.
4.2 Angenommen, in der Stichprobe sind tatsächlich 112 Internetnutzer mit Provider A.
Da das Testergebnis nicht im Ablehnungsbereich [0 ; 108]IN liegt, darf die Null-
hypothese p = 0,6 auf dem 5%-Niveau nicht abgelehnt werden.
5.1
|
x
|
10000
|
500
|
20
|
0
|
|
P(X = x)
|
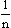
|
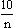
|
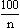
|
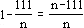
|
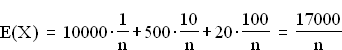 5.2
5.2 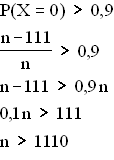 Ab n = 1111 Abonnenten wäre die Wahrscheinlichkeit, keinen Gewinn zu erzielen,
größer als 90%.
Ab n = 1111 Abonnenten wäre die Wahrscheinlichkeit, keinen Gewinn zu erzielen,
größer als 90%.
 ) = 1 – 0,5 = 0,5 ; P(F) = 1 – P(
) = 1 – 0,5 = 0,5 ; P(F) = 1 – P( ) = 1 – 0,3 = 0,7 ;
P(ZFG) = P(Z) · P(F) · P(G) = 0,5 · 0,7 · P(G) = 0,28
) = 1 – 0,3 = 0,7 ;
P(ZFG) = P(Z) · P(F) · P(G) = 0,5 · 0,7 · P(G) = 0,28
 0,35 · P(G) = 0,28
0,35 · P(G) = 0,28  P(G) = 0,8
P(G) = 0,8  P(
P(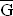 ) = 1 – 0,8 = 0,2
) = 1 – 0,8 = 0,2
 1.2 E1 = { Z
1.2 E1 = { Z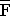
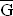 ;
; 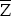 }
}  P(E1) = 0,03 + 0,5 = 0,53
E2 = {
P(E1) = 0,03 + 0,5 = 0,53
E2 = { 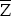 FG ; Z
FG ; Z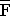 G ; ZF
G ; ZF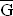 }
}  P(E2) = 0,28 + 0,12 + 0,07 = 0,47
E1
P(E2) = 0,28 + 0,12 + 0,07 = 0,47
E1  E2 = {
E2 = { 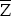 FG }
FG }  P(E1
P(E1  E2) = 0,28
P(E1
E2) = 0,28
P(E1  E2) = P(E1) · P(E2) ?
0,28 ≠ 0,53 · 0,47
E2) = P(E1) · P(E2) ?
0,28 ≠ 0,53 · 0,47  E1 und E2 sind stochastisch abhängig.
2.1 0,4a + 0,025a2 + 0,05 + 0,05 = 1
0,025a2 + 0,4a – 0,9 = 0 | · 40
a2 + 16a – 36 = 0
(a + 18) (a – 2) = 0
E1 und E2 sind stochastisch abhängig.
2.1 0,4a + 0,025a2 + 0,05 + 0,05 = 1
0,025a2 + 0,4a – 0,9 = 0 | · 40
a2 + 16a – 36 = 0
(a + 18) (a – 2) = 0  a = 2
(a = –18 scheidet aus, da es keine negativen Wahrscheinlichkeiten gibt.)
2.2 E(X) = 0·0,4·2 + 1·0,025·22 + 2·0,05 + 3·0,05 = 0,35
E(X2) = 0·0,4·2 + 1·0,025·22 + 4·0,05 + 9·0,05 = 0,75
Var(X) = E(X2) – (E(X))2 = 0,75 – 0,352 = 0,6275
a = 2
(a = –18 scheidet aus, da es keine negativen Wahrscheinlichkeiten gibt.)
2.2 E(X) = 0·0,4·2 + 1·0,025·22 + 2·0,05 + 3·0,05 = 0,35
E(X2) = 0·0,4·2 + 1·0,025·22 + 4·0,05 + 9·0,05 = 0,75
Var(X) = E(X2) – (E(X))2 = 0,75 – 0,352 = 0,6275  σ =
σ = 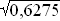 = 0,792
P(E(X)–2σ ≤ X ≤ E(X)+2σ) = P(–1,23 ≤ X ≤ 1,93)
= P(X = 0
= 0,792
P(E(X)–2σ ≤ X ≤ E(X)+2σ) = P(–1,23 ≤ X ≤ 1,93)
= P(X = 0 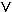 X = 1) = 0,8 + 0,1 = 0,9
2.3 p = P(X = 0) = 0,8 ; n = 200
X = 1) = 0,8 + 0,1 = 0,9
2.3 p = P(X = 0) = 0,8 ; n = 200  P(150 ≤ X ≤ 170) = F(170) – F(149) = 0,9717 – 0,0345 = 0,9372
2.4
P(150 ≤ X ≤ 170) = F(170) – F(149) = 0,9717 – 0,0345 = 0,9372
2.4 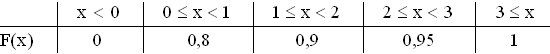 Graf der kumulativen Verteilungsfunktion F:
Graf der kumulativen Verteilungsfunktion F:
 k = 1 – F(2,3) = 1 – F(2) = 1 – 0,95 = 0,05 bedeutet die Wahrscheinlichkeit,
dass bei einer zufällig ausgewählten Briefmarke des neuen Drucks mehr als
zwei Fehler auftreten.
3.1 Var(X) = σ2 = n·p·q = n·p·(1–p)
k = 1 – F(2,3) = 1 – F(2) = 1 – 0,95 = 0,05 bedeutet die Wahrscheinlichkeit,
dass bei einer zufällig ausgewählten Briefmarke des neuen Drucks mehr als
zwei Fehler auftreten.
3.1 Var(X) = σ2 = n·p·q = n·p·(1–p)  8100 = 90000 (p – p2)
8100 = 90000 (p – p2)  0,09 = p – p2
0,09 = p – p2  p2 – p + 0,09 = 0 D = 1 – 0,36 = 0,64
p2 – p + 0,09 = 0 D = 1 – 0,36 = 0,64 
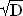 = 0,8
= 0,8  p1 / 2 = 0,5 ± 0,4
p1 / 2 = 0,5 ± 0,4  p1 = 0,9 ; p2 = 0,1
Gilt p = 0,1, dann werden insgesamt mehr fehlerfreie als fehlerhafte
Briefmarken gedruckt.
3.2 µ = n · p = 90000 · 0,1 = 9000
Mit 9000 fehlerhaften Marken ist zu rechnen.
4. Testgröße T: Anzahl der fehlerhaften Briefmarken in der Stichprobe der Länge 200.
Testart: einseitiger (rechtsseitiger) Signifikanztest
Nullhypothese H0: p = 0,05 (Gegenhypothese H1: p > 0,05)
Ablehnungsbereich: T1 = [k ; 200]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≥ k) < 0,01
p1 = 0,9 ; p2 = 0,1
Gilt p = 0,1, dann werden insgesamt mehr fehlerfreie als fehlerhafte
Briefmarken gedruckt.
3.2 µ = n · p = 90000 · 0,1 = 9000
Mit 9000 fehlerhaften Marken ist zu rechnen.
4. Testgröße T: Anzahl der fehlerhaften Briefmarken in der Stichprobe der Länge 200.
Testart: einseitiger (rechtsseitiger) Signifikanztest
Nullhypothese H0: p = 0,05 (Gegenhypothese H1: p > 0,05)
Ablehnungsbereich: T1 = [k ; 200]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≥ k) < 0,01  P(T ≤ k–1) > 0,99
k – 1 ≥ 18 (Tafelwerk)
k ≥ 19
P(T ≤ k–1) > 0,99
k – 1 ≥ 18 (Tafelwerk)
k ≥ 19  T1 = [19 ; 200]IN
Ab 19 fehlerhaften Briefmarken in der Stichprobe darf die Nullhypothese auf dem
1%-Niveau abgelehnt werden.
T1 = [19 ; 200]IN
Ab 19 fehlerhaften Briefmarken in der Stichprobe darf die Nullhypothese auf dem
1%-Niveau abgelehnt werden.
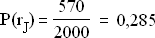
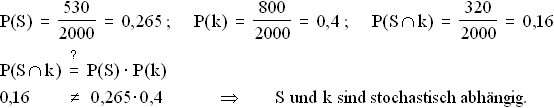 2.1 |Ω| = 5! = 120
2.2
2.1 |Ω| = 5! = 120
2.2 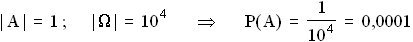 3.1 Es liegt eine Binomialverteilung mit n = 50 und p = 0,7 vor.
3.1 Es liegt eine Binomialverteilung mit n = 50 und p = 0,7 vor. 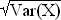 = 3,24
P(µ–σ ≤ X ≤ µ+σ) = P(31,76 ≤ X ≤ 38,24) = P(32 ≤ X ≤ 38)
= F(38) – F(31) = 0,861 – 0,141 = 0,72
3.2 Mindestens 15 PCs sind genau dann frei, wenn höchstens 35 PCs belegt sind.
P(X ≤ 35) = 0,553
4.1 Testart: einseitiger (linksseitiger) Signifikanztest (H0: p = 0,6 ; H1: p < 0,6)
Testgröße T: Anzahl der Internetnutzer aus der Stichprobe der Länge 200,
die über A surfen.
Ablehnungsbereich: T1 = [0 ; k]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≤ k) < 0,05
= 3,24
P(µ–σ ≤ X ≤ µ+σ) = P(31,76 ≤ X ≤ 38,24) = P(32 ≤ X ≤ 38)
= F(38) – F(31) = 0,861 – 0,141 = 0,72
3.2 Mindestens 15 PCs sind genau dann frei, wenn höchstens 35 PCs belegt sind.
P(X ≤ 35) = 0,553
4.1 Testart: einseitiger (linksseitiger) Signifikanztest (H0: p = 0,6 ; H1: p < 0,6)
Testgröße T: Anzahl der Internetnutzer aus der Stichprobe der Länge 200,
die über A surfen.
Ablehnungsbereich: T1 = [0 ; k]IN (0 ≤ k ≤ 200) mit der Eigenschaft:
P(T ≤ k) < 0,05 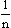
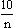
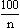
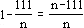
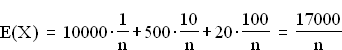 5.2
5.2 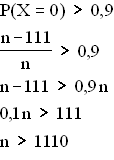 Ab n = 1111 Abonnenten wäre die Wahrscheinlichkeit, keinen Gewinn zu erzielen,
größer als 90%.
Ab n = 1111 Abonnenten wäre die Wahrscheinlichkeit, keinen Gewinn zu erzielen,
größer als 90%.