 1.2.1 A1 = {B
1.2.1 A1 = {B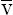 , E
, E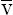 }
A2 = {FV, F
}
A2 = {FV, F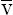 , EV, E
, EV, E }
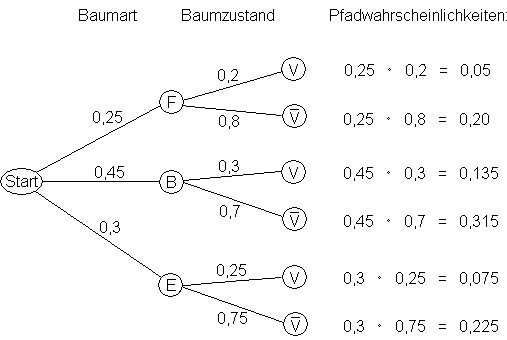
1.2.2 Untersuchung von A1 und A2 auf stochastische Unabhängigkeit:
P(A1
}
1.2.2 Untersuchung von A1 und A2 auf stochastische Unabhängigkeit:
P(A1  A2) = P({E
A2) = P({E }) = 0,225
P(A1) = 0,315 + 0,225 = 0,54 ; P(A2) = 0,25 + 0,3 = 0,55
P(A1) · P(A2) = 0,54 · 0,55 = 0,297 ≠ 0,225 = P(A1
}) = 0,225
P(A1) = 0,315 + 0,225 = 0,54 ; P(A2) = 0,25 + 0,3 = 0,55
P(A1) · P(A2) = 0,54 · 0,55 = 0,297 ≠ 0,225 = P(A1  A2)
A2)  A1 und A2 sind stochastisch abhängig.
1.3.1 Es liegt näherungsweise eine Binomialverteilung vor mit n = 20 und p = 0,25.
X = Anzahl der Fichten unter den ausgewählten Bäumen ;
P(X > 5) = 1 – P(X ≤ 5) = 1 – F(5) = 1 – 0,617 (s. Tafelwerk) = 0,383
1.3.2 p = P(„Laubbaum wird ausgewählt“) = 0,45 + 0,3 = 0,75 ; n = 20
A1 und A2 sind stochastisch abhängig.
1.3.1 Es liegt näherungsweise eine Binomialverteilung vor mit n = 20 und p = 0,25.
X = Anzahl der Fichten unter den ausgewählten Bäumen ;
P(X > 5) = 1 – P(X ≤ 5) = 1 – F(5) = 1 – 0,617 (s. Tafelwerk) = 0,383
1.3.2 p = P(„Laubbaum wird ausgewählt“) = 0,45 + 0,3 = 0,75 ; n = 20  µ = 20 · 0,75 = 15
X = Anzahl der Laubbäume unter den ausgewählten Bäumen ;
P(13 ≤ X ≤ 17) = F(17) – F(12) = (s. Tafelwerk) 0,909 – 0,102 = 0,807
1.4.1 Testgröße T = Anzahl der geschädigten Fichten unter den 200 ausgewählten Fichten
Nullhypothese: Schadensanteil liegt unverändert bei p = 0,2
(Rechtsseitiger) Ablehnungsbereich:
T1 = [51 ; 200]IN
WSK, mit der T im Ablehnungsbereich liegt:
P(T ≥ 51) = 1 – P(T ≤ 50) = 1 – F(50) = 1 – 0,9655 = 0,0345
1.4.2 In diesem Beispiel besteht der Fehler 2. Art darin, aufgrund des Testergebnisses irrtümlich
von einem unveränderten Schadensanteil auszugehen, obwohl er tatsächlich zugenommen hat.
2.1
µ = 20 · 0,75 = 15
X = Anzahl der Laubbäume unter den ausgewählten Bäumen ;
P(13 ≤ X ≤ 17) = F(17) – F(12) = (s. Tafelwerk) 0,909 – 0,102 = 0,807
1.4.1 Testgröße T = Anzahl der geschädigten Fichten unter den 200 ausgewählten Fichten
Nullhypothese: Schadensanteil liegt unverändert bei p = 0,2
(Rechtsseitiger) Ablehnungsbereich:
T1 = [51 ; 200]IN
WSK, mit der T im Ablehnungsbereich liegt:
P(T ≥ 51) = 1 – P(T ≤ 50) = 1 – F(50) = 1 – 0,9655 = 0,0345
1.4.2 In diesem Beispiel besteht der Fehler 2. Art darin, aufgrund des Testergebnisses irrtümlich
von einem unveränderten Schadensanteil auszugehen, obwohl er tatsächlich zugenommen hat.
2.1 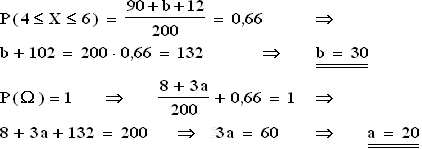 2.2.1 Wahrscheinlichkeitsverteilung von X :
2.2.1 Wahrscheinlichkeitsverteilung von X :
|
X = x |
1 |
2 |
3 |
4 |
5 |
6 |
|
P(X = x) |
8:200 = 0,04 |
20:200 = 0,1 |
40:200 = 0,2 |
90:200 = 0,45 |
30:200 = 0,15 |
12:200 = 0,06 |
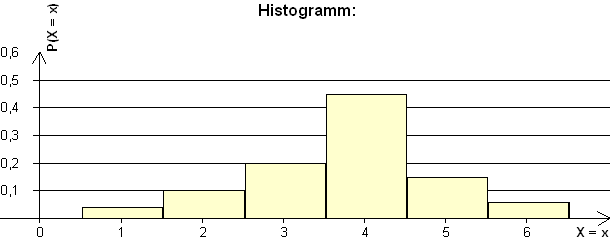 2.2.2 E(X) = 1·0,04 + 2·0,1 + 3·0,2 + 4·0,45 + 5·0,15 + 6·0,06 = 3,75
E(X2) = 1·0,04 + 4·0,1 + 9·0,2 + 16·0,45 + 25·0,15 + 36·0,06 = 15,35
Var(X) = E(X2) – (E(X))2 = 15,35 – 3,752 = 1,2875
2.2.2 E(X) = 1·0,04 + 2·0,1 + 3·0,2 + 4·0,45 + 5·0,15 + 6·0,06 = 3,75
E(X2) = 1·0,04 + 4·0,1 + 9·0,2 + 16·0,45 + 25·0,15 + 36·0,06 = 15,35
Var(X) = E(X2) – (E(X))2 = 15,35 – 3,752 = 1,2875  σ =
σ = 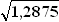 = 1,135
P(E(X)–σ ≤ X ≤ E(X)+σ) = P(2,615 ≤ X ≤ 4,885)
= P(X = 3
= 1,135
P(E(X)–σ ≤ X ≤ E(X)+σ) = P(2,615 ≤ X ≤ 4,885)
= P(X = 3 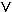 X = 4) = 0,2 + 0,45 = 0,65
X = 4) = 0,2 + 0,45 = 0,65
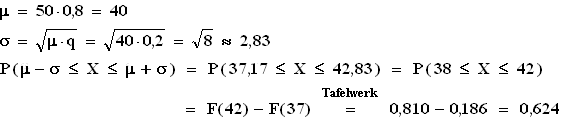 2.1 Testgröße T: Anzahl der guten Kopien unter 50 Kopien mit Gerät H.
Art des Tests: linksseitiger Signifikanztest
Nullhypothese H0: „Die Kopierqualität ist gleich geblieben.“ Also: p = 0,9
Max. Ablehnungsbereich von H0: T1 = [ 0 ; 42 ]Z
2.2 P(T ≤ 42) = F(42) = 0,122 (Tafelwerk)
Der Fehler 1. Art kann entweder durch eine Verkleinerung des Ablehnungsbereiches
oder (bei proportional gleichbleibendem Ablehnungsbereich) durch eine Vergrößerung
der Stichprobenlänge erreicht werden.
2.3 Sei r der Rückweisungspunkt. Dann soll gelten :
P(T ≤ r) ≤ 0,02
Aus dem Tafelwerk geht r = 39 hervor.
2.1 Testgröße T: Anzahl der guten Kopien unter 50 Kopien mit Gerät H.
Art des Tests: linksseitiger Signifikanztest
Nullhypothese H0: „Die Kopierqualität ist gleich geblieben.“ Also: p = 0,9
Max. Ablehnungsbereich von H0: T1 = [ 0 ; 42 ]Z
2.2 P(T ≤ 42) = F(42) = 0,122 (Tafelwerk)
Der Fehler 1. Art kann entweder durch eine Verkleinerung des Ablehnungsbereiches
oder (bei proportional gleichbleibendem Ablehnungsbereich) durch eine Vergrößerung
der Stichprobenlänge erreicht werden.
2.3 Sei r der Rückweisungspunkt. Dann soll gelten :
P(T ≤ r) ≤ 0,02
Aus dem Tafelwerk geht r = 39 hervor. 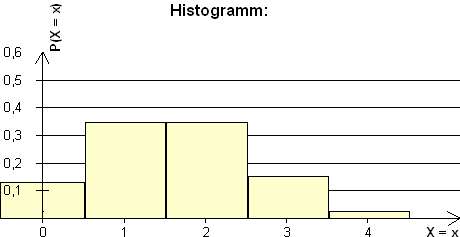 3.2 Kumulative Verteilungsfunktion F:
3.2 Kumulative Verteilungsfunktion F:
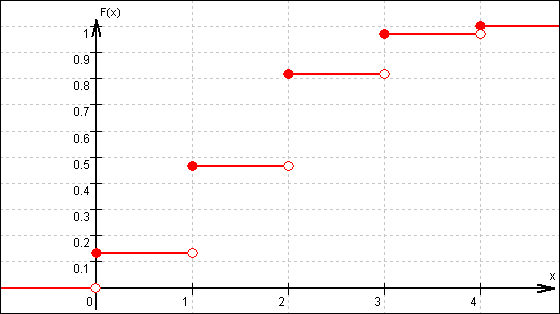 3.3 P(2 ≤ X ≤ 3) = 0,3456 + 0,1536 = 0,4992
4.1 Um mindestens 8000
3.3 P(2 ≤ X ≤ 3) = 0,3456 + 0,1536 = 0,4992
4.1 Um mindestens 8000  Mehreinnahmen zu erzielen, müsste der Händler mindestens
100 Geräte des Typs H haben.
Es liegt eine B(200; 0,6)-verteilte Zufallsgröße vor :
P(X ≥ 100) = 1 – P(X ≤ 99) = 1 – F(99) = 1 – 0,00168 = 0,99832
4.2 Erwartungswert für die Anzahl der Geräte des Typs H: µ = 200·0,6 = 120
Mehreinnahmen zu erzielen, müsste der Händler mindestens
100 Geräte des Typs H haben.
Es liegt eine B(200; 0,6)-verteilte Zufallsgröße vor :
P(X ≥ 100) = 1 – P(X ≤ 99) = 1 – F(99) = 1 – 0,00168 = 0,99832
4.2 Erwartungswert für die Anzahl der Geräte des Typs H: µ = 200·0,6 = 120