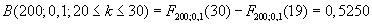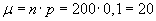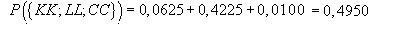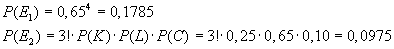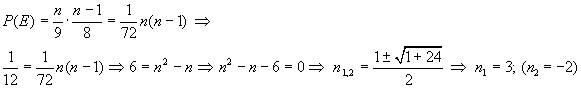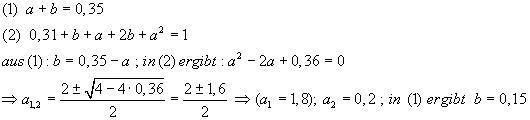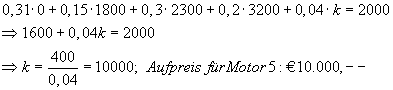1.0
A: Bauteil A ist einwandfrei
B: Bauteil B ist einwandfrei
C: Bauteil C ist einwandfrei
![]() :
Bauteil A ist fehlerhaft
:
Bauteil A ist fehlerhaft
![]() :
Bauteil B ist fehlerhaft
:
Bauteil B ist fehlerhaft
![]() :
Bauteil C ist fehlerhaft
:
Bauteil C ist fehlerhaft
Die Wahrscheinlichkeit, dass das Bauteil A einwandfrei
ist, beträgt P(A) = a .
Die Wahrscheinlichkeit, dass das Bauteil A fehlerhaft ist, beträgt ![]() .
.
Analog gilt P(B)= 0,9 , ![]()
und P(C)=0,8 , ![]() .
.
Behauptung: Alle drei Bauteile arbeiten einwandfrei mit einer Wahrscheinlichkeit
von 0,612, wenn a = 0,85
Diese Behauptung ist zu zeigen:
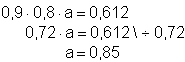
Da P(A) = 0,85 ist, gilt die Behauptung
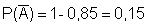
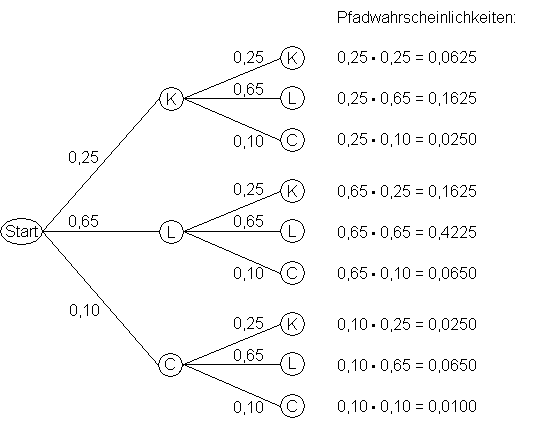
Baumdiagramm :
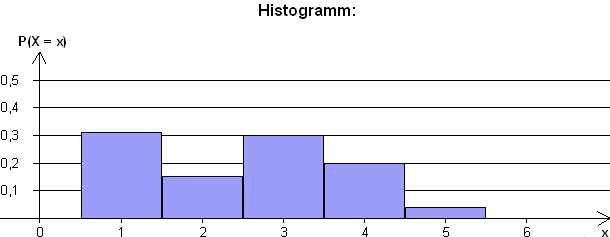
Wertetabelle der Bionominalverteilung :
P(X=1) = 0,017 + 0,027 + 0,012 = 0,056
P(X=2) = 0,153 + 0,068 + 0,108 = 0,329
![]()
Wertetabelle der kumulativen Verteilungsfunktion
F :
![]()
Die kumulative Verteilungsfunktion F :
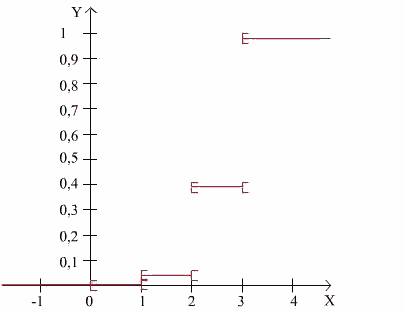
P = 1 - F(1,5)
P = 1 - 0,059 = 0,941
Interpretation: 0,941 ist die Wahrscheinlichkeit dafür,
dass mindestens zwei Bauteile während eines Tages einwandfrei arbeiten.
![]() :
" Die Maschine fällt nur am 4. Arbeitstag aus."
:
" Die Maschine fällt nur am 4. Arbeitstag aus."
Berechnung der Wahrscheinlichkeit, indem man sich einen Teil dieses
Baumdiagramms vorstellt.
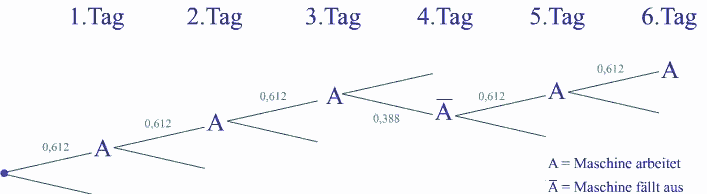
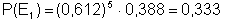
![]() "
Die Maschine fällt an genau 2 Tagen aus"
"
Die Maschine fällt an genau 2 Tagen aus"
Berechnung der Wahrscheinlichkeit des Ereignis mit der Formel der Bernoulli-Kette.
![]()
Ereignis M: Kunststoffgehäuse hat einen Materialfehler
Ereignis F: Kunststoffgehäuse hat einen nicht akzeptierbare Formabweichung
Die Wahrscheinlichkeit, dass das Ereignis M eintritt, beträgt P(M)
= 0,08
Die Wahrscheinichkeit, dass das Ereignis F eintritt, beträgt P(F)
= 0,05
Formel der stochastischen Unabhängigkeit :
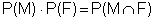
Diese wird nun überprüft :
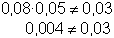
Damit gelten die Ereignisse M und F als stochastisch abhängig.
![]() :
Das Gehäuse hat einen Materialfehler oder eine nicht abkzeptierbare
Formabweichung, d. h. es ist fehlerhaft.
:
Das Gehäuse hat einen Materialfehler oder eine nicht abkzeptierbare
Formabweichung, d. h. es ist fehlerhaft.
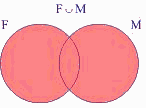
Vierfeldertafel:

Ablesen aus der Vierfeldertafel
![]()
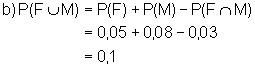
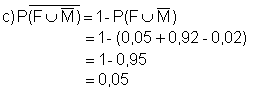 oder:
oder:![]()
Nullhypothese: "mindestens 10% der Gehäuse sind
fehlerhaft"![]()
Gegenhypothese: "weniger als 10% der Gehäuse sind fehlerhaft"![]()
Testgröße: Anzahl der fehlerhaften Gehäuse
Es ist ein einseitiger Signifikanztest

Ablesen in der Zeichnung: Linksseitiger Test
Berechnung des größtmöglichen Ablehnungsbereichs der Nullhypothese
für den Fehler 1. Art![]()
n = 200 p = 0,1
Signifikanzniveau
![]()
![]() (siehe Tafelwerk - rechte Spalte!), also k =11
(siehe Tafelwerk - rechte Spalte!), also k =11
![]()