Prüfung zur Erlangung der Fachhochschulreife
2005
SI: Lösungen
| 1.1 |
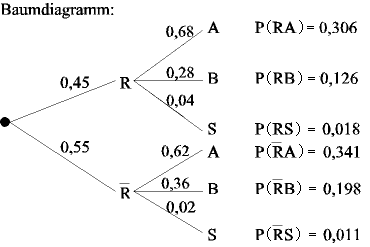 |
| |
|
| 1.2 |
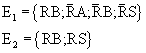 |
| |
|
| 2.1 |
 |
| |
|
| |
|
| |
|
| 2.2 |
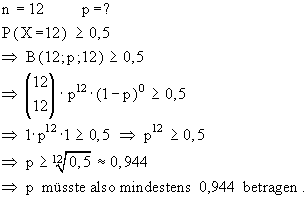 |
| |
|
| 3.1 |
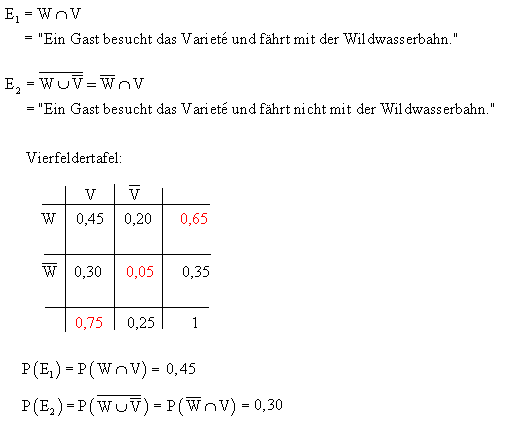 |
| |
|
| 3.2 |
 |
| |
|
| 4. |
 |
| |
|
| 5.1 |
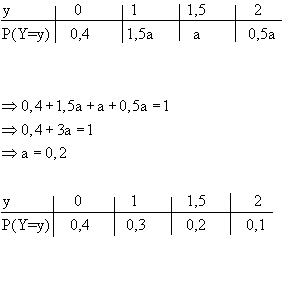 |
| |
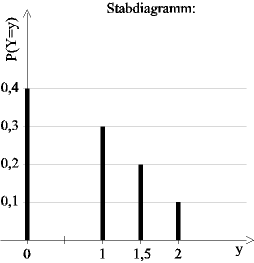 |
| |
|
| 5.2 |
 |
| |
|
| 6. |
 |
S II: Lösungen
- 1.1
- Baumdiagramm:
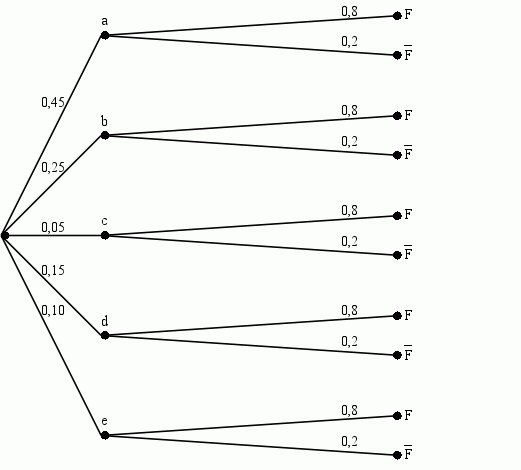
Pfadwahrscheinlichkeiten:
| ω | aF | aF | bF | bF | cF | cF | dF | dF | eF | eF |
| P({ω}) | 0,45 · 0,8 = 0,36 | 0,45 · 0,2 = 0,09 | 0,25 · 0,8 = 0,20 | 0,25 · 0,2 = 0,05 | 0,05 · 0,8 = 0,04 | 0,05 · 0,2 = 0,01 | 0,15 · 0,8 = 0,12 | 0,15 · 0,2 = 0,03 | 0,1 · 0.8 = 0,08 | 0,1 · 0,2 = 0,02 |
- 1.2.1
- Wahrscheinlichkeitsverteilung:
P(15) = P({aF}) = 0,36
P(25) = P({aF}) + P({bF}) = 0,09 + 0,20 = 0,29
P(35) = P({bF}) + P({cF}) = 0,05 + 0,04 = 0,09
P(45) = P({cF}) = 0,01
P(50) = P({dF}) = 0,12
P(60) = P({dF}) + P({eF}) = 0,03 + 0,08 = 0,11
P(70) = P({eF}) = 0,02
| x | 15 | 25 | 35 | 45 | 50 | 60 | 70 |
| P(X=x) | 0,36 | 0,29 | 0,09 | 0,01 | 0,12 | 0,11 | 0,02 |
- 1.2.2
- P(X≥40) = P(45) + P(50) + P(60) + P(70) = 0,01 + 0,12 + 0,11 + 0,02 = 0,26
- 1.2.3
- E(X) = 15·0,36 + 25·0,29 + 35·0,09 + 45·0,01 + 50·0,12 + 60·0,11 + 70·0,02
= 5,40 + 7,25 + 3,15 + 0,45 + 6,00 + 6,60 + 1,40 = 30,25 €
- 1.2.4
- P(E) = P(15<X ≤50) =
= P(25) + P(35) + P(45) + P(50) =
= 0,29 + 0,09 + 0,01 + 0,12 =
= 0,51
E: Der fällige Betrag ist mindestens 25 €, höchstens 50 €.
- 2.1
- p = 0,1
n = 200
X = Anzahl der Fahrer mit überhöhter Geschwindigkeit
P(X>0,12·200) = P(X>24) = 1 - (X ≤24) = 1 - 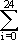 B(200;0,1;i) = 1 - 0,85511 = 0,14489
B(200;0,1;i) = 1 - 0,85511 = 0,14489
µ = n · p  µ = 200 · 0,1 = 20
µ = 200 · 0,1 = 20
σ = √n · p · q  σ = √200 · 0,1 · 0,9 = 4,243
σ = √200 · 0,1 · 0,9 = 4,243
µ + σ = 20 + 4,243 = 24,243
24,243<25  Behauptung
Behauptung
- 2.2
- Einnahmen in den ersten 30 Tagen: µ · 28 · 30 = 20 · 28 · 30 = 16800 €
Tageseinnahmen anschließend: 0,5 · µ · 28 = 280 €
(60000 - 16800) : 280 = 154,3  154,3 + 30 = 184,3
154,3 + 30 = 184,3  Kosten sind nach 185 Tagen gedeckt
Kosten sind nach 185 Tagen gedeckt
- 2.3
- Testgröße T: Anzahl der Temposünder unter 200 Kontrollierten
H0:p ≤0,02; H1:p>0,02
Annahmebereich von H0:[0;c - 1]N
Ablehnungsbereich von H0:[c;200]N
P(T≥c) ≤ 0,05  1 - P(T ≤c - 1) ≤ 0,05
1 - P(T ≤c - 1) ≤ 0,05  P(T ≤c - 1)≥0,95
P(T ≤c - 1)≥0,95 
 B(200;0,02;i)≥0,95
B(200;0,02;i)≥0,95  c - 1≥7
c - 1≥7  c = 8
c = 8
 Max. Ablehnungsbereich von H0:[8;200]N
Max. Ablehnungsbereich von H0:[8;200]N
- 3.1
- Vierfeldertafel:
| | F | F | |
| S | 0,04 | 0,06 | 0,1 |
| S | 0,76 | 0,14 | 0,9 |
| | 0,8 | 0,2 | 1 |
P(F) · P(S) = 0,8 · 0,9 = 0,72
P(F S) = 0,76
S) = 0,76
 P(F) · P(S) ≠ P(F
P(F) · P(S) ≠ P(F S)
S)  F und S sind stochastisch abhängig.
F und S sind stochastisch abhängig.
- 3.2
- F
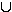 S : "Der Fahrer hat seine Papiere dabei oder ist zu schnell gefahren oder beides"
S : "Der Fahrer hat seine Papiere dabei oder ist zu schnell gefahren oder beides"
P(F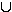 S) = 1 - 0,14 = 0,86
S) = 1 - 0,14 = 0,86

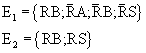

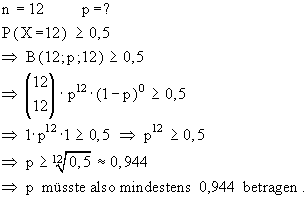
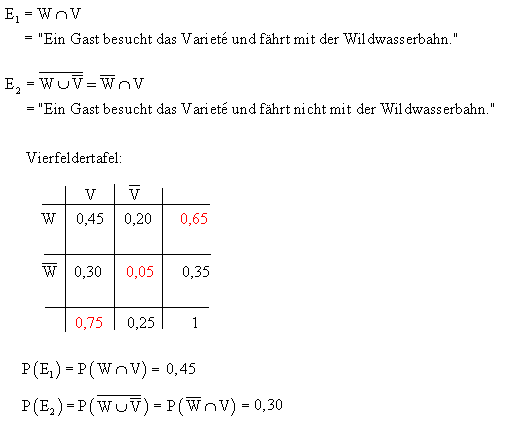


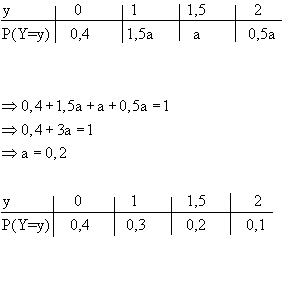




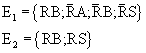

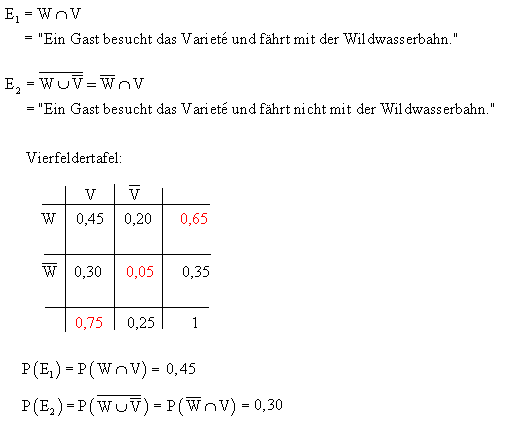


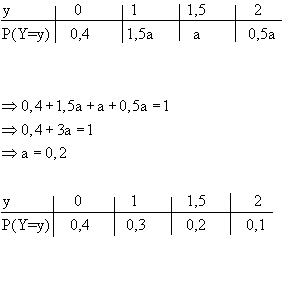




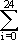 B(200;0,1;i) = 1 - 0,85511 = 0,14489
B(200;0,1;i) = 1 - 0,85511 = 0,14489 µ = 200 · 0,1 = 20
µ = 200 · 0,1 = 20 σ = √200 · 0,1 · 0,9 = 4,243
σ = √200 · 0,1 · 0,9 = 4,243 Behauptung
Behauptung 154,3 + 30 = 184,3
154,3 + 30 = 184,3  Kosten sind nach 185 Tagen gedeckt
Kosten sind nach 185 Tagen gedeckt 1 - P(T ≤c - 1) ≤ 0,05
1 - P(T ≤c - 1) ≤ 0,05  P(T ≤c - 1)≥0,95
P(T ≤c - 1)≥0,95 
 B(200;0,02;i)≥0,95
B(200;0,02;i)≥0,95  c - 1≥7
c - 1≥7  c = 8
c = 8 Max. Ablehnungsbereich von H0:[8;200]N
Max. Ablehnungsbereich von H0:[8;200]N  S) = 0,76
S) = 0,76 P(F) · P(S) ≠ P(F
P(F) · P(S) ≠ P(F S)
S)  F und S sind stochastisch abhängig.
F und S sind stochastisch abhängig. 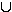 S : "Der Fahrer hat seine Papiere dabei oder ist zu schnell gefahren oder beides"
S : "Der Fahrer hat seine Papiere dabei oder ist zu schnell gefahren oder beides" S) = 1 - 0,14 = 0,86
S) = 1 - 0,14 = 0,86