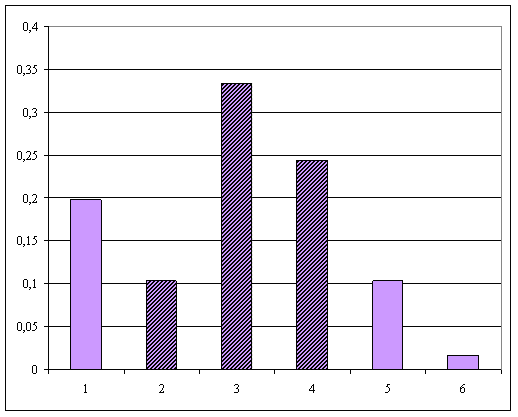
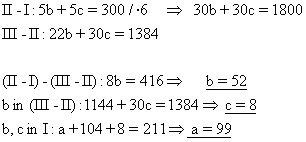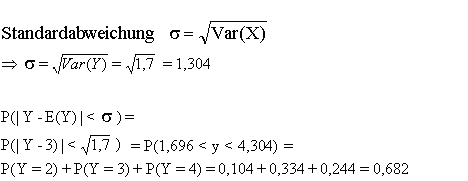1.
|
Laplace- Formel :
P(A) = 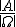
A: Anzahl der günstigen Ergebnisse= 812000 verloste Tickets
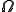 : Anzahl der möglichen Ergebnisse= 8,1 Millionen bestellte Tickets : Anzahl der möglichen Ergebnisse= 8,1 Millionen bestellte Tickets
Wahrscheinlichkeit, in genau einem Versuch ein Ticket zu erwerben:
P = 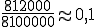
Bernoullische Formel: B(n;p;k) = 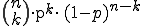
p = 0,1; n =16
a) P(a) = 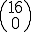 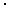 0,10 0,10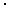 0,916 = 1 0,916 = 1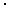 1 1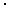 0,916 = 0,185 0,916 = 0,185
b) P(X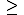 1) = 1- P(a) = 0,815 1) = 1- P(a) = 0,815
c) P(c) = 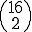  0,12 0,12 0,914 = 0,275 0,914 = 0,275
d)
Diese Aufgabe ist nicht lösbar. Man könnte sich vorstellen, es gäbe nur das Eröffnungsspiel und das Finale (woher soll ein Fußball-Laie denn wissen, dass dem nicht so ist?), und die Wahrscheinlichkeit, eine Karte zu bekommen, wäre für jedes der beiden Spiele gleich gross. Dann betrüge die Wahrscheinlichkeit, bei 16 Versuchen für jedes der beiden Spiele genau eine Karte zu bekommen, P(c) 0,5 = 0,1375. Tatsächlich gibt es jedoch zwischen dem Eröffnungsspiel und dem Finale viele weitere Spiele, so dass also die besagte Wahrscheinlichkeit viel kleiner ist und sich nicht ohne Kenntnis der Anzahl der Spiele berechnen lässt. 0,5 = 0,1375. Tatsächlich gibt es jedoch zwischen dem Eröffnungsspiel und dem Finale viele weitere Spiele, so dass also die besagte Wahrscheinlichkeit viel kleiner ist und sich nicht ohne Kenntnis der Anzahl der Spiele berechnen lässt.
|
|
| |
|
| 2.1 |
Baumdiagramm:
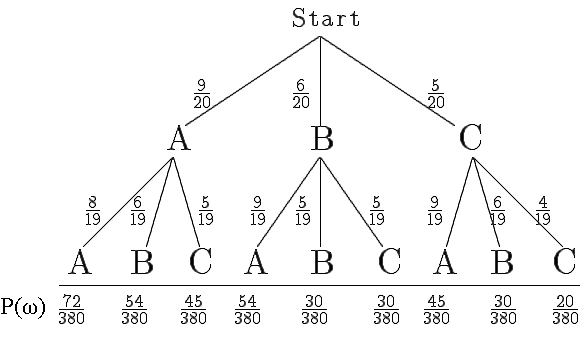 |
| 2.2 |
Für Rosi und Sven ist die WSK, dass sie im selben Block Karten erhalten, wie folgt:
P("Rosi und Sven") = P(AA) + P(BB) + P(CC) = 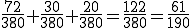 |
|
|
| 3.1 |
Vierfeldertafel:
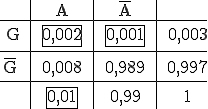
markierte Felder: Werte sind gegeben;
P(E1) = 0,008; P(E2) = 0,997 |
| |
|
3.2 |
Stochastische (Un-)abhängigkeit :
P(A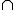 G) = P(A) G) = P(A)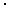 P(G) P(G)
0,002 = 0,01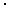 0,003 0,003
0,002 >
0,00003 , d. h. A und G sind stochastisch abhängig (sie begünstigen sich gegenseitig). |
| |
|
| 3.3 |
Satz von Sylvester :
P(A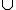 G) = P(A) + P(G) – P(A G) = P(A) + P(G) – P(A G) = 0,01 + 0,003 – 0,002 = 0,011 G) = 0,01 + 0,003 – 0,002 = 0,011 |
| |
|
| 3.4.1 |
Bernoullische Formel; p = 0,01; n = 200 ( siehe Tafelwerk)
P(X 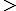 5) = 1 – F(5 ) = 1 – 0,98398 = 0,01602 5) = 1 – F(5 ) = 1 – 0,98398 = 0,01602 |
| |
|
| 3.4.2 |
Erwartungswert: 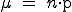 = 200 = 200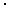 0,01 = 2 0,01 = 2
Standardabweichung: 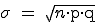 = 1,41 = 1,41
P(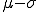 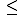 X X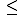 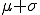 ) = P(0,59 ) = P(0,59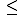 X X 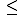 3,41) = P(1 3,41) = P(1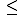 X X 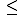 3) = F(3) – F(0) = 3) = F(3) – F(0) =
0,85803 – 0,13398 = 0,72405 |
|
|
| 4.1 |
p = 0,7 (dass das Tor fällt); n = 8; (Tafelwerk)
X:"Anzahl der gefallenen Tore."
P(X 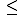 3) = F(3) = 0,05797 3) = F(3) = 0,05797 |
| |
|
| 4.2 |
Rechtsseitiger Signifikanztest
H0: p ≤ 0,3; H1: p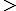 0,3 0,3
T: "Anzahl der abgewehrten Elfmeter in der Stichprobe."
n = 100;
P(T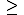 r) r)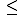 0,05 0,05
Gegenereignis: P(T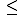 r – 1) r – 1)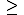 0,95 (siehe Tafelwerk) 0,95 (siehe Tafelwerk)
r – 1 ≥ 38
r ≥ 39
Daraus ergibt sich:
Annahmebereich: 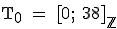 ; Ablehnungsbereich: ; Ablehnungsbereich: 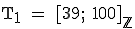
Der Trainer wird die Behauptung des Ersatztorwarts ablehnen, da 35 im Annahmebereich liegt. |
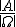


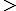 5) = 1 – F(5 ) = 1 – 0,98398 = 0,01602
5) = 1 – F(5 ) = 1 – 0,98398 = 0,01602 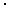 0,01 = 2
0,01 = 2 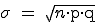
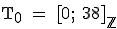 ; Ablehnungsbereich:
; Ablehnungsbereich: 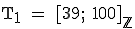
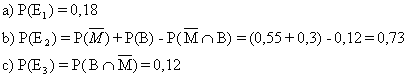
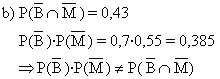
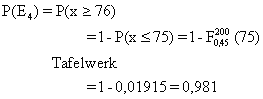
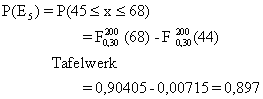
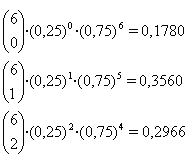 etc.
etc.