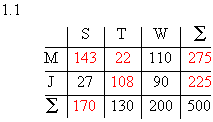
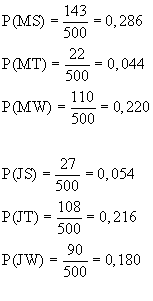
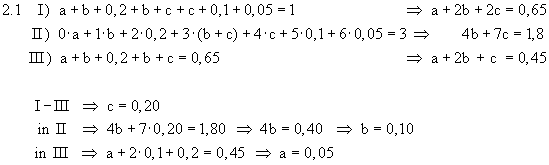
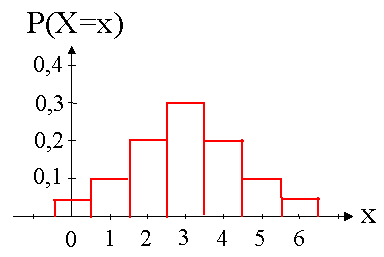
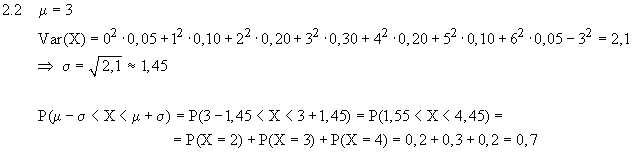
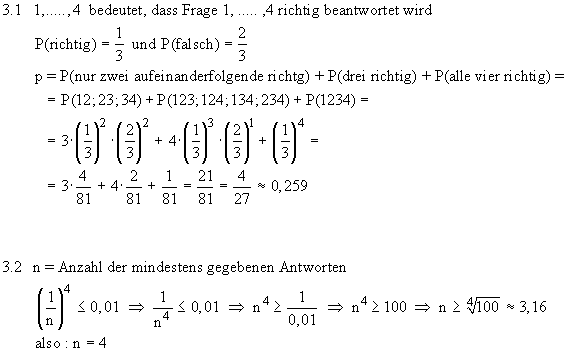
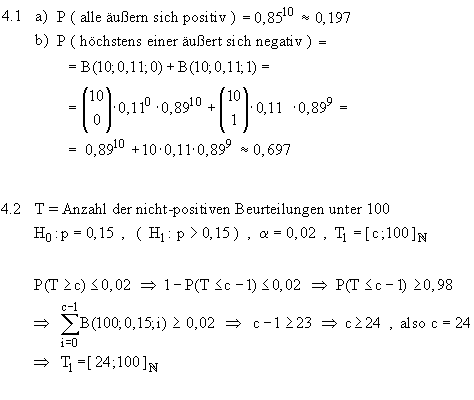
Abschlussprüfung zur Erlangung der Fachhochschulreife
Frühjahr 2007

S I:   Lösungen

S II:   Lösungen

1.1	
1.2	P(E1) = P(b)·P(h) = 0,7·0,6 = 0,42
	P(E2) = 1 – P(n) = 1 – 0,1 = 0,9


1.3	E3 = {snG; smG; shG; bnG; bmG; bhG}
	P(E3) = 0,021 + 0,063 + 0,108 + 0,049 + 0,147 + 0,252 = 0,64




2.1	Testgröße T: Anzahl der defekten Scharniere in der Stichprobe von 50 Scharnieren
	Nullhypothese H0: p ≤ 0,02
	P(T ≥ 3) = 1 – P(T ≤ 2) = 1 – 0,92157(Tafelwerk: p = 0,02; n=50; P(T ≤ 2)) = 0,07843


2.2	P(T ≥ k) ≤ 0,05
	P(T ≤ k–1) ≥ 0,95
	k–1 ≥ 3
	k ≥ 4
	Maximaler Ablehnungsbereich T1 = { 4 ; . . . ; 50 }


2.3	Bei diesem Beispiel besteht der Fehler 2. Art darin, dass man aufgrund des Stichproben-
	ergebnisses annimmt, in der Lieferung seien höchstens 2% der Scharniere defekt,
	obwohl der Prozentsatz der defekten Scharniere in Wirklichkeit höher ist.




3.1	


3.2	
	Also sind die Ereignisse  und G stochastisch (negativ) voneinander abhängig.




4.1	p = 0,1;  n = 100

	a)	P(X < 3) = F(2) = 0,00194

	b)	

	c)	P("1. und 2. Türgriff defekt") = 0,1 · 0,1 = 0,01


4.2	Wahrscheinlichkeit, dass die Stichprobe von 100 Türgriffen weniger
	als 10 defekte Türgriffe enthält:
	P(X < 10) = F(9) = 0,45129