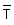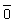Frühjahr 2008
Aufgabengruppe S I Musterlösung
Allgemeine Vorbemerkung:
Die Musterlösung wurde im Rahmen einer Seminararbeit von Marc Boujong erstellt.
| 1.1 | 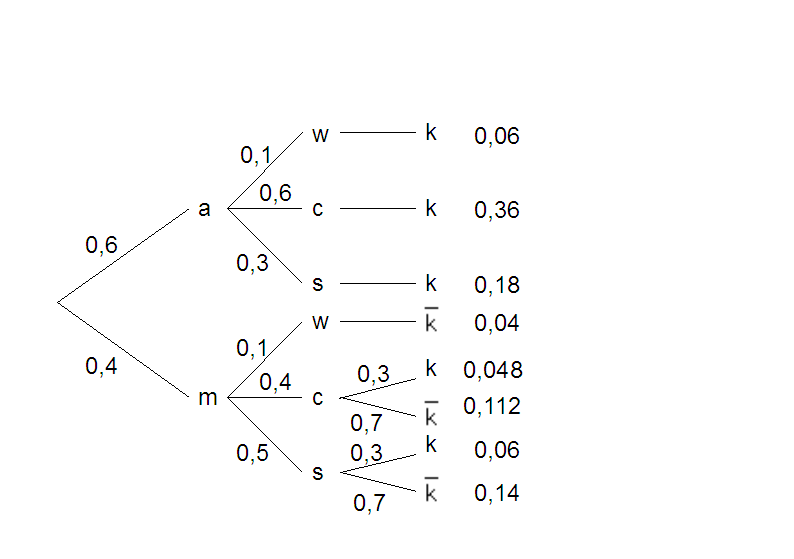
(6 BE) | ||||||||||||||||
| 1.2 | Zu diesem Zufallsexperiment gibt es mehr als zwei Ergebnisräume. In jeder Lösung müssen alle Ergebnisse des Zufallsexperiments enthalten sein: 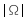 =3 =3
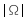 =2 =2
(2 BE) | ||||||||||||||||
| 1.3 |
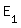 ={ask; msk; ms ={ask; msk; ms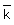 ; mw ; mw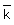 ; mc ; mc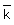 } }P( 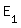 ) = 0,6 * 0,3 + 0.4 * 0,5 * 0,3 + 0,4 * 0,5 * 0,7 + 0,4 * 0,1 + 0,4 * 0,4 * 0,7 = 0,532 ) = 0,6 * 0,3 + 0.4 * 0,5 * 0,3 + 0,4 * 0,5 * 0,7 + 0,4 * 0,1 + 0,4 * 0,4 * 0,7 = 0,532(2 BE) |
||||||||||||||||
| 1.4 | Folgende
Ereignisse sind vorgegeben: A: „Ein Getränk wird am Automaten gekauft.“ S: „Es wird eine Flasche Saft gekauft.“ K: „Das gekaufte Getränk ist gekühlt.“ 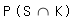 Saft wird gekauft und ist gekühlt 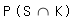 = 0,6 * 0,3 + 0,4 * 0,5 * 0,3 = 0,24 = 0,6 * 0,3 + 0,4 * 0,5 * 0,3 = 0,24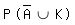 Getränk wird bei Max gekauft oder ist gekühlt 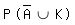 = = 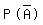 + + 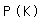 - - 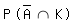 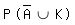 = 0,4 + 0,708 - 0,108 = 1 = 0,4 + 0,708 - 0,108 = 1
alternativ: A ist in K enthalten, also gilt (4 BE) |
| 2 |
P(T)= 40/50 = 0,8 P(O)= 25/50 = 0,5 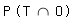 = 20/50 = 0,4 = 20/50 = 0,4
P(T)*P(O) = 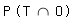 0,8*0.5 = 0,4 d.h. stochastisch unabhängig (5 BE) |
| 3.1 | Die
Zufallsgröße X gibt die Anzahl der Tassen Tee an, die ein Gast bei einem Frühstück trinkt. Es ergibt sich folgende Verteilung:
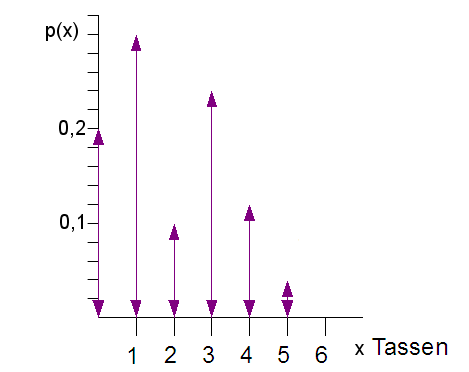 Erwartungswert: E (X) = 1*P(15)+2*P(5)+3*P(12)+4*P(6)+5*P(2) = 1,9 |
||||||
| 3.2 | P(X 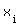 ) ) 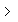 90% 90%Laut 3.1: P(X 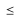 4) = 1 - 0,04 = 0.96 4) = 1 - 0,04 = 0.96Lösung: vier Tassen je Gast! (3 BE) |
| 4.1 | Bestimmen
Sie die Wahrscheinlichkeiten folgender Ereignisse: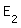 : „Von 50 Gästen wählen mehr als 3 das
vegetarische Gericht.“ : „Von 50 Gästen wählen mehr als 3 das
vegetarische Gericht.“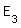 : „Die Zahl der vegetarischen Essen bei 100
Gästen liegt innerhalb der : „Die Zahl der vegetarischen Essen bei 100
Gästen liegt innerhalb der einfachen Standardabweichung um den Erwartungswert.“ 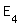 : „Von 100 Gästen essen 99 nicht das
vegetarische Gericht.“ : „Von 100 Gästen essen 99 nicht das
vegetarische Gericht.“Benötigtes Hilfsmittel: Tafelwerk der Stochastik P( 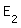 ) = P(X ) = P(X 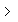 3) = 1 - P(X 3) = 1 - P(X 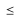 3) 1- 3) 1- 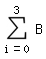 (50, 0,03, i) = 1- F(3) (50, 0,03, i) = 1- F(3)P( 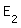 ) = 0.06276 ) = 0.06276
P( 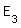 ) = P(1,29 ) = P(1,29 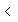 X X 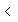 4,71) = F(4) - F(1) = 4,71) = F(4) - F(1) = 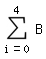 (100, 0,03, i) - (100, 0,03, i) - 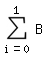 (100, 0,03, i) (100, 0,03, i)P( 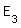 ) = 0,62323 ) = 0,62323
P( 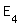 ) = P(X = 1) = W(1) = B (100, 0,03, 1) ) = P(X = 1) = W(1) = B (100, 0,03, 1)P( 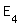 ) = 0,14707 ) = 0,14707
(8 BE) |
| 4.2 | Testgröße: X = Anzahl vegetarischer Essen n = 200 Nullhypothese: 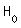 : p : p 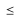 0,03 0,03Gegenhypothese: 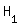 : p : p 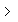 0,03 0,03Annahmebereich: A = {0, 1, ..., k} Ablehnungsbereich: L = {k+1, ..., 200} Signifikanzniveau: 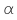 = 0,05 = 0,05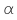 = P(L) = P(L) 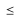 0,05 0,051-P(A) 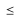 0,05 0,05P(A) 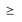 0,95 0,95 Laut Tafelwerk: 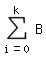 (200, 0,03, i) = 0,95987 für
k = 10 (200, 0,03, i) = 0,95987 für
k = 10also L = {11, ..., 200} Fehler 1. Art: 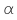 = 1 - 0,95987 = 0,04013 = 1 - 0,95987 = 0,04013
(6 BE) |