Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 1999
S I: Lösungen
1. 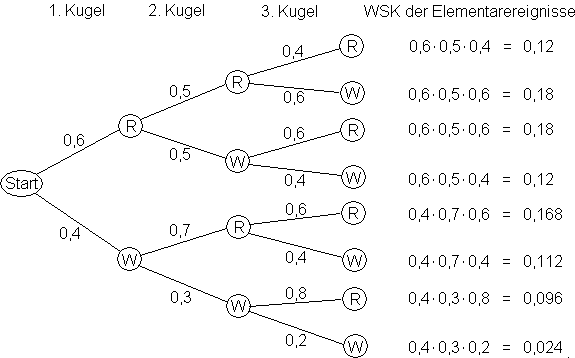 2.1 P(A) = P({RRR, WWW}) = 0,12 + 0,024 = 0,144
P(B) = P({RRR, RRW, RWR, WRR}) = 0,12 + 0,18 + 0,18 + 0,168 = 0,648
Untersuchung von A und B auf stoch. Unabhängigkeit:
P(A
2.1 P(A) = P({RRR, WWW}) = 0,12 + 0,024 = 0,144
P(B) = P({RRR, RRW, RWR, WRR}) = 0,12 + 0,18 + 0,18 + 0,168 = 0,648
Untersuchung von A und B auf stoch. Unabhängigkeit:
P(A  B) = P({RRR}) = 0,12
P(A) · P(B) = 0,144 · 0,648 = 0,093312 ≠ 0,12 = P(A
B) = P({RRR}) = 0,12
P(A) · P(B) = 0,144 · 0,648 = 0,093312 ≠ 0,12 = P(A  B)
B)  A und B sind stochastisch abhängig.
2.2
A und B sind stochastisch abhängig.
2.2 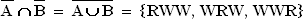 Es handelt sich um das Ereignis: „Es wird genau eine rote Kugel gezogen.“
P(
Es handelt sich um das Ereignis: „Es wird genau eine rote Kugel gezogen.“
P(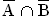 ) = 0,12 + 0,112 + 0,096 = 0,328
2.3
) = 0,12 + 0,112 + 0,096 = 0,328
2.3 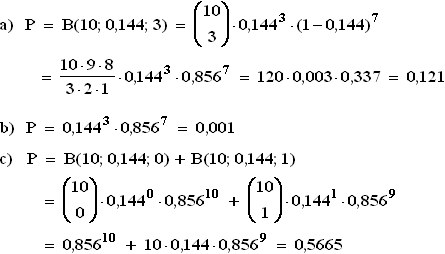 3.1
3.1 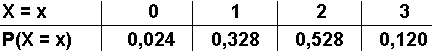 (Alle Werte sind dem Baumdiagramm von Aufgabe 1 entnommen.)
3.2
(Alle Werte sind dem Baumdiagramm von Aufgabe 1 entnommen.)
3.2 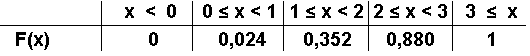 Graf der kumulativen Verteilungsfunktion F:
Graf der kumulativen Verteilungsfunktion F:
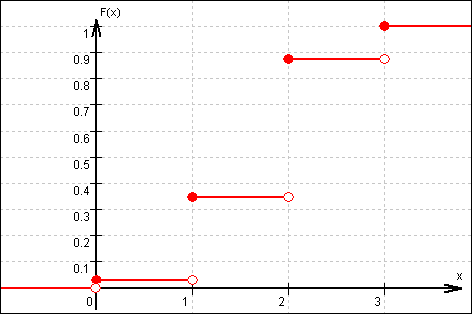 4.1 Das Spiel ist fair, wenn E(X) = 0.
4.1 Das Spiel ist fair, wenn E(X) = 0.  a · 0,024 + 3 · 0,328 – 2 · 0,528 – 5 · 0,120 = 0
0,024 a = 0,672
a = 28
4.2
a · 0,024 + 3 · 0,328 – 2 · 0,528 – 5 · 0,120 = 0
0,024 a = 0,672
a = 28
4.2 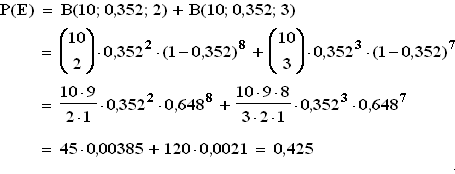
 P(
P(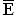 ) = 1 – 0,425 = 0,575 > P(E).
Also ist es günstiger, auf das Ereignis
) = 1 – 0,425 = 0,575 > P(E).
Also ist es günstiger, auf das Ereignis 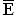 zu setzen.
5. Gegenhypothese: p ≠ 0,45
Linksseitiger Ablehnungsbereich:
T1 links = [0 ; kl]IN
Also gilt für T Gewinne:
P(T ≤ kl) < 0,005
kl ≤ 31 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
zu setzen.
5. Gegenhypothese: p ≠ 0,45
Linksseitiger Ablehnungsbereich:
T1 links = [0 ; kl]IN
Also gilt für T Gewinne:
P(T ≤ kl) < 0,005
kl ≤ 31 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
 T1 links = [0 ; 31]IN
Rechtsseitiger Ablehnungsbereich:
T1 rechts = [kr ; 100]IN
Also gilt für T Gewinne:
P(T ≥ kr) < 0,005
P(T ≤ kr–1) > 0,995
kr–1 ≥ 58 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
kr ≥ 59
T1 links = [0 ; 31]IN
Rechtsseitiger Ablehnungsbereich:
T1 rechts = [kr ; 100]IN
Also gilt für T Gewinne:
P(T ≥ kr) < 0,005
P(T ≤ kr–1) > 0,995
kr–1 ≥ 58 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
kr ≥ 59
 T1 rechts = [59 ; 100]IN
Also gilt für den gesamten Ablehnungsbereich:
T1 = [0 ; 31]IN
T1 rechts = [59 ; 100]IN
Also gilt für den gesamten Ablehnungsbereich:
T1 = [0 ; 31]IN 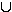 [59 ; 100]IN
Demnach kann bei 32 Gewinnspielen die Nullhypothese auf dem 1%-Niveau
nicht abgelehnt werden.
[59 ; 100]IN
Demnach kann bei 32 Gewinnspielen die Nullhypothese auf dem 1%-Niveau
nicht abgelehnt werden.
S II: Lösungen
1.1 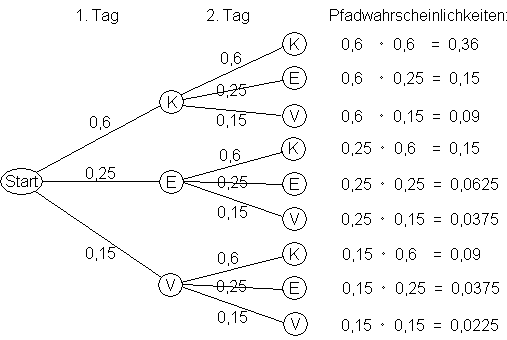 1.2 Bei den Teilaufgaben a) und c) liegt eine Bernoulli-Kette vor. Die WSK-Werte werden jeweils
dem Tafelwerk entnommen.
a) B(5; 0,6; 5) = 0,07776
c) B(5; 0,15; 0) = 0,44371
b)
1.2 Bei den Teilaufgaben a) und c) liegt eine Bernoulli-Kette vor. Die WSK-Werte werden jeweils
dem Tafelwerk entnommen.
a) B(5; 0,6; 5) = 0,07776
c) B(5; 0,15; 0) = 0,44371
b) 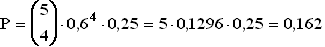 2.1 Einer Binomialverteilung liegt stets eine Bernoulli-Kette zugrunde.
Diese hat eine Länge (hier: n = 20), die Unterscheidung von „Treffer“ und „Niete“ (hier:
Vanillemilch bestellt: ja / nein) sowie eine konstante Trefferwahrscheinlichkeit (hier: p = 0,15).
Also ist die Zufallsgröße X binomial verteilt.
P(X ≤ 1) = F(1) = (Tafelwerk) 0,17556
2.2 P(X ≥ 2) = 1 – P(X ≤ 1) = 1 – F(1) = 1 – 0,17556 = 0,82444
3.1 Vierfeldertafel (gegebene Werte in Fettschrift):
2.1 Einer Binomialverteilung liegt stets eine Bernoulli-Kette zugrunde.
Diese hat eine Länge (hier: n = 20), die Unterscheidung von „Treffer“ und „Niete“ (hier:
Vanillemilch bestellt: ja / nein) sowie eine konstante Trefferwahrscheinlichkeit (hier: p = 0,15).
Also ist die Zufallsgröße X binomial verteilt.
P(X ≤ 1) = F(1) = (Tafelwerk) 0,17556
2.2 P(X ≥ 2) = 1 – P(X ≤ 1) = 1 – F(1) = 1 – 0,17556 = 0,82444
3.1 Vierfeldertafel (gegebene Werte in Fettschrift):
|
|
E1 (M)
|
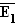
|
|
|
E2 (E)
|
0,15
|
0,10
|
0,25
|
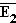
|
0,45
|
0,30
|
0,75
|
|
|
0,60
|
0,40
|
1
|
Aus der Vierfeldertafel folgt:
Die beiden Ereignisse sind vereinbar, weil P(E1  E2) = 0,15 > 0 .
Die beiden Ereignisse sind stochastisch unabhängig, wenn die „Erdbeermilch-Fraktion“
bei den Mädchen denselben Bruchteil ausmacht wie bei allen Kindern.
Das ist aber der Fall: 0,15 : 0,60 = 0,25 : 1 = 1 : 4 .
3.2 Wiederum gilt nach der Vierfeldertafel:
P(E1
E2) = 0,15 > 0 .
Die beiden Ereignisse sind stochastisch unabhängig, wenn die „Erdbeermilch-Fraktion“
bei den Mädchen denselben Bruchteil ausmacht wie bei allen Kindern.
Das ist aber der Fall: 0,15 : 0,60 = 0,25 : 1 = 1 : 4 .
3.2 Wiederum gilt nach der Vierfeldertafel:
P(E1 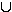 E2) = 0,60 + 0,25 – 0,15 = 0,70
P(
E2) = 0,60 + 0,25 – 0,15 = 0,70
P(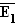

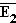 ) = 0,30
4.1 Wahrscheinlichkeitsverteilung von Y :
) = 0,30
4.1 Wahrscheinlichkeitsverteilung von Y :
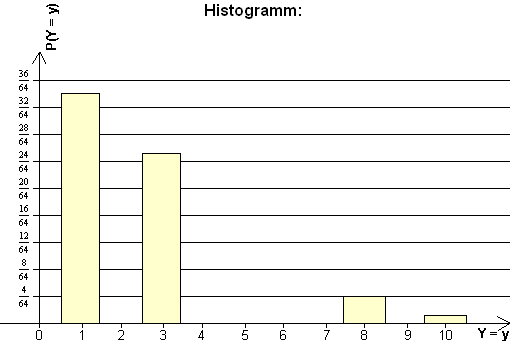 4.2 E(Y) = 1·
4.2 E(Y) = 1·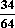 + 3·
+ 3·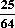 + 8·
+ 8·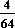 + 10·
+ 10·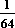 = 2,36
E(Y2) = 1·
= 2,36
E(Y2) = 1·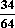 + 9·
+ 9·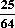 + 64·
+ 64·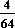 + 100·
+ 100·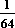 = 9,61
Var(Y) = E(Y2) – (E(Y))2 = 9,61 – 2,362 = 4,04
= 9,61
Var(Y) = E(Y2) – (E(Y))2 = 9,61 – 2,362 = 4,04  σ =
σ = 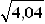 = 2,01
4.3 Testgröße T = Anzahl des erscheinenden blauen Sektors bei 50 Drehungen des Glücksrads
Nullhypothese: Der blaue Sektor erscheint unverändert mit der WSK p =
= 2,01
4.3 Testgröße T = Anzahl des erscheinenden blauen Sektors bei 50 Drehungen des Glücksrads
Nullhypothese: Der blaue Sektor erscheint unverändert mit der WSK p = 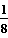 = 0,125.
Gegenhypothese: Der blaue Sektor erscheint mit einer WSK p >
= 0,125.
Gegenhypothese: Der blaue Sektor erscheint mit einer WSK p > 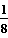 .
Art des Tests: einseitiger (rechtsseitiger) Hypothesentest
WSK, mit der T im Ablehnungsbereich liegt:
P(T > 10) = 1 – P(T ≤ 10) = 1 – F(10) = 1 – 0,95793 = 0,04207
.
Art des Tests: einseitiger (rechtsseitiger) Hypothesentest
WSK, mit der T im Ablehnungsbereich liegt:
P(T > 10) = 1 – P(T ≤ 10) = 1 – F(10) = 1 – 0,95793 = 0,04207
 2.1 P(A) = P({RRR, WWW}) = 0,12 + 0,024 = 0,144
P(B) = P({RRR, RRW, RWR, WRR}) = 0,12 + 0,18 + 0,18 + 0,168 = 0,648
Untersuchung von A und B auf stoch. Unabhängigkeit:
P(A
2.1 P(A) = P({RRR, WWW}) = 0,12 + 0,024 = 0,144
P(B) = P({RRR, RRW, RWR, WRR}) = 0,12 + 0,18 + 0,18 + 0,168 = 0,648
Untersuchung von A und B auf stoch. Unabhängigkeit:
P(A  B) = P({RRR}) = 0,12
P(A) · P(B) = 0,144 · 0,648 = 0,093312 ≠ 0,12 = P(A
B) = P({RRR}) = 0,12
P(A) · P(B) = 0,144 · 0,648 = 0,093312 ≠ 0,12 = P(A  B)
B)  A und B sind stochastisch abhängig.
2.2
A und B sind stochastisch abhängig.
2.2 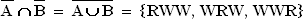 Es handelt sich um das Ereignis: „Es wird genau eine rote Kugel gezogen.“
P(
Es handelt sich um das Ereignis: „Es wird genau eine rote Kugel gezogen.“
P(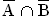 ) = 0,12 + 0,112 + 0,096 = 0,328
2.3
) = 0,12 + 0,112 + 0,096 = 0,328
2.3 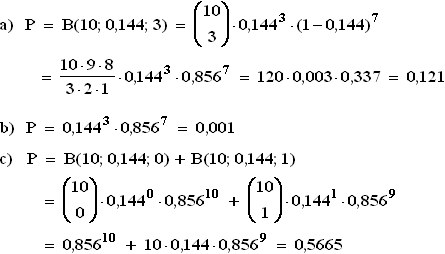 3.1
3.1 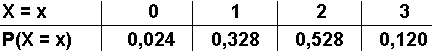 (Alle Werte sind dem Baumdiagramm von Aufgabe 1 entnommen.)
3.2
(Alle Werte sind dem Baumdiagramm von Aufgabe 1 entnommen.)
3.2 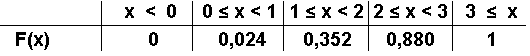 Graf der kumulativen Verteilungsfunktion F:
Graf der kumulativen Verteilungsfunktion F:
 4.1 Das Spiel ist fair, wenn E(X) = 0.
4.1 Das Spiel ist fair, wenn E(X) = 0.  a · 0,024 + 3 · 0,328 – 2 · 0,528 – 5 · 0,120 = 0
0,024 a = 0,672
a = 28
4.2
a · 0,024 + 3 · 0,328 – 2 · 0,528 – 5 · 0,120 = 0
0,024 a = 0,672
a = 28
4.2 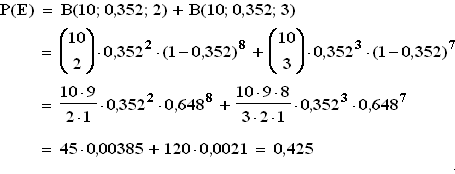
 P(
P(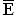 ) = 1 – 0,425 = 0,575 > P(E).
Also ist es günstiger, auf das Ereignis
) = 1 – 0,425 = 0,575 > P(E).
Also ist es günstiger, auf das Ereignis 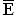 zu setzen.
5. Gegenhypothese: p ≠ 0,45
Linksseitiger Ablehnungsbereich:
T1 links = [0 ; kl]IN
Also gilt für T Gewinne:
P(T ≤ kl) < 0,005
kl ≤ 31 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
zu setzen.
5. Gegenhypothese: p ≠ 0,45
Linksseitiger Ablehnungsbereich:
T1 links = [0 ; kl]IN
Also gilt für T Gewinne:
P(T ≤ kl) < 0,005
kl ≤ 31 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
 T1 links = [0 ; 31]IN
Rechtsseitiger Ablehnungsbereich:
T1 rechts = [kr ; 100]IN
Also gilt für T Gewinne:
P(T ≥ kr) < 0,005
P(T ≤ kr–1) > 0,995
kr–1 ≥ 58 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
kr ≥ 59
T1 links = [0 ; 31]IN
Rechtsseitiger Ablehnungsbereich:
T1 rechts = [kr ; 100]IN
Also gilt für T Gewinne:
P(T ≥ kr) < 0,005
P(T ≤ kr–1) > 0,995
kr–1 ≥ 58 (laut Tafelwerk: p = 0,45; n = 100; rechte Spalte)
kr ≥ 59
 T1 rechts = [59 ; 100]IN
Also gilt für den gesamten Ablehnungsbereich:
T1 = [0 ; 31]IN
T1 rechts = [59 ; 100]IN
Also gilt für den gesamten Ablehnungsbereich:
T1 = [0 ; 31]IN 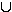 [59 ; 100]IN
Demnach kann bei 32 Gewinnspielen die Nullhypothese auf dem 1%-Niveau
nicht abgelehnt werden.
[59 ; 100]IN
Demnach kann bei 32 Gewinnspielen die Nullhypothese auf dem 1%-Niveau
nicht abgelehnt werden.
 1.2 Bei den Teilaufgaben a) und c) liegt eine Bernoulli-Kette vor. Die WSK-Werte werden jeweils
dem Tafelwerk entnommen.
a) B(5; 0,6; 5) = 0,07776
c) B(5; 0,15; 0) = 0,44371
1.2 Bei den Teilaufgaben a) und c) liegt eine Bernoulli-Kette vor. Die WSK-Werte werden jeweils
dem Tafelwerk entnommen.
a) B(5; 0,6; 5) = 0,07776
c) B(5; 0,15; 0) = 0,44371
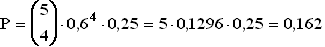 2.1 Einer Binomialverteilung liegt stets eine Bernoulli-Kette zugrunde.
Diese hat eine Länge (hier: n = 20), die Unterscheidung von „Treffer“ und „Niete“ (hier:
Vanillemilch bestellt: ja / nein) sowie eine konstante Trefferwahrscheinlichkeit (hier: p = 0,15).
Also ist die Zufallsgröße X binomial verteilt.
P(X ≤ 1) = F(1) = (Tafelwerk) 0,17556
2.2 P(X ≥ 2) = 1 – P(X ≤ 1) = 1 – F(1) = 1 – 0,17556 = 0,82444
3.1 Vierfeldertafel (gegebene Werte in Fettschrift):
2.1 Einer Binomialverteilung liegt stets eine Bernoulli-Kette zugrunde.
Diese hat eine Länge (hier: n = 20), die Unterscheidung von „Treffer“ und „Niete“ (hier:
Vanillemilch bestellt: ja / nein) sowie eine konstante Trefferwahrscheinlichkeit (hier: p = 0,15).
Also ist die Zufallsgröße X binomial verteilt.
P(X ≤ 1) = F(1) = (Tafelwerk) 0,17556
2.2 P(X ≥ 2) = 1 – P(X ≤ 1) = 1 – F(1) = 1 – 0,17556 = 0,82444
3.1 Vierfeldertafel (gegebene Werte in Fettschrift): 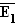
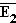
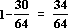
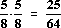
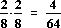
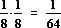
 4.2 E(Y) = 1·
4.2 E(Y) = 1·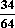 + 3·
+ 3·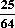 + 8·
+ 8·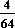 + 10·
+ 10·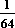 = 2,36
E(Y2) = 1·
= 2,36
E(Y2) = 1·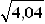 = 2,01
4.3 Testgröße T = Anzahl des erscheinenden blauen Sektors bei 50 Drehungen des Glücksrads
Nullhypothese: Der blaue Sektor erscheint unverändert mit der WSK p =
= 2,01
4.3 Testgröße T = Anzahl des erscheinenden blauen Sektors bei 50 Drehungen des Glücksrads
Nullhypothese: Der blaue Sektor erscheint unverändert mit der WSK p = 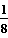 = 0,125.
Gegenhypothese: Der blaue Sektor erscheint mit einer WSK p >
= 0,125.
Gegenhypothese: Der blaue Sektor erscheint mit einer WSK p >