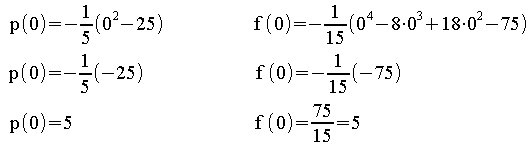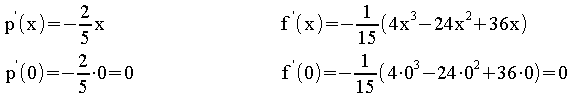Zu 2.:
Stetigkeit prüfen:
Es muss gelten: f (x ) = p (x
) = p (x )
)
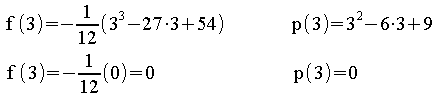
![]() f (x
f (x ) =
p (x
) =
p (x )
)
![]() Die Funktion g ist an
der Stelle x
Die Funktion g ist an
der Stelle x = 3 stetig.
= 3 stetig.
Differenzierbarkeit prüfen:
Es muss gelten:![]()
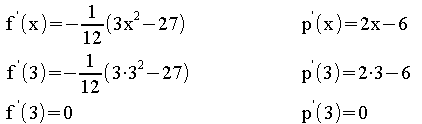
![]()
![]()
![]() Die Funktion g ist an
der Nahtstelle x
Die Funktion g ist an
der Nahtstelle x = 3 stetig und differenzierbar.
= 3 stetig und differenzierbar.
![]() Der Graph
G
Der Graph
G hat somit keinen „Sprung“ und keinen „Knick“.
hat somit keinen „Sprung“ und keinen „Knick“.
Zu 3.:
Stetigkeit ist gegeben
Differenzierbarkeit prüfen:
Es muss gelten:![]()

![]()
![]()
![]() Die Funktion f ist an
der Nahtstelle x
Die Funktion f ist an
der Nahtstelle x = 2 stetig, aber nicht differenzierbar.
= 2 stetig, aber nicht differenzierbar.
![]() Der Graph G
Der Graph G hat somit keinen „Sprung“, aber einen „Knick“.
hat somit keinen „Sprung“, aber einen „Knick“.
Zu 4.:
Differenzierbarkeit:
Es muss gelten:![]()

![]() Die Funktion k ist an
der Stelle x
Die Funktion k ist an
der Stelle x = 0 differenzierbar, wenn gilt: m = –1
= 0 differenzierbar, wenn gilt: m = –1
![]() Ergebnis:
Ergebnis:
![]()
Zu 5.:
Stetigkeit:
Es muss gelten: g1 (x ) = g2 (x
) = g2 (x )
)
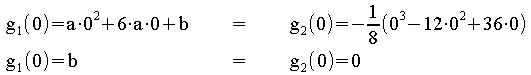
![]() Die Funktion g ist an
der Stelle x
Die Funktion g ist an
der Stelle x = 0 stetig, wenn gilt: b = 0
= 0 stetig, wenn gilt: b = 0
Differenzierbarkeit:
Es muss gelten:![]()
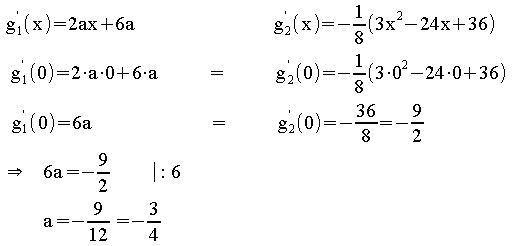
![]() Die Funktion g ist an
der Stelle x
Die Funktion g ist an
der Stelle x = 0 stetig und differenzierbar, wenn gilt:
= 0 stetig und differenzierbar, wenn gilt:
a =![]() und b = 0
und b = 0
![]() Ergebnis:
Ergebnis:![]()
Zu 6.:
Stetigkeit:
Es muss gelten: p (x ) = g (x
) = g (x )
)
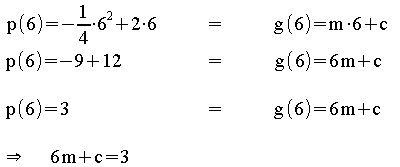
Differenzierbarkeit:
Es muss gelten:![]()
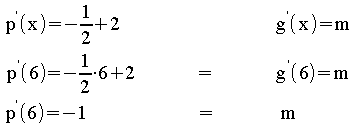
![]() Die Funktion k ist an
der Stelle x
Die Funktion k ist an
der Stelle x = 6 differenzierbar,wenn gilt: m = –1
= 6 differenzierbar,wenn gilt: m = –1
![]() m in die obere
Gleichung einsetzen und c ausrechnen:
m in die obere
Gleichung einsetzen und c ausrechnen:
![]() c = 9
c = 9
![]() Ergebnis: g(x) = – x + 9
Ergebnis: g(x) = – x + 9
Zu 7.:
Stetigkeit:
Es muss gelten: p (x ) = f (x
) = f (x )
)
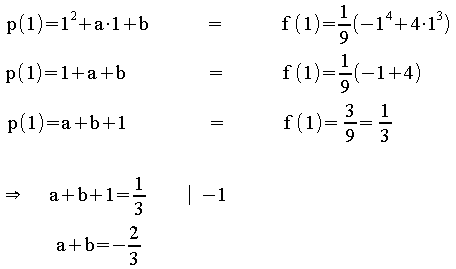
Differenzierbarkeit:
Es muss gelten:
![]()
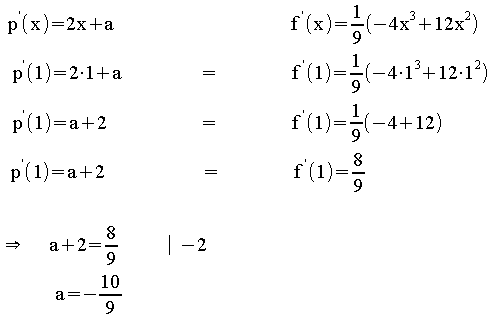
![]() Die Funktion g ist an
der Stelle x
Die Funktion g ist an
der Stelle x = 1 differenzierbar, wenn gilt:
= 1 differenzierbar, wenn gilt: 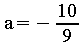
![]() a in die obere
Gleichung einsetzen und b ausrechnen
a in die obere
Gleichung einsetzen und b ausrechnen
![]()
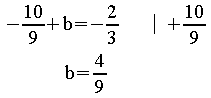
![]() Ergebnis:
Ergebnis:![]()
Zu 8.:
Stetigkeit:
Es muss gelten: f1 (x ) = f2 (x
) = f2 (x )
)
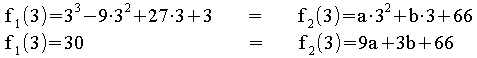
![]()
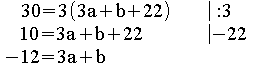
![]() Die Funktion f ist an
der Stelle x
Die Funktion f ist an
der Stelle x = 3 stetig, wenn gilt: I 3a + b = –12
= 3 stetig, wenn gilt: I 3a + b = –12
Differenzierbarkeit:
Es muss gelten:![]()
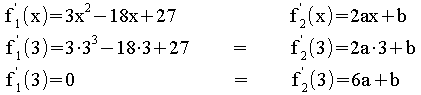
![]() Die Funktion f ist an
der Stelle x
Die Funktion f ist an
der Stelle x = 3 differenzierbar, wenn gilt:
= 3 differenzierbar, wenn gilt:
II 6a + b = 0
Gleichung I nach b auflösen und in II einsetzen:
![]() b = – 3a – 12
b = – 3a – 12
II '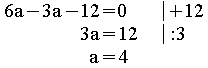
a = 4 in II einsetzen:
![]() 24 + b = 0
24 + b = 0 ![]() b = – 24
b = – 24
![]() Ergebnis:
Ergebnis:
- Für a = 4 und b = – 24 ist die Funktion f an der Stelle x
 = 3 stetig und differenzierbar.
= 3 stetig und differenzierbar.
- Die Stetigkeit bedeutet, dass eine kleine Änderung der Produktmenge in der
Umgebung von x
 = 3 nicht zu einer sprunghaften Änderung der Kosten führt.
= 3 nicht zu einer sprunghaften Änderung der Kosten führt.