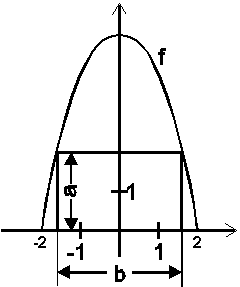
1. a)

Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: ![]() , also folgt:
, also folgt: ![]()
Zielfunktion: ![]()
Ableitungen: ![]()
![]()
Die Stelle -4![]() gehört nicht zum Definitionsbereich der Zielfunktion.
gehört nicht zum Definitionsbereich der Zielfunktion.
Da ![]() und
und ![]() hat die Zielfunktion an der Stelle
hat die Zielfunktion an der Stelle ![]() ein Maximum;
ein Maximum; 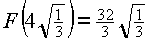 .
.
An den Randstellen gilt: 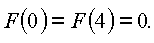
An den Randstellen wird ![]() nicht erreicht; an der Stelle
nicht erreicht; an der Stelle ![]() liegt also ein absolutes Maximum vor.
liegt also ein absolutes Maximum vor.
Das Rechteck hat genau dann maximalen Flächeninhalt, wenn gilt: ![]() .
.
b)
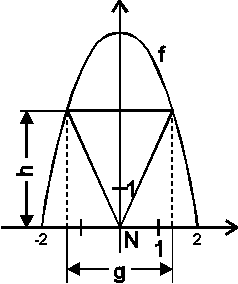
Extremalbedingung: 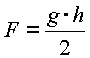 soll maximal werden.
soll maximal werden.
Nebenbedingung: 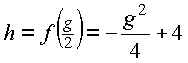
Also folgt: 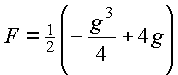
Zielfunktion: 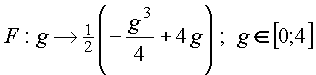
Ableitungen:
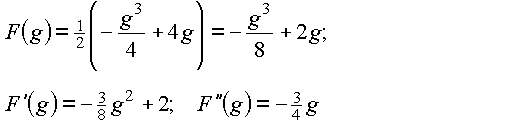
![]()
Die Stelle ![]() gehört nicht zum Definitionsbereich der Zielfunktion.
gehört nicht zum Definitionsbereich der Zielfunktion.
Da ![]() und
und ![]() , hat die Zielfunktion an der Stelle
, hat die Zielfunktion an der Stelle ![]() ein Maximum;
ein Maximum; 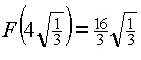 .
.
Für die Randstellen gilt: 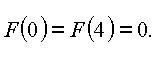
In den Randstellen wird ![]() nicht erreicht; an der Stelle
nicht erreicht; an der Stelle ![]() liegt also ein absolutes Maximum vor.
liegt also ein absolutes Maximum vor.
Das gleichschenklige Dreieck hat genau dann maximalen Flächeninhalt, wenn gilt: 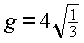 und
und 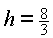 .
.
(Dieses Ergebnis war zu erwarten, denn anschaulich ist klar, dass das Dreieck genau dann maximalen Flächeninhalt hat, falls das "ergänzende" Rechteck größten Flächeninhalt hat. Aufgabenteil b) läßt sich also auf Aufgabenteil a) zurückführen.)
2.
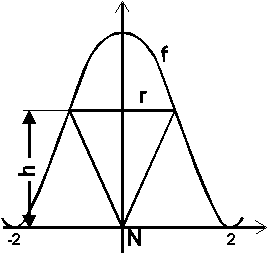
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung:
![]()
Also folgt:
![]()
Zielfunktion:
![]()
Ableitungen:
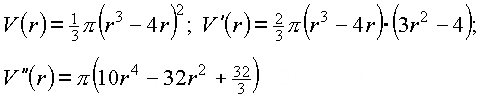
![]()
Die Stellen ![]() und
und ![]() gehören nicht zum Definitionsbereich der Zielfunktion.
gehören nicht zum Definitionsbereich der Zielfunktion.
Da ![]() und
und ![]() hat die Zielfunktion an der Stelle
hat die Zielfunktion an der Stelle ![]() ein Maximum.
ein Maximum.
Es gilt: ![]() und
und 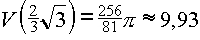
In den Randstellen wird ![]() nicht erreicht; an der Stelle
nicht erreicht; an der Stelle ![]() liegt also ein absolutes Maximum vor.
liegt also ein absolutes Maximum vor.
Der Kegel hat also genau dann ein maximales Volumen, falls ![]() und
und ![]() gilt.
gilt.
3.
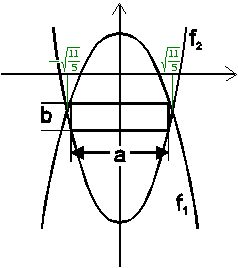
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung. ![]()
Also folgt: ![]()
Zielfunktion: ![]()
Ableitungen:
![]()
![]()
Die Stelle ![]() gehört nicht zum Definitionsbereich der Zielfunktion.
gehört nicht zum Definitionsbereich der Zielfunktion.
Da ![]() und
und ![]() hat die Zielfunktion an der Stelle
hat die Zielfunktion an der Stelle ![]() ein Maximum.
ein Maximum.
Es gilt: ![]()
In den Randstellen wird ![]() nicht erreicht; an der Stelle
nicht erreicht; an der Stelle ![]() liegt also ein absolutes Maximum vor.
liegt also ein absolutes Maximum vor.
Das Rechteck hat also genau dann maximalen Flächeninhalt, wenn ![]() und
und ![]() gilt.
gilt.
4. Seien die beiden gesuchten Summanden x und y.
a) Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: 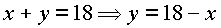
Zielfunktion:
![]()
Ableitungen:
![]()
![]()
Die Extremalstelle x=9 ist eine Maximalstelle, da ![]() ist.
ist.
Für x =9 und y= 9 wird das Produkt maximal.
b) Extremalbedingung: x2 + y2 soll minimal werden.
Nebenbedingung: 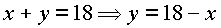
Zielfunktion: SQ(x) = x2 + (18 –x)2
![]()
Ableitungen: ![]()
![]()

Für x=9 und y=9 wird x2+y2 minimal.
5. Seien die beiden gesuchten Summanden x und y.
Extremalbedingung: x3.y2 soll maximal werden.
Nebenbedingung: ![]()
Zielfunktion:
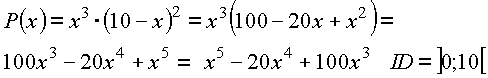
Ableitungen:
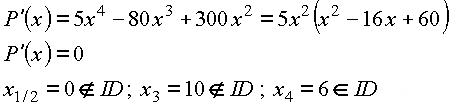
![]() für x=6
für x=6
Summanden sind x=6 und y=4.
![]()
6. Skizze:
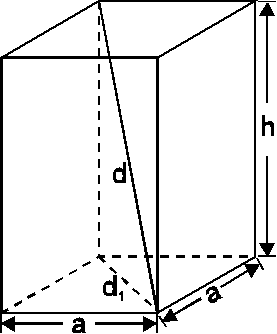
Extremalbedingung:
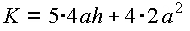 soll möglichst klein werden.
soll möglichst klein werden.
Nebenbedingung:
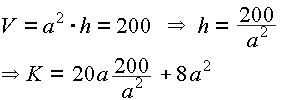
Zielfunktion:
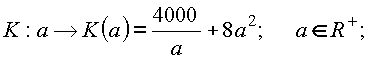
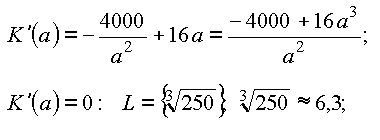
![]() hat an der Stelle
hat an der Stelle ![]() einen (–/+)- Vorzeichenwechsel, also liegt ein Minimum vor.
einen (–/+)- Vorzeichenwechsel, also liegt ein Minimum vor.
Es gilt:
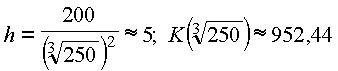
![]()
Randfälle: wenn ![]() , dann
, dann ![]() , wenn
, wenn ![]() , dann
, dann ![]()
Also sind die Kosten für 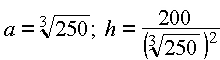 minimal.
minimal.
7. Gewinn: G
Preissenkung in Cents: x
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
(Erlös – Kosten in Cents)
![]()
![]()
![]() ,
, ![]()
Ableitungen: ![]()
![]()
![]()
Also ist x = 5 ein relatives Maximum und ![]()
Wegen ![]() und
und ![]() ist das relative Maximum auch das absolute Maximum.
ist das relative Maximum auch das absolute Maximum.
8. Skizze:
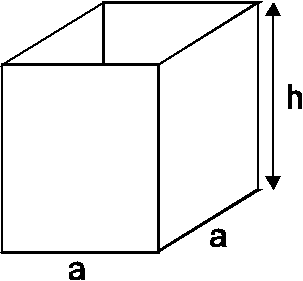
a) Extremalbedingung:
![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: 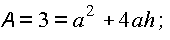 also
also 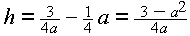
h ≥ 0  3 – a
3 – a ≥ 0
≥ 0  0 ≤ a ≤
0 ≤ a ≤ 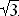
Also folgt: ![]()
Zielfunktion 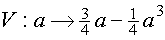 , 0 ≤ a ≤
, 0 ≤ a ≤ 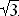
Ableitungen: ![]()
Bestimmen der relativen Extremstellen von ![]() :
:
![]()
![]()
Da ![]() und
und ![]() hat V an der Stelle 1 ein Maximum.
hat V an der Stelle 1 ein Maximum.
Randwerte: Es ist V(0) = 0 sowie V(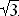 ) = 0. Es liegt daher an der Stelle 1 ein absolutes Maximum vor.
) = 0. Es liegt daher an der Stelle 1 ein absolutes Maximum vor.
Ein maximales Volumen liegt also für a = 1 dm und h = 0,5 dm vor.
Das Volumen beträgt dann ![]() .
.
b) Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: ![]() also
also 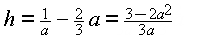
h ≥ 0  3 – 2a
3 – 2a ≥ 0
≥ 0  0 ≤ a ≤
0 ≤ a ≤ 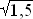
Also folgt: ![]()
Zielfunktion: 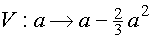 , 0 ≤ a ≤
, 0 ≤ a ≤ 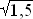
Ableitungen: ![]() ;
; 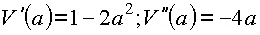
Bestimmen der relativen Extremstellen von 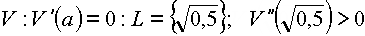
Also hat V an der Stelle 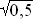 ein relatives Maximum.
ein relatives Maximum.
Ein maximales Volumen liegt bei ![]() vor. Es ist dann
vor. Es ist dann ![]()
Formulierung der Antwort analog zu a).
h : a = 4 : 3
Das Volumen der vorn geöffneten Schachtel ist etwas kleiner als das der oben geöffneten Schachtel.
9. Skizze:
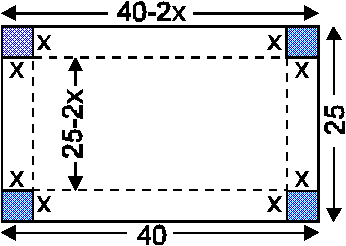
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Zielfunktion: ![]()
Ausmultiplizieren des Terms:
![]()
Ableitungen:
![]()
![]()
An der Stelle 5 hat die Zielfunktion ein Maximum (![]()
und V''(5) = –140 < 0).
Die Stelle ![]() gehört nicht zum Definitionsbereich der Zielfunktion.
gehört nicht zum Definitionsbereich der Zielfunktion.
Wegen ![]() liegt ein absolutes Maximum für x=5 vor.
liegt ein absolutes Maximum für x=5 vor.
Der Kasten mit den Maßen 30 cm, 15 cm und 5 cm hat maximales Volumen. Es beträgt 2250 cm![]() .
.
10. Skizze:
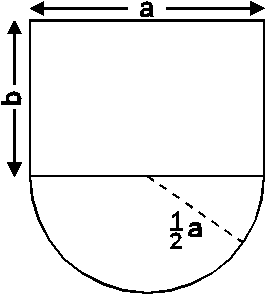
Extremalbedingung: 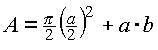 soll maximal werden.
soll maximal werden.
Nebenbedingung: ![]()
b ≥ 0 
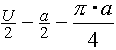 ≥ 0
≥ 0  a ≤
a ≤ 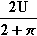
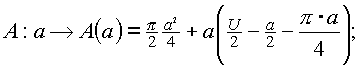 , 0 ≤ a ≤
, 0 ≤ a ≤ 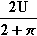
![]()
![]()
![]()
 Bei a =
Bei a = 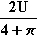 ist ein relatives Maximum.
ist ein relatives Maximum.
Randfälle: A(0) = 0; A(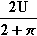 ) ≈ 0,06U
) ≈ 0,06U < A(
< A(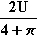 ) ≈ 0,1U
) ≈ 0,1U

Für a = 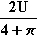 ist der Funktionswert maximal. Es folgt: b =
ist der Funktionswert maximal. Es folgt: b = 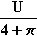 , d. h.
, d. h.
11. Skizze:
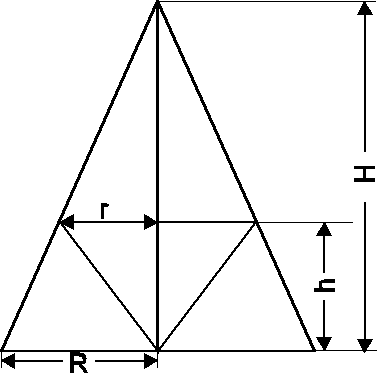
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: ( mit Hife des Strahlensatzes zu berechnen): ![]()

![]()
![]()
![]()
Zielfunktion: ![]()
Ableitungen: ![]()
![]()
Bestimmung der Maximalstelle:
![]()
Die Stelle 0 ist eine Randstelle.
Da ![]() und
und ![]() hat die Zielfunktion an der Stelle
hat die Zielfunktion an der Stelle ![]() ein Maximum;
ein Maximum; 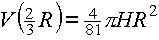 .
.
An den Randstellen gilt: 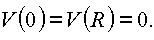 .
.
In den Randstellen wird ![]() nicht erreicht; an der Stelle
nicht erreicht; an der Stelle ![]() liegt also ein absolutes Maximum vor.
liegt also ein absolutes Maximum vor.
Ein maximales Volumen liegt also genau dann vor, wenn ![]() und
und ![]() gilt.
gilt.
Das Volumen ist dann ![]() .
.
12. Skizze:
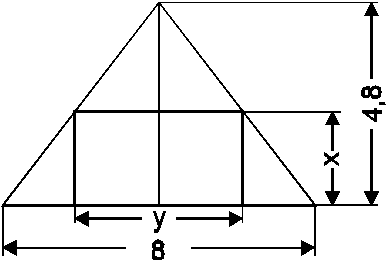
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: 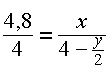
Es gilt:
![]()
Zielfunktion: ![]()
Ableitungen: ![]()
Bestimmung der Maximalstelle:
![]()
Da ![]() und
und ![]() hat die Zielfunktion an der Stelle 4 ein Maximum;
hat die Zielfunktion an der Stelle 4 ein Maximum; 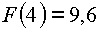 .
.
An den Randstellen gilt: 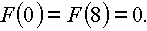
In den Randstellen wird ![]() nicht erreicht; an der Stelle 4 liegt also ein absolutes Maximum vor.
nicht erreicht; an der Stelle 4 liegt also ein absolutes Maximum vor.
Das quaderförmige Zimmer ist genau dann möglichst groß, wenn y=4 und x=2,4 gilt.
Es muss also eine Höhe von 2,4 m und eine Breite von 4 m gewählt werden.
13. Skizze:

Extremalbedingung: ![]() soll minimal werden.
soll minimal werden.
Nebenbedingung: ![]() d.h.
d.h. ![]()
Also folgt mit ![]()
Zielfunktion: ![]()
Ableitung: 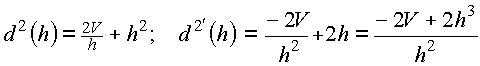
Bestimmung der Minimalstelle:
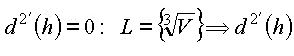 hat an der Stelle h =
hat an der Stelle h = ![]() einen
einen
![]() - Vorzeichenwechsel, es liegt ein relatives Minimum vor.
- Vorzeichenwechsel, es liegt ein relatives Minimum vor.
Das Minimum ist für ![]() gegeben.
gegeben.
Randstellen: Wenn ![]() , dann
, dann ![]() ; wenn
; wenn ![]() , dann
, dann ![]()
Es liegt ein absolutes Minimum vor.
Begründung: Wegen der Monotonie der Quadratfunktion hat mit einer Funktion f auch die Funktion ![]() an einer Stelle ein Extremum.
an einer Stelle ein Extremum.
Maße der gesuchten quadratischen Säule:
a = ![]() ; h =
; h = ![]() ,
,
d. h.: die gesuchte quadratische Säule ist ein Würfel.
14. Skizze:
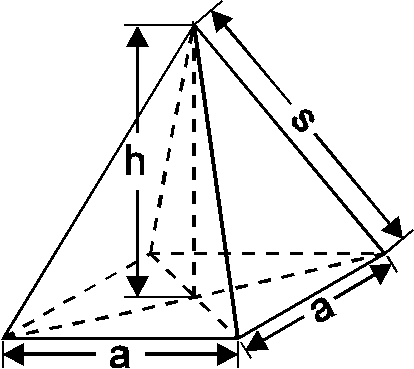
Extremalbedingung: s möglichst klein
Nebenbedingung: 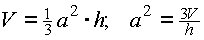
![]()
![]()
Zielfunktion: ![]()
Ableitung: 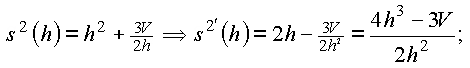
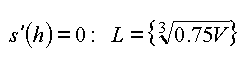
![]() hat an der Stelle
hat an der Stelle ![]() einen (–/+)-Vorzeichenwechsel: Es liegt ein Minimum vor.
einen (–/+)-Vorzeichenwechsel: Es liegt ein Minimum vor.
Es ergibt sich
![]()
d.h.
![]()
Wenn ![]() , dann
, dann ![]() ; wenn
; wenn ![]() , dann
, dann ![]() . Es liegt also ein absolutes Minimum vor.
. Es liegt also ein absolutes Minimum vor.
Maße der gesuchten geraden quadratischen Pyramide:
a =  ; h =
; h = 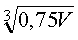 = 0,5 ·
= 0,5 ·  ,
,
d. h. a : h = 2 : 1.
15. Skizze:
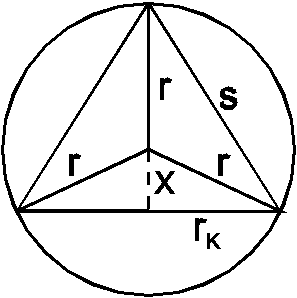
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: es muss gelten: I. ![]()
II. x2 + rk2 = r2  x =
x = 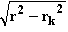
Setzt man x in die erste Gleichung ein, so erhält man:
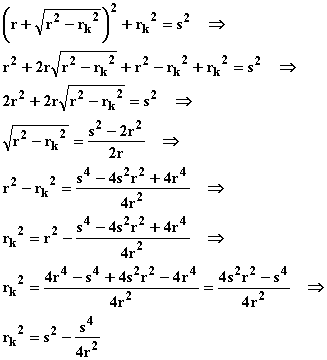
Damit ergibt sich: ![]()
bzw. ![]()
Zielfunktion: ![]()

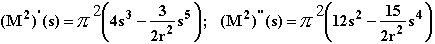
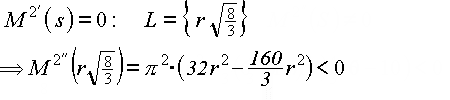
Also liegt ein relatives Maximum vor.
Aus ![]() ergibt sich
ergibt sich ![]()
Da gilt ![]() , liegt ein absolutes Maximum vor.
, liegt ein absolutes Maximum vor.
Maße des gesuchten geraden Kreiskegels:
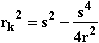 ergibt mit
ergibt mit 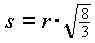 den Grundflächenradius r
den Grundflächenradius r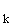 =
= 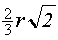 ;
;
Kegelhöhe: h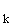 =
= 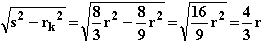 ,
,
d. h. r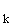 : h
: h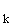 = 1 :
= 1 : 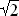 .
.
16. a)
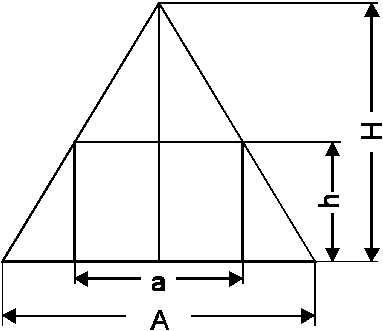
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung (Strahlensatz): ![]() hieraus folgt
hieraus folgt ![]()
![]()
Ziefunktion: ![]()
Ableitungen: ![]()
![]()
An der Stelle a = ![]() liegt also ein Maximum vor.
liegt also ein Maximum vor.
Wegen ![]() liegt ein absolutes Maximum vor.
liegt ein absolutes Maximum vor.
Das größte Volumen ist für ![]() gegeben. Es beträgt:
gegeben. Es beträgt: ![]()
b)
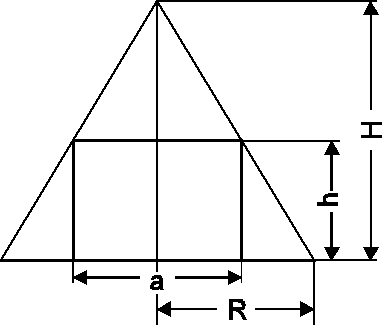
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: 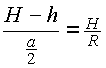 ; hieraus folgt
; hieraus folgt ![]() , also
, also ![]()
Zielfunktion: ![]()
Ableitungen: ![]()
![]()
An der Stelle a = ![]() liegt also ein Maximum vor.
liegt also ein Maximum vor.
Wegen ![]() liegt ein absolutes Maximum vor.
liegt ein absolutes Maximum vor.
Für ![]() liegt der größte Wert des Volumens vor. Er beträgt
liegt der größte Wert des Volumens vor. Er beträgt ![]() .
.
17.
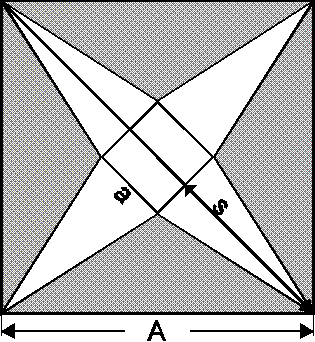
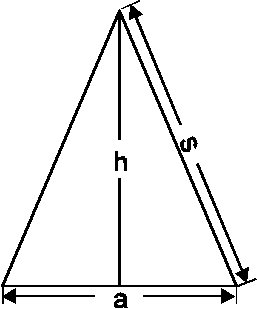
Extremalbedingung: ![]() soll maximal werden.
soll maximal werden.
Nebenbedingung: ![]() d.h.
d.h.
![]()
Durch das Einsetzen von s ergibt sich:
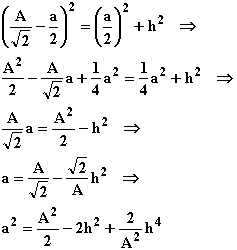
a2 einsetzen in V ergibt:
![]()
Zielfunktion: 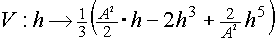
Definitionsmenge von V: h < halbe Diagonale des großen Quadrats
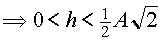
Ableitungen:
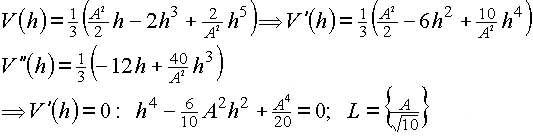
( Die 2. Lösung h = 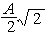 entfällt, da sie nicht im Definitionsbereich liegt.)
entfällt, da sie nicht im Definitionsbereich liegt.)
![]()
Es liegt also ein Maximum vor.
Wegen ![]() liegt ein absolutes Maximum vor.
liegt ein absolutes Maximum vor.
Ein Maximum liegt für 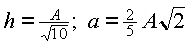 vor.
vor.
Das Volumen beträgt dann 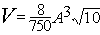 .
.
18. a)
Skizze:
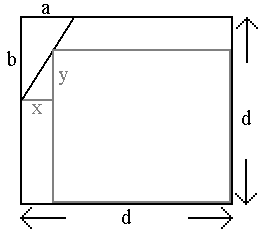
Extremalbedingung: F = (d – x)(d – (b – y)) soll maximal werden.
Nebenbedingung: 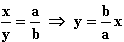
y, a = 0,4, b = 0,5, d = 1 in F eingesetzt 
Zielfunktion: F: x 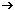 F(x) = (1 – x)
F(x) = (1 – x)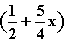 =
= 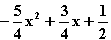 , 0 ≤ x ≤ 0,4
, 0 ≤ x ≤ 0,4
Ableitungen: 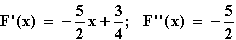
F '(x) = 0  x = 0,3
x = 0,3 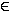 IDF
IDF
F ''(x) < 0  Bei x = 0,3 hat F das relative Maximum
Bei x = 0,3 hat F das relative Maximum
Randwerte: F(0) = 0,5 < F(0,3); F(0,4) = 0,6 < F(0,3) 
Das relative Maximum bei x = 0,3 ist das absolute Maximum von F.
Maße der Scheibe mit maximaler Fläche:
Breite: 1 – 0,3 = 0,7 m; Höhe: 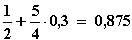 m.
m.
b)
Skizze:

Extremalbedingung: F = (d – x)(d – (b – y)) soll maximal werden.
Nebenbedingung: 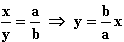
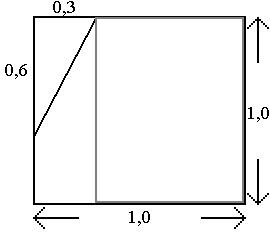
y, a = 0,3, b = 0,6, d = 1 in F eingesetzt 
Zielfunktion: F: x 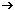 F(x) = (1 – x)(0,4 + 2x) = –2x2 + 1,6x + 0,4; 0 ≤ x ≤ 0,3
F(x) = (1 – x)(0,4 + 2x) = –2x2 + 1,6x + 0,4; 0 ≤ x ≤ 0,3
Ableitungen: F '(x) = –4x + 1,6; F ''(x) = –4
F '(x) = 0  x = 0,4
x = 0,4 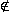 IDF
IDF 
Das Maximum von F muss ein Randwertmaximum sein.
F(0) = 0,4; F(0,3) = 0,7 > F(0) 
An der Randstelle x = 0,3 liegt das absolute Maximum von F vor.
Maße der Scheibe mit maximaler Fläche:
Breite: 1 – 0,3 = 0,7 m; Höhe: 1 m.
Skizze: