Gemischte Aufgaben
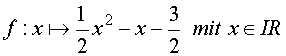1.	Gegeben ist die Funktion . Ihr Graph heißt  Gf.
	a)	Bestimmen Sie die Koordinaten der Schnittpunkte von  Gf  mit den Koordinatenachsen sowie die des Scheitels! Zeichnen Sie  Gf  im Intervall  [-3 ; 5] !
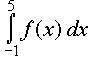	b)	Berechnen Sie !   Wie lässt sich das Ergebnis geometrisch deuten?
2.	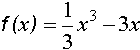Es ist die Gesamtfläche zwischen dem Graphen der Funktion  f  mit     und der x-Achse zu berechnen.
3.	Der Graph der Funktion  f  mit der Gleichung  f(x) = –2x3 – 3x2  begrenzt mit den Koordinatenachsen eine Fläche. Berechnen Sie ihren Inhalt!
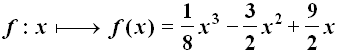4.	Der Graph der Funktion    begrenzt mit der x-Achse eine Fläche. In welchem Verhältnis teilt die durch den Ursprung und den Hochpunkt von  Gf  gelegte Gerade diese Fläche?
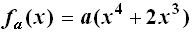5.	Gegeben sind die Funktion und die Grenzen 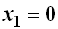und 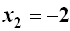. Berechnen Sie  a, wenn die Fläche 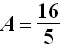  betragen soll.
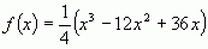6.	Die Gerade mit der Gleichung  x = u,  0 < u < 4,  schneidet den Graphen der Funktion im Punkt  U  und den Graphen der Funktion 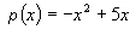im Punkt  V.   W ist der Berührpunkt der beiden Graphen. Zeigen Sie, dass für die von  u  abhängige Flächenmaßzahl  A(u)  des Dreiecks UVW gilt: 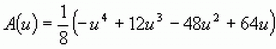. Untersuchen Sie außerdem, für welchen Wert von  u  das zugehörige Dreieck UVW den absolut größten Flächeninhalt besitzt.
Lösungen                     zu den Übungsblättern