Also gilt
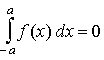 .
.
Also gilt
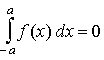 .
.
Also gilt
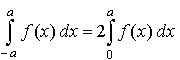 .
.
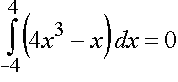
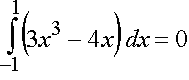
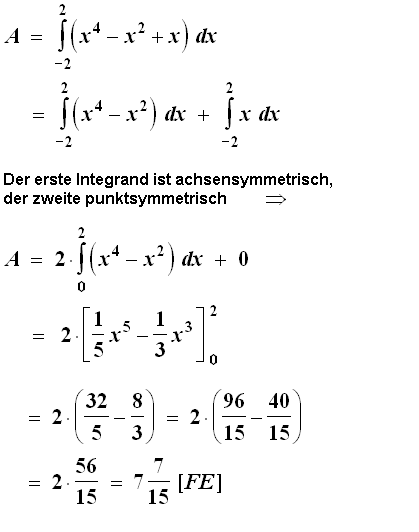
| Lösung zu den Aufgaben zur Symmetrie | |
| 1. |
a) Der Graph von f ist punktsymmetrisch zum Koordinatenursprung. Also gilt 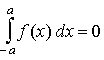 . .
|
| b) Der Graph von f zeigt keine Symmetrie. Folglich gilt keine der beiden Formeln. | |
|
c) Der Graph von f ist punktsymmetrisch zum Koordinatenursprung. Also gilt 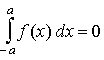 . .
|
|
|
d) Der Graph von f ist achsensymmetrisch zur y-Achse. Also gilt 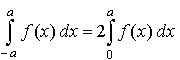 . .
|
|
| 2. Wir untersuchen, ob sich die Integrandenfunktion f durch eine besondere Symmetrie auszeichnet. | |
a) Der Graph von f ist punktsymmetrisch bzgl. O. Also gilt: 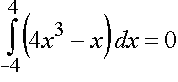
|
|
b) Der Graph von f ist punktsymmetrisch bzgl. O. Also gilt: 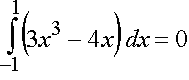
|
|
c) f zeigt keine Symmetrie. Aber man kann f in zwei symmetrische Funktionen zerlegen: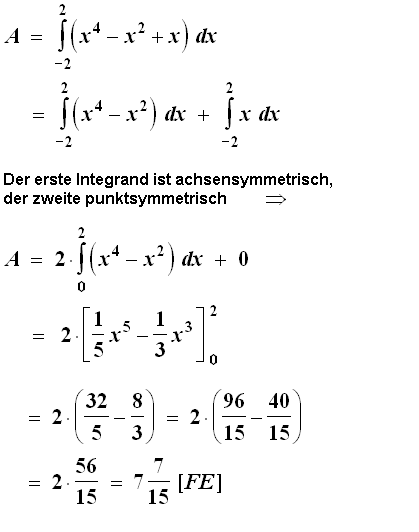
|
|