
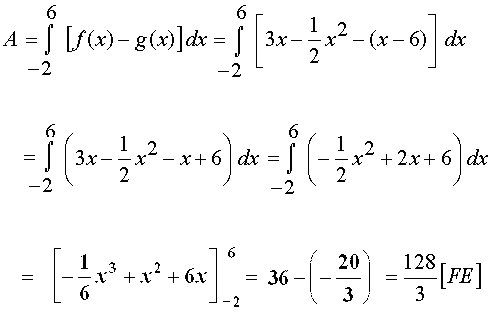
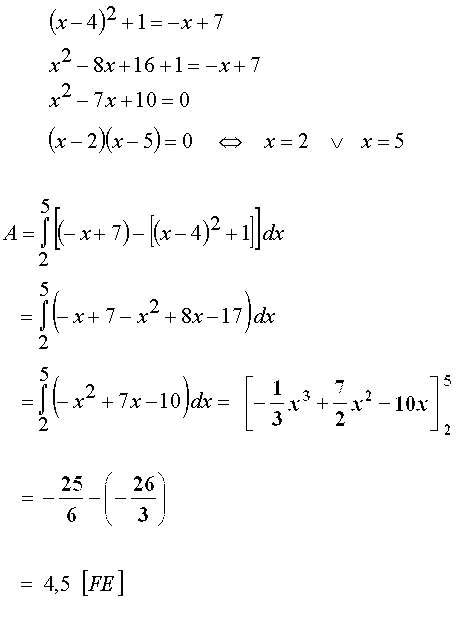
in ihrem Scheitel und schneidet die Gerade g(x) = –x + 7 bei x = 6.
Nach a) schneiden sich die Graphen von f und g bei x = 5.
Folglich muss im Intervall [4; 5] über f(x) – 1 und im Intervall [5; 6] über
g(x) – 1 integriert werden:
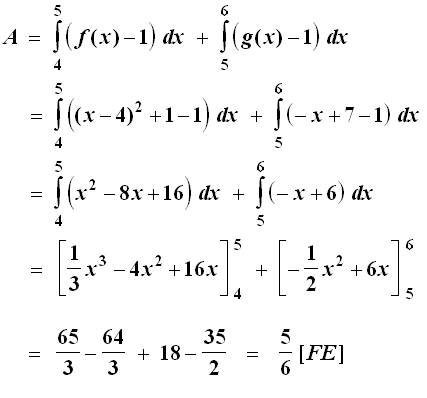
| Lösungen zu den Aufgaben zu Flächen zwischen zwei Funktionsgraphen | |
| 1. | Wir bestimmen die x-Koordinaten der Schnittpunkte beider Graphen. Wir setzen dazu die Funktionsterme einander gleich: |

|
|
| Da z. B. f(0) = 0 > g(0) = – 6, gilt im schnittstellenfreien Intervall ]–2; 6[: f(x) > g(x). Also ergibt sich der Integralansatz: | |
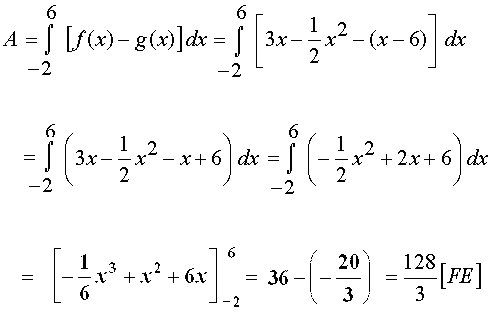
|
|
| 2. |
a) Zunächst werden die Schnittstellen bestimmt: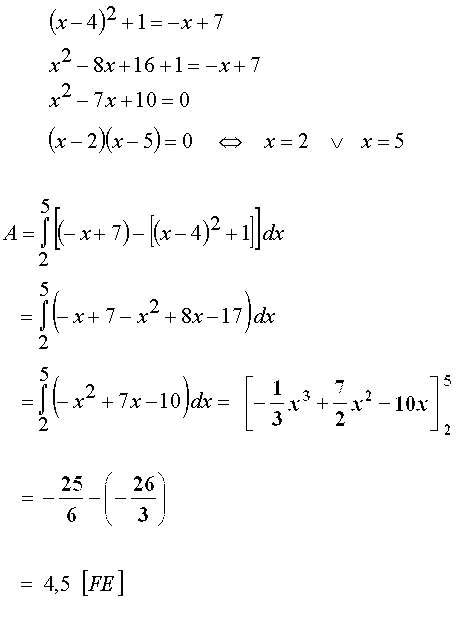
|
|
b) Da die Parabel Gf den Scheitel S(4 | 1) besitzt, berührt die Gerade y = 1 sie in ihrem Scheitel und schneidet die Gerade g(x) = –x + 7 bei x = 6. Nach a) schneiden sich die Graphen von f und g bei x = 5. Folglich muss im Intervall [4; 5] über f(x) – 1 und im Intervall [5; 6] über g(x) – 1 integriert werden: 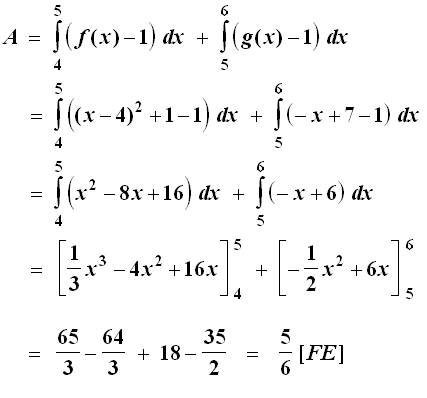
|
|