1.

a)

f(3) = –9 < 0 und  f(4) = 9 > 0  

Im Intervall  I = [3;4] existiert mindestens eine Nullstelle.

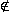f '(x) = 3x² – 4x – 5 = 0     x₁ ≈ 2,1 I  und  x₂ ≈ –0,8 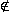I  

Im Intervall  I = [3;4] ist f streng monoton, besitzt also nur eine Nullstelle x₀.

Bestimmung des günstigeren Startwertes:

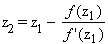|f '(3)| = 10 und |f '(4)| = 27 > |f '(3)| Startwert z₁ = 4.

  =  4 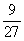– = 3,67

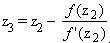  =  3,67 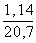– = 3,615

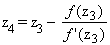  =  3,615 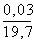– = 3,613

Die gesuchte Nullstelle lautet: x₀ = 3,61.

b)

f(3) = –13 < 0 und  f(4) = 9 > 0  

Im Intervall  I = [3;4] existiert mindestens eine Nullstelle.

f '(x) = 3x² – 2x – 8 = 0     x₁ = 2 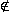I  und  x₂ =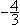 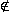I  

Im Intervall  I = [3;4] ist f streng monoton, besitzt also nur eine Nullstelle x₀.

Bestimmung des günstigeren Startwertes:

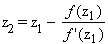|f '(3)| = 13 und |f '(4)| = 32 > |f '(3)| Startwert z₁ = 4.

  =  4 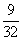– = 3,72

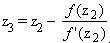  =  3,72 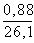– = 3,686

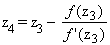  =  3,686 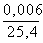– = 3,686

Die gesuchte Nullstelle lautet: x₀ = 3,69.

c)

f(–2) = –3 < 0 und  f(–1,5) = 7,5 > 0  

Im Intervall  I = [–2;–1,5]  existiert mindestens eine Nullstelle.

f '(x) = 5x⁴ – 9x² = 0     x_1/2 = 0 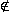I,   x_3/4 ≈ ±1,34 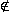I    

Im Intervall  I = [–2;–1,5] ist f streng monoton, besitzt also nur eine Nullstelle x₀.

Bestimmung des günstigeren Startwertes:

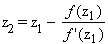|f '(–2)| = 44 und |f '(–1,5)| = 5,1 < |f '(–2)| Startwert z₁ = –2.

  =  –2 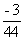– = –1,93

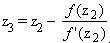  =  –1,93 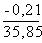– = –1,924

Die gesuchte Nullstelle lautet: x₀ = –1,92.

d)

f(1) = –2 < 0 und  f(2) = 36 > 0  

Im Intervall  I = [1;2] existiert mindestens eine Nullstelle.

f '(x) = 5x⁴ + 3x² = 0     x_1/2 = 0 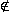I  

Im Intervall  I = [1;2] ist f streng monoton, besitzt also nur eine Nullstelle x₀.

Bestimmung des günstigeren Startwertes:

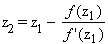|f '(1)| = 8 und |f '(2)| = 92 > |f '(1)| Startwert z₁ = 2.

  =  2 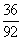– = 1,61

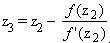  =  1,61 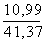– = 1,344

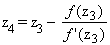  =  1,344 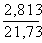– = 1,215

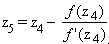  =  1,215 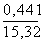– = 1,186

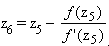  =  1,186 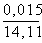– = 1,185

Die gesuchte Nullstelle lautet: x₀ = 1,18.