Übungsblatt
zur stochastischen (Un-)abhängigkeit
Seminararbeit von Katharina Hoffmann 2003
Nachbearbeitung: OStR Starfinger
1.
Eine Laplace-Münze wird dreimal geworfen. Dabei sind folgende Ereignisse definiert:
A:"beim ersten Wurf Zahl"; B:"beim zweiten Wurf Zahl"; C:"genau zweimal hintereinander Zahl".
Zeigen Sie, dass a) A und C unabhängig sind; b) B und C abhängig sind. Art der Abhängigkeit?
2.
Beim mehrfachen Werfen einer Laplace-Münze sind die beiden Ereignisse A und B definiert durch A:"beide Seiten der Münze werden sichtbar" und B:"es tritt höchstens einmal Zahl auf".
Zeigen Sie, dass
a.) A und B abhängig sind, wenn die Münze zweimal geworfen wird.
b.) A und B unabhängig sind, wenn die Münze dreimal geworfen wird.
3.
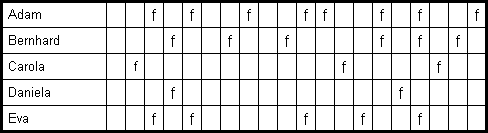
In der Absenzenliste eines Kurses sind Fehlstunden durch ein „f “ gekennzeichnet. Zeige, dass das Fehlen von Adam und Eva stochastisch abhängig ist, und interpretiere das Ergebnis!
4.
Tankstellenbesitzer T weiß aus Erfahrung, dass 30% seiner Kunden Superbenzin tanken, wobei 40% von diesen die Automarke M fahren. Außerdem weiß er, dass 42% aller seiner Kunden weder Fahrer der Marke M sind noch Superbenzin tanken.
Geben Sie eine vollständige Vierfeldertafel an und überprüfen Sie die Ereignisse S:"Tanken von Superbenzin" und M:"Fahrer der Automarke M" auf Unabhängigkeit.
zurück zur Startseite
