0 = a0³
+ b0² + c0 + d 
d
= 0 f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
WP:
(1) f (0) = 0 0 = a0³
+ b0² + c0 + d d
= 0
(2) f ''(0) = 0
0 = 6a0 + 2b b
= 0
EP:
(3) f (-1) = 4
4 = -a + b - c + d
(4) f ' (-1) = 0
0 = 3a - 2b + c
(3) 4 = -a - c (b,d eliminiert)
a = 2
0 = 6 + c
c = -6
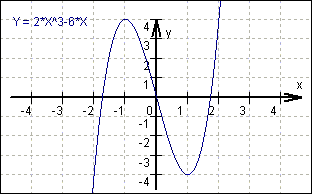
Ergebnis: f (x) = 2x³ - 6x
f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
0(0/0):
f (0) = 0 0 = a0³ + b0²
+ c0 + d d = 0
f '(0) = 0 0 = 3a0² + 2b0
+c c = 0
P(-6/0):
(1) f (-6) = 0 0 = -216a +
36b - 6c + d
(2) f '(-6) = 
= 108a - 12b + c
(1) 0 = -216a + 36b
(2)
= 108a - 12b
[(1) + 2(2)] 9 = 12b
b = 0,75
a = (36 * 0,75) / 216 a
= 0,125
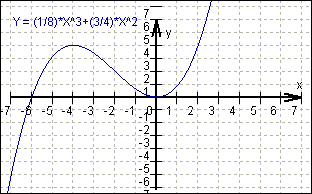
Ergebnis: f (x) = 0,125x³ + 0,75x²
f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
g(x) = 
x³
- 2x
gleiche Nullstellen:
g(x) = 0
0 =
x³ - 2x
0 = x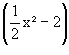 
x1
= 0; x2 = -2; x3 = 2
(-2/0); (0/0); (2/0) sind auch Punkte des Graphen Gf
(1) f (-2) = 0 0 = -8a + 4b
- 2c + d
(2) f (0) = 0 0 = a0³
+ b0² + c0 + d
d = 0
(3) f(2) = 0 0 = 8a + 4b +
2c + d
In (0/0) schneiden sich die Tangenten senkrecht:
f '(0)
= 
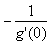
g '(x) = 1
x² - 2
g '(0)
= -2
f '(0) =
= 3a0² + 2b0 + c
c =
b = 0
In (3): 0 = 8a + 1 a
= - 
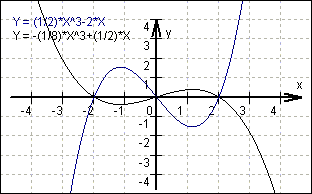
Ergebnis: f (x) = - x³
+ x
f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
0(0/0):
(1) f (0) = 0 0 = a0³
+ b0² + c0 + d d
= 0
W(2/1):
(2) f (2) = 1 1 = 8a + 4b +
2c
(3) f ''(2) = 0 0 = 12a + 2b
Steigung in W ist -1,5:
(4) f '(2) = -1,5 -1,5 = 12a
+ 4b +c
(4)-(2) = (5):
-2 = 8a + 2b
(3)-(5):
2 = 4a a =
in (5) b = -3
in (2) c = 4,5
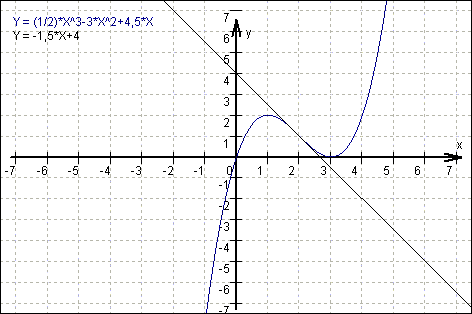
Ergebnis: f(x) = x³
- 3x² + 4,5x
f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
WP(0/0):
(1) f (0) = 0 a0³ + b0²
+ c0 + d d = 0
(2) f ''(0) = 0 0 = 6a0 + 2b
b = 0
P(-2/2):
(3) f (-2) = 2 2 = -8a - 2c
(4) f '(-2) = 0 0 = 12a + c
(4) * 2 + (3):
2 = 16a a =
a in (4):
0 = 12 *
+ c c = -1
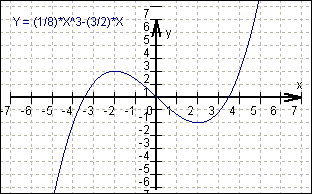
Ergebnis: f (x) = x³
- 1x
f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
A(2/3):
(1) f (2) = 3 3 = 8a + 4b +
2c + d
(2) f '(2) = -9 -9 = 12a +
4b + c
EP:
(3) f '(-1) = 0 0 = 3a - 2b
+ c
WP(0/y0):
(4) f ''(0) = 0 0 = 6a0 + 2b
b = 0
a = -1
a in (3):
0 = 3 * (-1) + c c
= 3
c in (1):
3 = -8 + 6 + d d
= 5
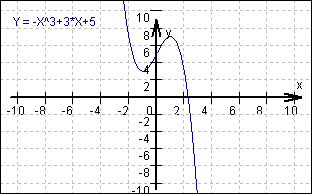
Ergebnis: f (x) = -x³ + 3x + 5
f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
(1) f (0) = 0 a0³ + b0²
+ c0 + d d = 0
(2) f (2) = 1 1 = 8a + 4b +
2c
(3) f ''(2) = 0 0 = 12a + 2b
(4) f '(2) = 0 0 = 12a + 4b
+ c
(2) - (4)*2 = (5) :
(5) 1 = -16a - 4b a=
a in (3):
0 = 
+ 2b
b = -
a und b in (4):
0 = - 3 +
c c =
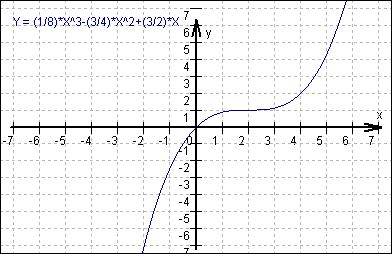
Ergebnis: f (x) = x³
- x²
+ x
f (x) = ax³ + bx² + cx + d
f ' (x) = 3ax² + 2bx + c
f '' (x) = 6ax + 2b
Tangente: t (x) = -3x + 6
t (2) = 0 P1(2/0) mit der
Steigung m = -3
(1) f (0) = -2 -2 = a0³
+ b0² + c0 + d d
= -2
(2) f (2) = 0 0 = 8a + 4b + 2c - 2
(3) f '(2) = -3 -3 = 12a +
4b + c
(4) f ''(2) = 0 0 = 12a + 2b
(1) - (3)*2 = (5) : 6 = -16a - 4b -2
(5) 6 = -16a - 4b -2
(4) 0 = 12a + 2b
(5) + (4)*2:
6 = 8a -2 a
= 1
a in (4):
0 = 12 + 2b b
= -6
a und b in (3):
-3 = 12 + 4*(-6) + c c
= 9
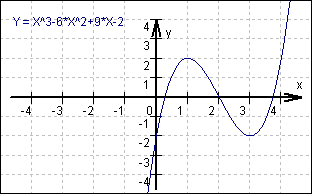
Ergebnis: x³ - 6x² + 9x - 2
Symmetrie zur y-Achse
f (x) = ax4 + bx2 + c
f ' (x) = 4ax³ + 2bx
f '' (x) = 12ax² + 2b
P(2/0):
(1) f (2) = 0 0 = 16a + 4b
+ c
m = 2 :
(2) f '(2) = 2 2 = 32a + 4b
WP:
(3) f ''(-1) = 0 0 = 12a +
2b
(2) 2 = 32a + 4b
(3) 0 = 12a + 2b
(2) - (3)*2:
2 = 8a a = 
a in (3):
0 = 3 + 2b b
= -
a und b in (1):
0 = 4 - 6 + c c = 2
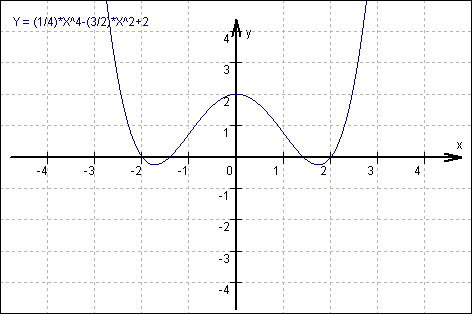
Ergebnis: f (x) = x4
- x2 + 2
Da die Grafen der Schar achsensymmetrisch sein sollen, fallen alle Glieder des Funktionsterms mit ungeraden Exponenten weg.
fa (x) = ax4 + cx2 + e
fa' (x) = 4ax3 + 2cx
P(0/2):
fa (0) = 2 a04
+ c02 + e e
= 2
fa' (1) = 12 12 = 4a +
2c c = 6 - 2a
fa (x) = ax4 + (6 - 2a)x2 + 2
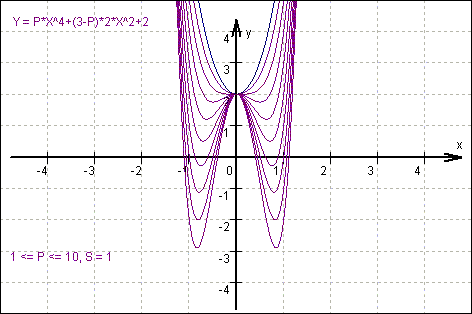
Ergebnis: fa (x) = ax4 + (3 - a)2x + 2
