Lösungen

1. Regeln

1.1. Die Verzweigungsregel:
Die Summe der Wahrscheinlichkeiten, die von einem Verzweigungspunkt ausgehen, ist eins.

1.2. Die erste Pfadregel:
Die Wahrscheinlichkeit, dass ein bestimmtes Elementarereignis eintritt, wird dadurch errechnet, dass die Einzellwahrscheinlichkeiten entlang eines Pfades miteinander multipliziert werden.

1.3. Die Zweite Pfadregel:
Die Wahrscheinlichkeit, dass ein bestimmtes Ereignis eintritt ergibt sich aus der Summe aller Elementarwahrscheinlichkeite, die dieses bestimmte Ereignis betreffen.

2. Zuordnung von Bäumen

2.1. Das Baumdiagramm a. ist das richtige, da b. unter anderem nicht der Verzweigungsregel entspricht.

2.2. Das Baumdiagramm b. ist das richtige, da bei a. nicht alle Ereignisse angegeben sind; es fehlt blau.

2.3. Das Baumdiagramm a. ist das richtige, da b. nicht die Reihenfolge berücksichtigt.

3. Zeichnen von leichten Baumdiagrammen

3.1. Der Manager hat folgende Möglichkeiten nach London zu gelangen:

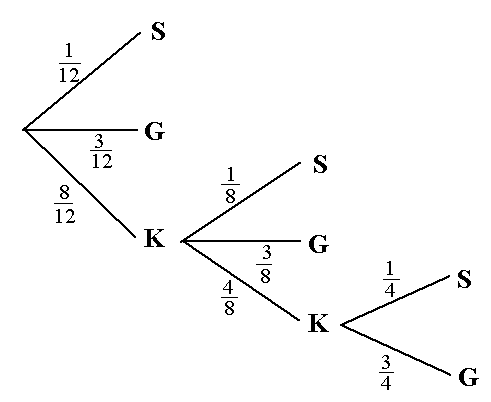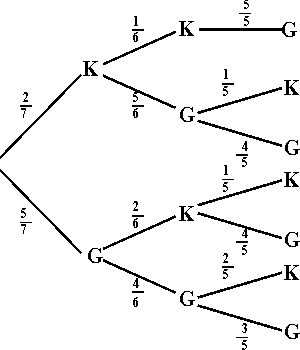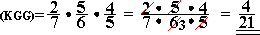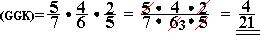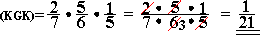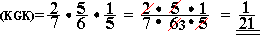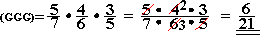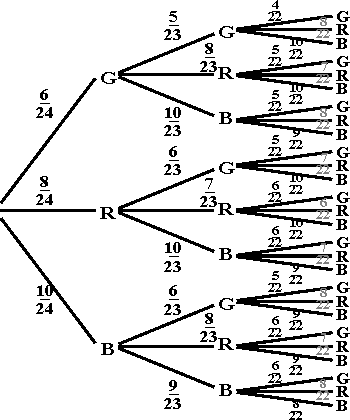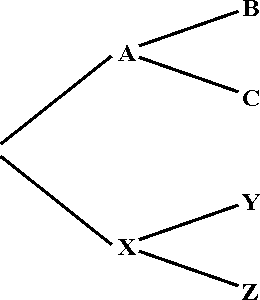
3.2. Durch bloses Raten ist die Holzkugel so zu finden:

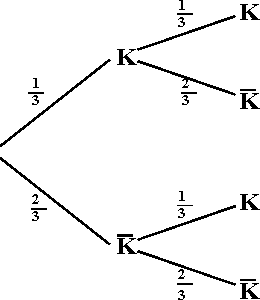
3.3. Den "Alten" bekommt er wie folgt:

       S = "besagter Spieler bekommt den Alten"
       G = "einer der 3 gegnerischen Spieler bekommt den Alten"
       K = "kein Spieler bekommt den Alten"

4.1. Baumdigramm; BOS Schüler im Schwimmbad mit folgenden Handtüchern:

4.2.1. P
4.2.2. P
4.2.3. P
4.2.4. P
4.2.5. P

5.1. Baumdiagramm des Urnen- Experiments

" / " heisst geteilt 5.3. Elementarereignisse
P({GGG})=10/1012
P({GGR})=20/1012
P({GGB})=25/1012
P({GRG})=20/1012
P({GRR})=28/1012
P({GRB})=40/1012
P({GBG})=25/1012
P({GBB})=40/1012
P({GBR})=45/1012

P({RGG})=20/1012
P({RGR})=28/1012
P({RGB})=40/1012
P({RRG})=28/1012
P({RRR})=28/1012
P({RRB})=70/1518
P({RBG})=40/1012
P({RBR})=70/1518
P({RBB})=60/1012

P({BGG})=25/1012
P({BGR})=40/1012
P({BGB})=45/1012
P({BRG})=40/1012
P({BRR})=70/1518
P({BRB})=60/1012
P({BBG})=45/1012
P({BBR})=60/1012
P({BBB})=60/1012

5.4.1. Mindestens einmal R.
P({GGR})=20/1012
P({GRG})=20/1012
P({GRR})=28/1012
P({GRB})=40/1012
P({GBR})=45/1012
P({RGG})=20/1012
P({RGR})=28/1012
P({RGB})=40/1012
P({RRG})=28/1012
P({RRR})=28/1012
P({RRB})=70/1518
P({RBG})=40/1012
P({RBR})=70/1518
P({RBB})=60/1012
P({BGR})=40/1012
P({BRG})=40/1012
P({BRR})=70/1518
P({BRB})=60/1012
P({BBR})=60/1012

P({min. 1x R})=0,204216 ca. 20 %

5.4.2. Höschtens einmal G.
P({GRR})=28/1012
P({GRB})=40/1012
P({GBB})=40/1012
P({GBR})=45/1012
P({RGR})=28/1012
P({RGB})=40/1012
P({RRG})=28/1012
P({RRR})=28/1012
P({RRB})=70/1518
P({RBG})=40/1012
P({RBR})=70/1518
P({RBB})=60/1012
P({BGR})=40/1012
P({BGB})=45/1012
P({BRG})=40/1012
P({BRR})=70/1518
P({BRB})=60/1012
P({BBG})=45/1012
P({BBR})=60/1012
P({BBB})=60/1012

P({max. 1x G})=0,8567193 ca. 86 %

5.4.3. Genau zweimal B.
P({GBB})=40/1012
P({RBB})=60/1012
P({BBG})=45/1012
P({BBR})=60/1012

P({2x B})=0,2025691 ca. 20 %