Lösung: P (X = 2) = B (10;
Gegeben: n = 10 ; p = ![]() ; k = 2
; k = 2
Lösung: P (X = 2) = B (10;![]() ;
2) =
;
2) = ![]() *
* ![]() 2
*
2
* ![]() 8
= 0,29071 => 29,1 %
8
= 0,29071 => 29,1 %
P (X ![]() 2)
=
2)
= ![]() B (10;
B (10;
![]() ;
i) = 0,77523 => 77,5 %
;
i) = 0,77523 => 77,5 %
Gegeben:
Wahrscheinlichkeit, dass -Teil A defekt ist: 0,01 -Teil B defekt
ist: 0,01
-Teil C defekt ist: 0,05 - Zusammenbaufehler: 0,02 ; n = 1000 ; X = Anzahl
der defekten Exemplare
Lösung:
q = P (Gerät nicht defekt) = 0,99 * 0,99 * 0,95 * 0,98 =
0,9124731 => gerundet: 0,91
p = P (Gerät defekt) = 1 - 0,91 = 0,09
E (X) = 1000 * 0,09 = 90
Var (X) = 90 * 0,91 = 81, 90 => ![]() = 9,05
= 9,05
Gegeben:
Wahrscheinlichkeit, dass: -Teil A defekt ist: 0,01 -Teil B defekt ist: 0,01
-Teil C defekt ist: 0,05 - Zusammenbaufehler: 0,02 ; n = 1000
Lösung:
q = 0,99 * 0,99 * 0,99 * 0,98 = 0,95 (gerundet)
p = 1 - 0,95 = 0,05
E (X) = 1000 * 0,05 = 50
eingesparte Reparaturkosten: (90 € * 100 €) - (50 € * 100 €)
= 4000 €
=> Aufpreis (höchstens) pro Bauteil C = 4000 € : 1000 Stück
= 4 €
Gegeben: µ = 5 = E (X) ; ![]() 2
= 3,75 = Var (X)
2
= 3,75 = Var (X)
Gesucht: n, p
Lösung:
µ = n * p = 5
Var (X) = 3,75 = n * p * q = 5q => q = 3,75 : 5 = 0,75
=> p = 1 - 0,75 = 0,25
=> n * 0,25 = 5 => n = 20
Lösung 3b:
P ( | X - µ | ![]() 2) = P (| X - 5|
2) = P (| X - 5| ![]() 2) = P ( X
2) = P ( X ![]() 3)
+ P ( X
3)
+ P ( X ![]() 7) = P ( X
7) = P ( X ![]() 3)
+ 1 - P ( X
3)
+ 1 - P ( X ![]() 6)
6)
= ![]() B (
20; 0,25; i) + 1 -
B (
20; 0,25; i) + 1 - ![]() B ( 20; 0,25; i) = 0,22516 + 0,21422 = 0,43938 => 43,9 %
B ( 20; 0,25; i) = 0,22516 + 0,21422 = 0,43938 => 43,9 %
P ( µ - ![]() <
X < µ +
<
X < µ + ![]() )
= P ( 5 - 1,94 < X < 5 + 1,94 )
)
= P ( 5 - 1,94 < X < 5 + 1,94 )
= P ( 3,06 < X < 6,94 )
= P ( X ![]() 6) - P ( X
6) - P ( X ![]() 3 ) =
3 ) = ![]() B ( 20; 0,25; i ) -
B ( 20; 0,25; i ) - ![]() B ( 20; 0,25; i )
B ( 20; 0,25; i )
= 0,78578 - 0,22516 = 0,56062 => 56,1 %
Gegeben: n = 200 ; p = 0,1 ; X = Melone mit Untergewicht
Lösung:
PA ( X ![]() 20
) =
20
) = ![]() B (
200; 0,1; i) = 0,55917 => 55,9 %
B (
200; 0,1; i) = 0,55917 => 55,9 %
PB ( 16 ![]() X
X
![]() 24
) = P ( X
24
) = P ( X ![]() 24 ) - P ( X
24 ) - P ( X ![]() 15
)
15
)
= ![]() B (
200; 0,1; i ) -
B (
200; 0,1; i ) - ![]() B ( 200; 0,1; i )
B ( 200; 0,1; i )
= 0,71203 => 71,2 %
PC = ( X > 24 ) = 1 - P ( X ![]() 24) = 0,14489 => 14,5 %
24) = 0,14489 => 14,5 %
Gegeben: n = 20; p = 0,1 ; X = Melone mit Untergewicht
Lösung:
P ( X > 3 ) = 1 - P ( X ![]() 3
)
3
)
= 1 - ![]() B ( 20; 0,1; i ) = 1 - 0,86705 = 0,13295 => 13,3 %
B ( 20; 0,1; i ) = 1 - 0,86705 = 0,13295 => 13,3 %
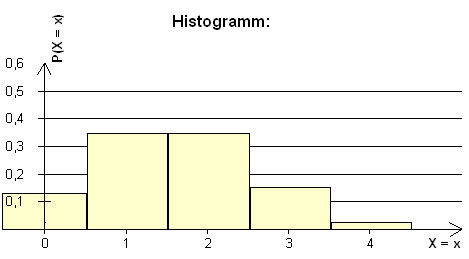
X ist eine B(4; 0,4)-verteilte Zufallsgröße (Werte aus dem Tafelwerk):
|
X = x
|
0
|
1
|
2
|
3
|
4
|
|
P (X = x)
|
0,1296
|
0,3456
|
0,3456
|
0,1536
|
0,0256
|
|
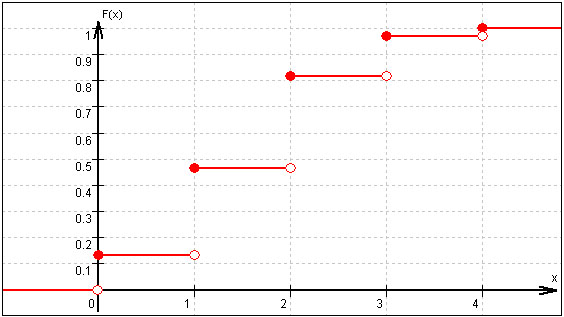
x < 0
|
0
|
1
|
2
|
3
|
4
|
|
|
F (x)
|
0
|
0,1296
|
0,4752
|
0,8208
|
0,9744
|
1
|
P(2 ![]() X
X ![]() 3)
= 0,3456 + 0,1536 = 0,4992
3)
= 0,3456 + 0,1536 = 0,4992
Um mindestens 8000 Mehreinnahmen zu erzielen, müsste der Händler
mindestens
100 (100 * 80 = 8000) Geräte des Typs H haben.
Es liegt eine B(200; 0,6)-verteilte Zufallsgröße vor :
P(X ![]() 100)
=
100)
= ![]() B (200;
0,6; i) = 1 -
B (200;
0,6; i) = 1 -![]() B
(200; 0,6; i) = 1 - 0,00168 = 0,99832
B
(200; 0,6; i) = 1 - 0,00168 = 0,99832
Erwartungswert für die Anzahl der Geräte des Typs H:
µ = 200 * 0,6 = 120
Mehreinnahmen: 120 * 80 = 9600 (in €)
Mehrausgaben: 200 * 40 = 8000 (in €)
Dem Händler blieben also trotz der Prüfkosten noch Mehreinnahmen in
Höhe von 1600€.
Es liegt eine Binomialverteilung mit n = 50 und p = 0,7 vor.
µ = n · p = 50 · 0,7 = 35
Var(X) = n · p · q = 35 · 0,3 = 10,5
![]() = 3,24
= 3,24
P (µ - ![]()
![]() X
X![]() µ +
µ + ![]() )
= P (31,76
)
= P (31,76 ![]() X
X
![]() 38,24) = P (32
38,24) = P (32 ![]() X
X
![]() 38)
38)
= F (38) - F (31) = 0,861 - 0,141 = 0,72
Mindestens 15 PCs sind genau dann frei, wenn höchstens 35 PCs belegt
sind.
P(X ![]() 35)
=
35)
= ![]() B (50;
0,7; i) = 0,553 = 55,3 %
B (50;
0,7; i) = 0,553 = 55,3 %
Es handelt sich um eine Bernoulli-Kette, da die Wahrscheinlichkeit für
das Eintreten von zwei Ereignissen gefragt ist:
P: "Pizza gewünscht" ; N: "Nudeln gewünscht"
Die Wahrscheinlichkeit für ein 8-Tupel der Form PPPPPPNN ist: 0,66
* 0,32
=> p = ![]() * 0,66 * 0,32
= 0,11757 , oder:
* 0,66 * 0,32
= 0,11757 , oder:
=> p = ![]() * 0,66 * 0,32
= 0,11757
* 0,66 * 0,32
= 0,11757
F: "Florian bekommt seine Gemüseplatte" = " von den 8 Personen
vor ihm nehmen höchstens 2 eine Gemüseplatte"
P (Gemüseplatte) = 1 - (0,6 + 0,3) = 0,1
P (F)= ![]() B (8; 0,1; i) = 0,96191
B (8; 0,1; i) = 0,96191