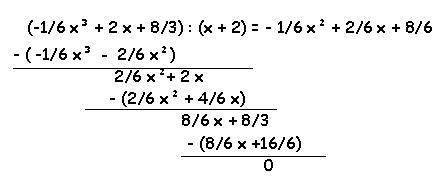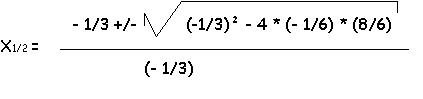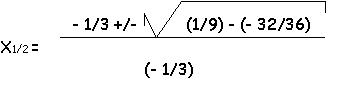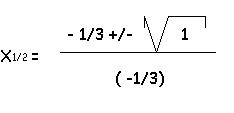Lösungen

 

Zur Lösung der Aufgabe 2a

Zur Lösung der Aufgabe 2b

Zur Lösung der Aufgabe 2c

1a)

f(x) = 7 * x³ + 3 * x + 5

f'(x) = 7 * 3 * x(3-1) + 3 * 1 * x(1-1) + 5 * 0 * x(0 -1)

f'(x) = 21 * x2 + 3

 

1b)

f(x) = x5 + 3 * x³ + 2 * x² - 8 * x

f'(x) = 1 * 5 * x(5-1) + 3 * 3 * x(3-1) + 2 * 2 * x(2-1) - 8 * 1 * x(1 -1)

f'(x) = 5 * x4 + 9 * x2 + 4 * x1 - 8

 

1c)

f(x) = - 0,5 * x4 + 2,5 * x³- 4 * x² + 1,5 * x - 3

f'(x) = - 0,5 * 4 * x(4-1) + 2,5 * 3 * x(3-1) - 4 * 2 * x(2-1) + 1,5 * 1 * x(1 -1) - 3 * 0 * x(0 -1)

f'(x) = - 2 * x3 + 7,5 * x2 - 8 * x1 + 1,5

 

Zurück zur Aufgabe

2a)

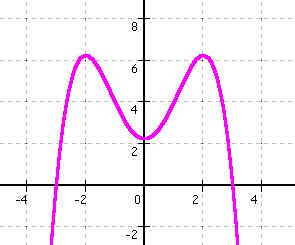
f(x) = - 0,25 * ( x4 - 8 * x²- 9)

Nullstellen:

f(x) = 0

0 = - 0,25 * ( x4 - 8 * x²- 9)

0 = x4 - 8 * x²- 9

 

Substitution: x² = z

0 = z²- 8 * z - 9

Mitternachtsformel:

 

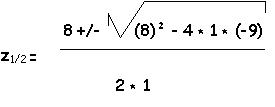
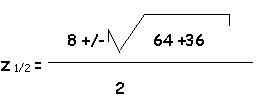
z1 = 9

 

 

 

 
 
x1/2 =
 

 

x1 = 3

x2 = -3

 

z2 = - 1

 

Das sich aus einer Zahl mit negativem Vorzeichen keine Wurzel ziehen lässt, gibt es keine weiteren Nullstellen !

 

Skizze

x1 = 3

x2 = -3

 

Extrempunkte:

1. Ableitung !

f(x) = - 0,25 * ( x4 - 8 * x²- 9)

f'(x) = - 0,25 * (1 * 4 * x(4-1) - 8 * 2 * x(2-1) - 9 * 0 * x(0-1))

f'(x) = - 0,25 * (4 * x3 - 16 * x)

f'(x) = 0

0 = - 0,25 * (4 * x3 - 16 * x)

0 = 4 * x3 - 16 * x

0 = x * (4 * x2 - 16) x1 = 0

  
0 = 4 * x2 - 16
  
16 = 4 * x2
 
4 = x2
 
x2 = 2
  
x3 = -2
  

Nachweis, um welche Art des Extrempunktes es sich handelt - per Monotonietabelle:

f'(x) = - 0,25 * (4 * x3 - 16 * x)

 

 

 
x <
-2
< x <
0
< x <
2
< x
f'(x)

f'(-3) =

- 0,25 *

(4 * (-3)3

- 16 * (-3))

=

15
f'(x) = 0

f'(-1) =

- 0,25 *

(4 * (-1)3

- 16 * (-1))

=

- 3
f'(x) = 0

f'(1) =

- 0,25 *

(4 * (1)3

- 16 * (1))

=

3
f'(x) = 0
f'(3) =

- 0,25 *

(4 * (3)3

- 16 * (3))

=

- 15

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

neg. Vor-zeichen

(-)

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

neg.Vor-zeichen

(-)

 

 

 

 

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

 

 

 

 

 

 

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
HOP
handelt.


 
Daran kann man
erkennen, dass es sich
um einen:
TIP
handelt.

 

 
Daran kann man
erkennen, dass es sich
um einen:
HOP
handelt.

 


 

Lage der Extrempunkte:

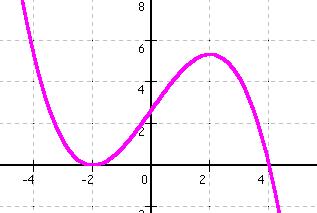
f(x) = - 0,25 * (x4 - 8 * x²- 9)

f(-2) = - 0,25 * ( (-2)4 - 8 * (-2)²- 9) = 6,25 HOP bei ( - 2/6,25 )

f(0) = - 0,25 * ((0)4 - 8 * (0)²- 9) = 2,25 TIP bei ( 0/2,25 )

f(2) = - 0,25 * ( (2)4 - 8 * (2)²- 9) = 6,25 HOP bei ( 2/6,25 )

 

 

 

 

 

2b)

f(x) = 1/6 * ( - x³ + 12 * x + 16)

Nullstellen:

f(x) = 0

0 = 1/6 * ( - x³ + 12 * x + 16)

0 = - x³ + 12 * x + 16

 

Ausprobieren !

f(0) = 1/6 * ( - (0)³ + 12 * (0) + 16) = 1/6 * 16 = 8/3 ! keine Nullstelle !

f(-2) = 1/6 * ( - (-2)³ + 12 * (-2) + 16) = 1/6 * ( 8 - 24 + 16) = 1/6 * 0 = 0 ! eine Nullstelle !

 

Polynomdivision !

[ 1/6 * (- x³ + 12 x + 16 )]

= (- 1/6 x³ + 2 x + 8/3)
 

 

 

0 = - 1/6 x² + 2/6 x+ 8/6

 

Mitternachtsformel !

 

 

x1 = - 2

x2 = 4

Skizze !

 

 

 

Extrempunkte:

1. Ableitung !

f(x) = 1/6 * ( - x³ + 12 * x + 16)

f'(x) = 1/6 * ( -1 * 3 * x(3-1) + 12 * 1 * x(1-1) + 16 * 0 * x(0-1))

f'(x) = 1/6 * (- 3 * x² + 12)

f'(x) = 0

0 = 1/6 * (- 3 * x² + 12)

0 = - 3 * x² + 12

- 12 = - 3 * x²

x² = 4

x1 = 2

x2 = - 2

Nachweis, um welche Art des Extrempunktes es sich handelt - per Monotonietabelle:

f'(x) = 1/6 * (- 3 * x² + 12)

 

 

 
x <
-2
< x <
2
< x
f'(x)

f'(-3) =

1/6 * (- 3 * (- 3)² + 12)

=

- 5/2
f'(x) = 0

f'(0) =

1/6 * (- 3 * (0)² + 12)

=

2
f'(x) = 0
f'(3) =

1/6 * (- 3 * (3)² + 12)

=

- 5/2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

das heißt:

der Wert von f' hat ein

neg. Vor-zeichen

(-)

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

neg.Vor-zeichen

(-)

 

 

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

 

 

 

 

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
TIP
handelt.


 

 
Daran kann man
erkennen, dass es sich
um einen:
HOP
handelt.


 

 

Lage der Extrempunkte:

f(x) = 1/6 * ( - x³ + 12 * x + 16)

f(-2) = 1/6 * ( -(- 2)³ + 12 * (- 2) + 16) = 0 TIP bei ( - 2/0)

f(2) = = 1/6 * ( -(2)³ + 12 * (2) + 16) = 16/3 HOP bei ( 2/5,33 )

 

 

 

2c)

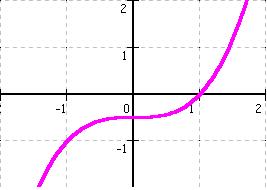
f(x) = 0,5 * x³ - 0,5

Nullstellen:

f(x) = 0

0 = 0,5 * x³ - 0,5

0,5 = 0,5 * x³

x³ = 1 , also x = 1

Skizze !

Extrempunkte:

1. Ableitung !

f(x) = 0,5 * x³ - 0,5

f'(x) = 0,5 * 3 * x(3-1) - 0,5 * 0 * x(0-1)

f'(x) = 1,5 * x²

f'(x) = 0

0 = 1,5 * x²

0 = x²

x = 0 doppelte Nullstelle in f'daraus folgt: Terrassenpunkt!

Nachweis, um welche Art von Punkt es sich handelt - per Monotonietabelle:

 

 
x <
0
< x
f'(x)

f'(-1) =

1,5 * (-1)²

=

1,5
f'(x) = 0

f'(1) =

1,5 * (1)²

=

1,5

 

 

 

 

 

 

 

 

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich weiter steigt

 

 

 

 

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
TEP
handelt.


 

Lage des Punktes:

f(x) = 0,5 * x³ - 0,5

f(0) = 0,5 * (0)³ - 0,5 = - 0,5 TEP bei ( 0/- 0,5)

 

zurück zur Aufgabe

Zurück zum Hauptmenü