Lösungen

 

Zur Lösung der Aufgabe 2a

Zur Lösung der Aufgabe 2b

Zur Lösung der Aufgabe 2c

 

1a)

f(x) = - 5 * x3 + 2 * x2 - 1,5

erst die 1. Ableitung:

f'(x) = - 5 * 3 * x(3-1) + 2 * 2 * x(2-1) - 1,5 * 0 * x(0 -1)

f'(x) = - 15 * x2 + 4 * x

dann die 2. Ableitung, indem die 1. Ableitung abgeleitet wird:

f'(x) = - 15 * x2 + 4 * x

f''(x) = - 15 * 2 * x(2-1) + 4 * 1 * x(1-1) Wichtig ist hierbei, dass die 2. Ableitung f''(x) heißt !

f''(x) = - 30 * x + 4

 

 

1b)

f(x) = 6 * x4 - 9 * x3 - 2 * x2 + 3

erst die 1. Ableitung:

f'(x) = 6 * 4 * x(4-1) - 9 * 3 * x(3-1) - 2 * 2 * x(2 -1) + 3 * 0 * x(0-1)

f'(x) = 24 * x3 - 27 * x2 - 4 * x

 

dann die 2. Ableitung, indem die 1. Ableitung abgeleitet wird:

f'(x) = 24 * x3 - 27 * x2 - 4 * x

f''(x) = 24 * 3 * x(3-1) - 27 * 2 * x(2-1) - 4 * 1 * x(1-1)

f''(x) = 72 * x2 - 54 * x - 4

 

 

 

1c)

f(x) = - 5,5 * x2 + 7 * x + 10

erst die 1. Ableitung:

f'(x) = -5,5 * 2 * x(2-1) + 7 * 1 * x(1-1) + 10 * 0 * x(0 -1)

f'(x) = - 11 * x + 7

dann die 2. Ableitung, indem die 1. Ableitung abgeleitet wird:

f'(x) = - 11 * x + 7

f''(x) = - 11 * 1 * x(1-1) + 7 * 0 * x(0-1)

f''(x) = - 11

Da der Graph jedoch eine Parabel ist, existiert gar kein Wendepunkt !

Beweis: Zum Errechnen des Wendepunktes muß man die 2. Ableitung gleich Null setzen, jedoch würde in diesem Fall die falsche Aussage 0 = - 11 gemacht werden und sich kein Wendepunkt errechnen lassen !

 

 

Zurück zur Aufgabe

 

2a)

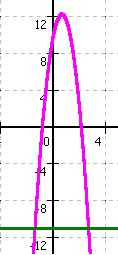f(x) = 0,5 * x3 - 3 * x2 + 5 * x - 4

Berechnung der Extrempunkte mittels der 1. Ableitung !

f'(x) = 0,5 * 3 * x(3-1) - 3 * 2 * x(2-1) + 5 * 1 * x(1 -1) - 4 * 0 * x(0 -1)

f'(x) = 1,5 * x2 - 6 * x + 5

0 = 1,5 * x2 - 6 * x + 5

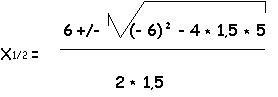
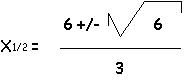
x1 = 2,8

x2 = 1,2

Art der Extrempunkte mittels Monotonietabelle !

 

 
x <
1,2
< x <
2,8
< x
f'(x)

f'(1) =

1,5 * (1)2 - 6 * (1) + 5

=

0,5
f'(x) = 0

f'(2) =

1,5 * (2)2 - 6 * (2) + 5

=

- 1
f'(x) = 0
f'(3) =

1,5 * (3)2 - 6 * (3) + 5

=

0,5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

das heißt:

der Wert von f'

hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

neg. Vor-zeichen

(-)

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

 

 

 

 

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
HOP
handelt.


 
Daran kann man
erkennen, dass es sich
um einen:
TIP
handelt.


 

 

Lage der Extrempunkte, indem die x-Werte der Extrema in f(x) eingesetzt werden !

f(x) = 0,5 * x3 - 3 * x2 + 5 * x - 4

f(1,2) = 0,5 * (1,2)3 - 3 * (1,2)2 + 5 * x - 4 = - 1,45

f(2,8) = 0,5 * (2,8)3 - 3 * (2,8)2 + 5 * x - 4 = - 2,5

 

 

Den Wendepunkt mittels 2. Ableitung errechnen !

f'(x) = 1,5 * x2 - 6 * x + 5

f''(x) = 1,5 * 2 * x(2-1) - 6 * 1 * x(1-1) + 5 * 0 * x(0 -1)

f''(x) = 3 * x - 6

Nullstellen der 2. Ableitung = WEP !

0 = 3 * x - 6

6 = 3 * x

x = 2

Nachweis, dass es sich um einen WEP handelt - mittels Krümmungstabelle !

 

 
x <
2
< x
f''(x)

f''(1) = 3 * (1) - 6

= - 3
f''(x) = 0

f''(3) = 3 * (3) - 6

= 3

 

 

 

 

 

 

das heißt:

der Wert von f'' hat ein neg. Vorzeichen

(-)

 

 

das heißt:

der Wert von f'' hat ein pos. Vorzeichen

(+)

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich rechtsgekrümmt ist

 

 

das heißt:

dass die Funktion in diesem Bereich linksgekrümmt ist

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
WEP
handelt.

 

 

Koordinaten des Wendepunkts mittels f(x) errechnen !

f(x) = 0,5 * x3 - 3 * x2 + 5 * x - 4

f(2) = 0,5 * (2)3 - 3 * (2)2 + 5 * x - 4 = - 2

Skizze !

 

 

Zurück zur Aufgabe

 

2b)

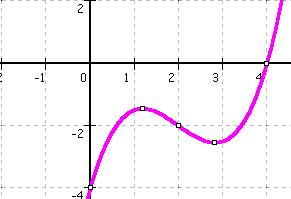f(x) = - 1/8 * x4 + 5/4 * x3 - 3 * x2 + 23/8

Berechnung der Extrempunkte mittels der 1. Ableitung !

f'(x) = - 1/8 * 4 * x(4-1) + 5/4 * 3 * x(3-1) - 3 * 2 * x(2 -1) + 23/8 * 0 * x(0 -1)

f'(x) = - 1/2 * x3 + 15/4 * x2 - 6 * x

0 = - 1/2 * x3 + 15/4 * x2 - 6 * x

0 = x * (-1/2 * x2 + 15/4 * x- 6)

x1 = 0
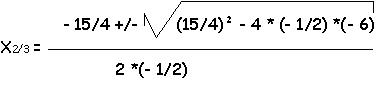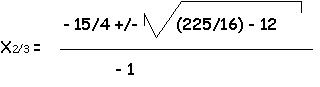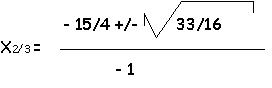x2 = 2,3
x3 = 5,2

 

Art der Extrempunkte mittels Monotonietabelle !

 

 
x <
0
< x <
2,3
< x <
5,2
< x
f'(x)

f'(- 1) =

- 1/2 * (-1)3 + 15/4 * (-1)2 - 6 * (-1)

=

41/4
f'(x) = 0

f'(1) =

- 1/2 * (1)3 +15/4 * (1)2 - 6 * (1)

=

- 11/4
f'(x) = 0

f'(3) =

- 1/2 * (3)3 + 15/4 * (3)2 - 6 * (3)

=

9/4
f'(x) = 0

f'(6) =

- 1/2 * (6)3 + 15/4 * (6)2 - 6 * (6)

=

- 9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

neg. Vor-zeichen

(-)

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

neg. Vor-zeichen

(-)

 

 

 

 

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

 

 

 

 

 

 

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
HOP
handelt.


 
Daran kann man
erkennen, dass es sich
um einen:
TIP
handelt.

 

 
Daran kann man
erkennen, dass es sich
um einen:
HOP
handelt.


 

 

Lage der Extrempunkte, indem die x-Werte der Extrema in f(x) eingesetzt werden !

f(x) = - 1/8 * x4 + 5/4 * x3 - 3 * x2 + 23/8

f(0) = - 1/8 * (0)4 + 5/4 * (0)3 - 3 * (0) 2 + 23/8 = 23/8

f(2,3) = - 1/8 * (2,3)4 + 5/4 * (2,3)3 - 3 * (2,3)2 + 23/8 = - 1,3

f(5,2) = - 1/8 * (5,2)4 + 5/4 * (5,2)3 - 3 * x(5,2)2 + 23/8 = 6,1

 

 

Die Wendepunkte mittels 2. Ableitung errechnen !

f'(x) = - 1/2 * x3 + 15/4 * x2 - 6 * x

f''(x) = - 1/2 * 3 * x(3-1) + 15/4* 2 * x(2-1) - 6 * 1 * x(1 -1)

f''(x) = - 3/2 * x2 + 15/2 * x - 6

Nullstellen der 2. Ableitung = WEP !

0 = - 3/2 * x2 + 15/2 * x - 6

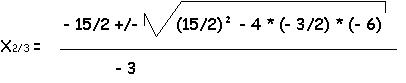
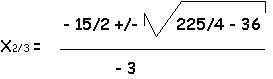
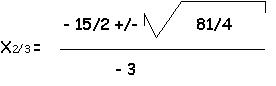
x1 = 1

x2 = 4

Nachweis, dass es sich um WEP handelt - mittels Krümmungstabelle !

 

 
x <
1
< x<
4
< x
f''(x)
f''(0) = - 3/2 * (0)2 + 15/2 * (0) - 6 = - 6
f''(x) = 0
f''(2) = - 3/2 * (2)2 + 15/2 * (2) - 6 = 3
f''(x) = 0
f''(5) = - 3/2 * (5)2 + 15/2 * (5) - 6 = - 6

 

 

 

 

 

 

 

 

das heißt:

der Wert von f'' hat ein neg. Vorzeichen

(-)

 

 

das heißt:

der Wert von f'' hat ein pos. Vorzeichen

(+)

 

 

das heißt:

der Wert von f'' hat ein neg. Vorzeichen

(-)

 

 

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich rechtsgekrümmt ist

 

 

das heißt:

dass die Funktion in diesem Bereich linksgekrümmt ist

 

 

das heißt:

dass die Funktion in diesem Bereich rechtsgekrümmt ist

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
WEP
handelt.

 

 
Daran kann man
erkennen, dass es sich
um einen:
WEP
handelt.


 

 

Koordinaten der Wendepunkte mittels f(x) errechnen !

f(x) = - 1/8 * x4 + 5/4 * x3 - 3 * x2 + 23/8

f(1) = - 1/8 * (1)4 + 5/4 * (1)3 - 3 * (1)2 + 23/8 = 1

f(4) = - 1/8 * (4)4 + 5/4 * (4)3 - 3 * (4)2 + 23/8 = 23/8

Skizze !

 

Zurück zur Aufgabe

 

2c)

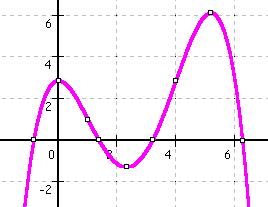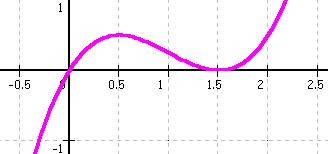
f(x) = x3 - 3 * x2 + 2,25 * x

Berechnung der Extrempunkte mittels der 1. Ableitung !

f'(x) = 1 * 3 * x(3-1) - 3 * 2 * x(2-1) + 2,25 * 1 * x(1 -1)

f'(x) =3 * x 2 - 6 * x + 2,25

0 = 3 * x2 - 6 * x + 2,25

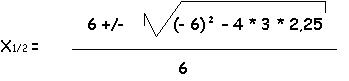
x1 = 1,5

x2 = 0,5

 

Art der Extrempunkte mittels Monotonietabelle !

 

 
x <
0,5
< x <
1,5
< x
f'(x)

f'(0) =

3 * (0)2 - 6 * (0) + 2,25

=

2,25
f'(x) = 0

f'(1) =

3 * (1)2 - 6 * (1) + 2,25

=

- 0,75
f'(x) = 0
f'(2) =

3 * (2)2 - 6 * (2) + 2,25

=

2,25

 

 

 

 

 

 

 

 

 

 

 

 

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

das heißt:

der Wert von f' hat ein

neg. Vor-zeichen

(-)

 

 

das heißt:

der Wert von f' hat ein

pos. Vor-zeichen

(+)

 

 

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

das heißt:

dass die Funktion in diesem Bereich fällt

 

 

das heißt:

dass die Funktion in diesem Bereich steigt

 

 

 

 

 

 

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
HOP
handelt.

 
Daran kann man
erkennen, dass es sich
um einen:
TIP
handelt.

 

 

Lage der Extrempunkte, indem die x-Werte der Extrema in f(x) eingesetzt werden !

f(x) = x3 - 3 * x2 + 2,25 * x

f(0,5) = (0,5)3 - 3 * (0,5)2 + 2,25 * (0,5) = 0,5

f(1,5) = (1,5)3 - 3 * (1,5)2 + 2,25 * (1,5) = 0

 

 

Den Wendepunkt mittels 2. Ableitung errechnen !

f'(x) = 3 * x 2 - 6 * x + 2,25

f''(x) = 3 * 2 * x(2-1) - 6 * 1 * x(1-1) + 2,25 * 0 * x(0 -1)

f''(x) = 6 * x - 6

Nullstellen der 2. Ableitung = WEP !

0 = 6 * x - 6

6 = 6 * x

x = 1

Nachweis, dass es sich um einen WEP handelt - mittels Krümmungstabelle !

 

 
x <
1
< x
f''(x)

f''(0) = 6 * (0) - 6

= - 6
f''(x) = 0

f''(2) = 6 * (2) - 6

= 6

 

 

 

 

 

 

das heißt:

der Wert von f'' hat ein neg. Vorzeichen

(-)

 

 

das heißt:

der Wert von f'' hat ein pos. Vorzeichen

(+)

 

 

 

 

 

 

das heißt:

dass die Funktion in diesem Bereich rechtsgekrümmt ist

 

 

das heißt:

dass die Funktion in diesem Bereich linksgekrümmt ist

 

 

 

 
Daran kann man
erkennen, dass es sich
um einen:
WEP
handelt.


 

 

Koordinaten des Wendepunkts mittels f(x) errechnen !

f(x) = x3 - 3 * x2 + 2,25 * x

f(1) = (1)3 - 3 * (1)2 + 2,25 * (1) = 0,25

Skizze !

 

Zurück zur Aufgabe

Zurück zum Hauptmenü