Lösungen quadratische Gleichungen

1)

a) x²–5x+3 = –3 | +3 alles auf eine Seite stellen

x²–5x+6 = 0

D = (–5)² – 4•1•6 Diskriminante aufstellen

D = 1 > 0 →    2 Lösungen

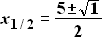Lösungen ausrechnen

x₁ = 2 x₂ = 3

b) x²+24x+36 = 12x | –12x alles auf eine Seite stellen

x²+12x+36 = 0

D = 12²–4•1•36 Diskriminante aufstellen

D = 144 – 144

D = 0 → 1 doppelte Lösung

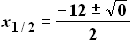
x_1/2 = –6

2)

(x–7)²+(x–1)² = 15 ausmultiplizieren mit binomischer Formel

x²–14x+49+x²–2x+1 = 15 | –15

2x²–16x+35 = 0

D = (–16)²–4•2•35 Diskriminante aufstellen

D = 256–280

D = –24 → keine Lösungen

3)

Wir verwenden x und y für die Zahlen. Das Gleichungssystem x+y = 10, x•y = 11 löst man, indem man die erste Gleichung nach y auflöst

( y = 10–x ) und in die zweite einsetzt:

x•(10–x) = 11

10x–x² = 11

x²–10x+11 = 0

D = (–10)²–4•1•11 Diskriminante aufstellen

D = 100 – 44

D = 56

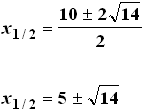Lösungen berechnen

Das heißt:

Ist x = 5+√14, so ist y = 10–x = 5–√14

Ist x = 5–√14, so ist y = 10–x = 5+√14